全一卷
1.下列说法正确的个数是( )
①-2022的相反数是2022;②-2022的绝对值是2022;③ 的倒数是2022.
的倒数是2022.
①-2022的相反数是2022;②-2022的绝对值是2022;③
 的倒数是2022.
的倒数是2022.| A.3 | B.2 | C.1 | D.0 |
2.我市围绕创建全国文明典范城市、传承弘扬屈原文化,组织开展了“喜迎二十大、永远跟党走、奋进新征程”等系列活动.在2022年“书香宜昌·全民读书月”暨“首届屈原文化月”活动中,100多个社区图书室、山区学校、农家书屋、“护苗”工作站共获赠了价值100万元的红色经典读物、屈原文化优秀读物和智能书柜.“100万”用科学记数法表示为( )
A. | B. | C. | D. |
3.下列运算错误 的是( )
A. | B. | C. | D. |
4.五一小长假,小华和家人到公园游玩.湖边有大小两种游船.小华发现1艘大船与2艘小船一次共可以满载游客32人,2艘大船与1艘小船一次共可以满载游客46人.则1艘大船与1艘小船一次共可以满载游客的人数为( )
| A.30 | B.26 | C.24 | D.22 |
5.如图是小强散步过程中所走的路程 (单位:
(单位: )与步行时间
)与步行时间 (单位:
(单位: )的函数图象.其中有一时间段小强是匀速步行的.则这一时间段小强的步行速度为( )
)的函数图象.其中有一时间段小强是匀速步行的.则这一时间段小强的步行速度为( )

 (单位:
(单位: )与步行时间
)与步行时间 (单位:
(单位: )的函数图象.其中有一时间段小强是匀速步行的.则这一时间段小强的步行速度为( )
)的函数图象.其中有一时间段小强是匀速步行的.则这一时间段小强的步行速度为( )
A. | B. | C. | D. |
6.将四个数字看作一个图形,则下列四个图形中,是中心对称图形的是( )
A. | B. | C. | D. |
7.已知经过闭合电路的电流 (单位:
(单位: )与电路的电阻
)与电路的电阻 (单位:
(单位: )是反比例函数关系.根据下表判断
)是反比例函数关系.根据下表判断 和
和 的大小关系为( )
的大小关系为( )
 (单位:
(单位: )与电路的电阻
)与电路的电阻 (单位:
(单位: )是反比例函数关系.根据下表判断
)是反比例函数关系.根据下表判断 和
和 的大小关系为( )
的大小关系为( )
| 5 | … |
| … | … | … |
| … | 1 |
| 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 |
A. | B. | C. | D. |
8.如图,在 中,分别以点
中,分别以点 和点
和点 为圆心,大于
为圆心,大于 长为半径画弧,两弧相交于点
长为半径画弧,两弧相交于点 ,
, .作直线
.作直线 ,交
,交 于点
于点 ,交
,交 于点
于点 ,连接
,连接 .若
.若 ,
, ,
, ,则
,则 的周长为( )
的周长为( )

 中,分别以点
中,分别以点 和点
和点 为圆心,大于
为圆心,大于 长为半径画弧,两弧相交于点
长为半径画弧,两弧相交于点 ,
, .作直线
.作直线 ,交
,交 于点
于点 ,交
,交 于点
于点 ,连接
,连接 .若
.若 ,
, ,
, ,则
,则 的周长为( )
的周长为( )
| A.25 | B.22 | C.19 | D.18 |
9.如图,四边形 内接于
内接于 ,连接
,连接 ,
, ,
, ,若
,若 ,则
,则 ( )
( )

 内接于
内接于 ,连接
,连接 ,
, ,
, ,若
,若 ,则
,则 ( )
( )
A. | B. | C. | D. |
10.如图是一个教室平面示意图,我们把小刚的座位“第1列第3排”记为 .若小丽的座位为
.若小丽的座位为 ,以下四个座位中,与小丽相邻且能比较方便地讨论交流的同学的座位是( )
,以下四个座位中,与小丽相邻且能比较方便地讨论交流的同学的座位是( )

 .若小丽的座位为
.若小丽的座位为 ,以下四个座位中,与小丽相邻且能比较方便地讨论交流的同学的座位是( )
,以下四个座位中,与小丽相邻且能比较方便地讨论交流的同学的座位是( )
A. | B. | C. | D. |
11.某校团支部组织部分共青团员开展学雷锋志愿者服务活动,每个志愿者都可以从以下三个项目中任选一项参加:①敬老院做义工;②文化广场地面保洁;③路口文明岗值勤.则小明和小慧选择参加同一项目的概率是( )
A. | B. | C. | D. |
12.如图,点 ,
, ,
, 都在方格纸的格点上,
都在方格纸的格点上, 绕点
绕点 顺时针方向旋转
顺时针方向旋转 后得到
后得到 ,则点
,则点 运动的路径
运动的路径 的长为
的长为______ .

 ,
, ,
, 都在方格纸的格点上,
都在方格纸的格点上, 绕点
绕点 顺时针方向旋转
顺时针方向旋转 后得到
后得到 ,则点
,则点 运动的路径
运动的路径 的长为
的长为
13.如图, 岛在A岛的北偏东
岛在A岛的北偏东 方向,
方向, 岛在
岛在 岛的北偏西
岛的北偏西 方向,则
方向,则 的大小是
的大小是_____ .

 岛在A岛的北偏东
岛在A岛的北偏东 方向,
方向, 岛在
岛在 岛的北偏西
岛的北偏西 方向,则
方向,则 的大小是
的大小是
14.如图,在矩形 中,
中, 是边
是边 上一点,
上一点, ,
, 分别是
分别是 ,
, 的中点,连接
的中点,连接 ,
, ,
, ,若
,若 ,
, ,
, ,矩形
,矩形 的面积为
的面积为________ .

 中,
中, 是边
是边 上一点,
上一点, ,
, 分别是
分别是 ,
, 的中点,连接
的中点,连接 ,
, ,
, ,若
,若 ,
, ,
, ,矩形
,矩形 的面积为
的面积为
15.解不等式 ,并在数轴上表示解集.
,并在数轴上表示解集.

 ,并在数轴上表示解集.
,并在数轴上表示解集.
16.某校为响应“传承屈原文化·弘扬屈原精神”主题阅读倡议,进一步深化全民阅读和书香宜昌建设,随机抽取了八年级若干名学生,对“双减”后学生周末课外阅读时间进行了调查.根据收集到的数据,整理后得到下列不完整的图表:

请你根据图表中提供的信息,解答下面的问题:
(1)扇形统计图中,120~150分钟时间段对应扇形的圆心角的度数是_______; _______;样本数据的中位数位于________~________分钟时间段;
_______;样本数据的中位数位于________~________分钟时间段;
(2)请将表格补充完整;
(3)请通过计算估计该校八年级学生周末课外平均阅读时间.
时间段/分钟 |
|
|
|
|
组中值 | 75 | 105 | 135 | |
频数/人 | 6 | 20 | 4 |

请你根据图表中提供的信息,解答下面的问题:
(1)扇形统计图中,120~150分钟时间段对应扇形的圆心角的度数是_______;
 _______;样本数据的中位数位于________~________分钟时间段;
_______;样本数据的中位数位于________~________分钟时间段;(2)请将表格补充完整;
(3)请通过计算估计该校八年级学生周末课外平均阅读时间.
17.石拱桥是我国古代人民勤劳和智慧的结晶(如图1),隋代建造的赵州桥距今约有1400年历史,是我国古代石拱桥的代表.如图2是根据某石拱桥的实物图画出的几何图形,桥的主桥拱是圆弧形,表示为 .桥的跨度(弧所对的弦长)
.桥的跨度(弧所对的弦长) ,设
,设 所在圆的圆心为
所在圆的圆心为 ,半径
,半径 ,垂足为
,垂足为 .拱高(弧的中点到弦的距离)
.拱高(弧的中点到弦的距离) .连接
.连接 .
.

(1)直接判断 与
与 的数量关系;
的数量关系;
(2)求这座石拱桥主桥拱的半径(精确到 ).
).
 .桥的跨度(弧所对的弦长)
.桥的跨度(弧所对的弦长) ,设
,设 所在圆的圆心为
所在圆的圆心为 ,半径
,半径 ,垂足为
,垂足为 .拱高(弧的中点到弦的距离)
.拱高(弧的中点到弦的距离) .连接
.连接 .
.
(1)直接判断
 与
与 的数量关系;
的数量关系;(2)求这座石拱桥主桥拱的半径(精确到
 ).
).18.知识小提示:要想使人安全地攀上斜靠在墙面上的梯子的顶端,梯子与地面所成的角 一般要满足
一般要满足 .如图,现有一架长
.如图,现有一架长 的梯子
的梯子 斜靠在一竖直的墙
斜靠在一竖直的墙 上.
上.

(1)当人安全使用这架梯子时,求梯子顶端 与地面距离的最大值;
与地面距离的最大值;
(2)当梯子底端 距离墙面
距离墙面 时,计算
时,计算 等于多少度?并判断此时人是否能安全使用这架梯子?
等于多少度?并判断此时人是否能安全使用这架梯子?
(参考数据: ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, )
)
 一般要满足
一般要满足 .如图,现有一架长
.如图,现有一架长 的梯子
的梯子 斜靠在一竖直的墙
斜靠在一竖直的墙 上.
上.
(1)当人安全使用这架梯子时,求梯子顶端
 与地面距离的最大值;
与地面距离的最大值;(2)当梯子底端
 距离墙面
距离墙面 时,计算
时,计算 等于多少度?并判断此时人是否能安全使用这架梯子?
等于多少度?并判断此时人是否能安全使用这架梯子?(参考数据:
 ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, )
)19.已知菱形 中,
中, 是边
是边 的中点,
的中点, 是边
是边 上一点.
上一点.
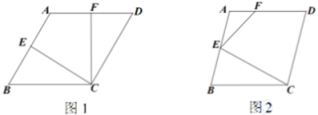
(1)如图1,连接 ,
, .
.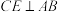 ,
, .
.
①求证: ;
;
②若 ,求
,求 的长;
的长;
(2)如图2,连接 ,
, .若
.若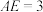 ,
, ,求
,求 的长.
的长.
 中,
中, 是边
是边 的中点,
的中点, 是边
是边 上一点.
上一点.
(1)如图1,连接
 ,
, .
.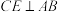 ,
, .
.①求证:
 ;
;②若
 ,求
,求 的长;
的长;(2)如图2,连接
 ,
, .若
.若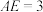 ,
, ,求
,求 的长.
的长.20.某造纸厂为节约木材,实现企业绿色低碳发展,通过技术改造升级,使再生纸项目的生产规模不断扩大.该厂3,4月份共生产再生纸800吨,其中4月份再生纸产量是3月份的2倍少100吨.
(1)求4月份再生纸的产量;
(2)若4月份每吨再生纸的利润为1000元,5月份再生纸产量比上月增加 .5月份每吨再生纸的利润比上月增加
.5月份每吨再生纸的利润比上月增加 ,则5月份再生纸项目月利润达到66万元.求
,则5月份再生纸项目月利润达到66万元.求 的值;
的值;
(3)若4月份每吨再生纸的利润为1200元,4至6月每吨再生纸利润的月平均增长率与6月份再生纸产量比上月增长的百分数相同,6月份再生纸项目月利润比上月增加了 .求6月份每吨再生纸的利润是多少元?
.求6月份每吨再生纸的利润是多少元?
(1)求4月份再生纸的产量;
(2)若4月份每吨再生纸的利润为1000元,5月份再生纸产量比上月增加
 .5月份每吨再生纸的利润比上月增加
.5月份每吨再生纸的利润比上月增加 ,则5月份再生纸项目月利润达到66万元.求
,则5月份再生纸项目月利润达到66万元.求 的值;
的值;(3)若4月份每吨再生纸的利润为1200元,4至6月每吨再生纸利润的月平均增长率与6月份再生纸产量比上月增长的百分数相同,6月份再生纸项目月利润比上月增加了
 .求6月份每吨再生纸的利润是多少元?
.求6月份每吨再生纸的利润是多少元?21.已知,在 中,
中,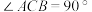 ,
,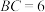 ,以
,以 为直径的
为直径的 与
与 交于点
交于点 ,将
,将 沿射线
沿射线 平移得到
平移得到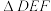 ,连接
,连接 .
.
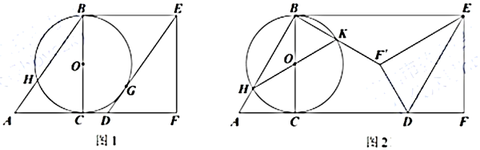
(1)如图1, 与
与 相切于点
相切于点 .
.
①求证: ;
;
②求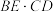 的值;
的值;
(2)如图2,延长 与
与 交于点
交于点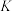 ,将
,将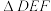 沿
沿 折叠,点
折叠,点 的对称点
的对称点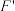 恰好落在射线
恰好落在射线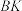 上.
上.
①求证: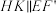 ;
;
②若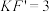 ,求
,求 的长.
的长.
 中,
中,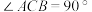 ,
,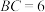 ,以
,以 为直径的
为直径的 与
与 交于点
交于点 ,将
,将 沿射线
沿射线 平移得到
平移得到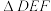 ,连接
,连接 .
.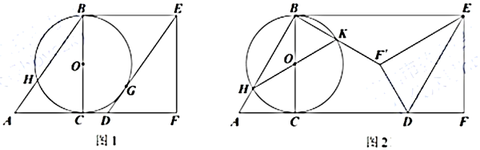
(1)如图1,
 与
与 相切于点
相切于点 .
.①求证:
 ;
;②求
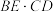 的值;
的值;(2)如图2,延长
 与
与 交于点
交于点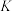 ,将
,将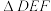 沿
沿 折叠,点
折叠,点 的对称点
的对称点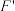 恰好落在射线
恰好落在射线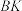 上.
上.①求证:
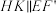 ;
;②若
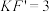 ,求
,求 的长.
的长.22.已知抛物线 与
与 轴交于
轴交于 ,
, 两点,与
两点,与 轴交于点
轴交于点 .直线
.直线 由直线
由直线 平移得到,与
平移得到,与 轴交于点
轴交于点 .四边形
.四边形 的四个顶点的坐标分别为
的四个顶点的坐标分别为 ,
, ,
, ,
, .
.

(1)填空: ______,
______, ______;
______;
(2)若点 在第二象限,直线
在第二象限,直线 与经过点
与经过点 的双曲线
的双曲线 有且只有一个交点,求
有且只有一个交点,求 的最大值;
的最大值;
(3)当直线 与四边形
与四边形 、抛物线
、抛物线 都有交点时,存在直线
都有交点时,存在直线 ,对于同一条直线
,对于同一条直线 上的交点,直线
上的交点,直线 与四边形
与四边形 的交点的纵坐标都不大于它与抛物线
的交点的纵坐标都不大于它与抛物线 的交点的纵坐标.
的交点的纵坐标.
①当 时,直接写出
时,直接写出 的取值范围;
的取值范围;
②求 的取值范围.
的取值范围.
 与
与 轴交于
轴交于 ,
, 两点,与
两点,与 轴交于点
轴交于点 .直线
.直线 由直线
由直线 平移得到,与
平移得到,与 轴交于点
轴交于点 .四边形
.四边形 的四个顶点的坐标分别为
的四个顶点的坐标分别为 ,
, ,
, ,
, .
.
(1)填空:
 ______,
______, ______;
______;(2)若点
 在第二象限,直线
在第二象限,直线 与经过点
与经过点 的双曲线
的双曲线 有且只有一个交点,求
有且只有一个交点,求 的最大值;
的最大值;(3)当直线
 与四边形
与四边形 、抛物线
、抛物线 都有交点时,存在直线
都有交点时,存在直线 ,对于同一条直线
,对于同一条直线 上的交点,直线
上的交点,直线 与四边形
与四边形 的交点的纵坐标都不大于它与抛物线
的交点的纵坐标都不大于它与抛物线 的交点的纵坐标.
的交点的纵坐标.①当
 时,直接写出
时,直接写出 的取值范围;
的取值范围;②求
 的取值范围.
的取值范围.23.中国是世界上首先使用负数的国家.两千多年前战国时期李悝所著的《法经》中已出现使用负数的实例.《九章算术》的“方程”一章,在世界数学史上首次正式引入负数及其加减法运算法则,并给出名为“正负术”的算法.请计算以下涉及“负数”的式子的值: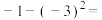
________ .
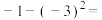
24.求代数式 的值,其中
的值,其中 .
.
 的值,其中
的值,其中 .
. 搜索
搜索
 难度系数:0.85
难度系数:0.85  答案解析
答案解析
 有奖纠错
有奖纠错






