全一卷
1.已知 为第四象限角,则
为第四象限角,则 ,则
,则 ( )
( )
 为第四象限角,则
为第四象限角,则 ,则
,则 ( )
( )A. | B. | C. | D. |
2.已知 ,集合
,集合 ,
, ,
, ,则
,则 ( )
( )
 ,集合
,集合 ,
, ,
, ,则
,则 ( )
( )A.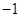 | B. | C. | D.1 |
3.已知抛物线 的焦点为
的焦点为 ,点
,点 在抛物线上且横坐标为4,则
在抛物线上且横坐标为4,则 ( )
( )
 的焦点为
的焦点为 ,点
,点 在抛物线上且横坐标为4,则
在抛物线上且横坐标为4,则 ( )
( )| A.2 | B.3 | C.5 | D.6 |
4.十项全能是由跑、跳、投等10个田径项目组成的综合性男子比赛项目,按照国际田径联合会制定的田径运动全能评分表计分,然后将各个单项的得分相加,总分多者为优胜.下面是某次全能比赛中甲、乙两名运动员的各个单项得分的雷达图.

下列说法错误的是( )

下列说法错误的是( )
| A.在100米项目中,甲的得分比乙高 |
| B.在跳高和标枪项目中,甲、乙的得分基本相同 |
| C.甲的各项得分比乙更均衡 |
| D.甲的总分高于乙的总分 |
5.已知函数 ,若
,若 ,则实数
,则实数 的取值范围是( )
的取值范围是( )
 ,若
,若 ,则实数
,则实数 的取值范围是( )
的取值范围是( )A. | B. |
C. | D. |
6.任何一个复数 (其中
(其中 ,
, 为虚数单位)都可以表示成
为虚数单位)都可以表示成 (其中
(其中 ,
, )的形式,通常称之为复数
)的形式,通常称之为复数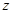 的三角形式.法国数学家棣莫弗发现:
的三角形式.法国数学家棣莫弗发现: ,我们称这个结论为棣莫弗定理.由棣莫弗定理可知,“
,我们称这个结论为棣莫弗定理.由棣莫弗定理可知,“ 为偶数”是“复数
为偶数”是“复数 为纯虚数的是( )
为纯虚数的是( )
 (其中
(其中 ,
, 为虚数单位)都可以表示成
为虚数单位)都可以表示成 (其中
(其中 ,
, )的形式,通常称之为复数
)的形式,通常称之为复数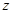 的三角形式.法国数学家棣莫弗发现:
的三角形式.法国数学家棣莫弗发现: ,我们称这个结论为棣莫弗定理.由棣莫弗定理可知,“
,我们称这个结论为棣莫弗定理.由棣莫弗定理可知,“ 为偶数”是“复数
为偶数”是“复数 为纯虚数的是( )
为纯虚数的是( )| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
7.已知点 ,
, ,
, 均在半径为
均在半径为 的圆上,若
的圆上,若 ,则
,则 的最大值为( )
的最大值为( )
 ,
, ,
, 均在半径为
均在半径为 的圆上,若
的圆上,若 ,则
,则 的最大值为( )
的最大值为( )A. | B. | C.4 | D. |
8.在三棱锥 中,
中,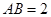 ,
, ,若该三棱锥的体积为
,若该三棱锥的体积为 ,则其外接球表面积的最小值为( )
,则其外接球表面积的最小值为( )
 中,
中,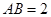 ,
, ,若该三棱锥的体积为
,若该三棱锥的体积为 ,则其外接球表面积的最小值为( )
,则其外接球表面积的最小值为( )A. | B. | C. | D. |
9.已知在某市的一次学情检测中,学生的数学成绩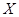 服从正态分布
服从正态分布 ,其中90分为及格线,120分为优秀线.下列说法正确的是( ).
,其中90分为及格线,120分为优秀线.下列说法正确的是( ).
附:随机变量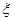 服从正态分布
服从正态分布 ,则
,则 ,
, ,
,
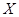 服从正态分布
服从正态分布 ,其中90分为及格线,120分为优秀线.下列说法正确的是( ).
,其中90分为及格线,120分为优秀线.下列说法正确的是( ).附:随机变量
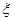 服从正态分布
服从正态分布 ,则
,则 ,
, ,
,
| A.该市学生数学成绩的期望为100 |
| B.该市学生数学成绩的标准差为100 |
| C.该市学生数学成绩及格率超过0.8 |
| D.该市学生数学成绩不及格的人数和优秀的人数大致相等 |
10.已知圆锥的顶点为 ,母线长为2,底面半径为
,母线长为2,底面半径为 ,
, ,
, 为底面圆周上两个动点,则下列说法正确的是( )
为底面圆周上两个动点,则下列说法正确的是( )
 ,母线长为2,底面半径为
,母线长为2,底面半径为 ,
, ,
, 为底面圆周上两个动点,则下列说法正确的是( )
为底面圆周上两个动点,则下列说法正确的是( )| A.圆锥的高为1 |
B.三角形 为等腰三角形 为等腰三角形 |
C.三角形 面积的最大值为 面积的最大值为 |
D.直线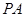 与圆锥底面所成角的大小为 与圆锥底面所成角的大小为 |
11.已知实数 ,
, ,
,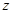 满足
满足 ,则下列关系式中可能成立的是( )
,则下列关系式中可能成立的是( )
 ,
, ,
,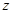 满足
满足 ,则下列关系式中可能成立的是( )
,则下列关系式中可能成立的是( )A. | B. | C. | D. |
12.已知函数 (其中,
(其中, ,
, ),
), ,
, 恒成立,且
恒成立,且 在区间
在区间 上单调,则下列说法正确的是( )
上单调,则下列说法正确的是( )
 (其中,
(其中, ,
, ),
), ,
, 恒成立,且
恒成立,且 在区间
在区间 上单调,则下列说法正确的是( )
上单调,则下列说法正确的是( )A.存在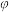 ,使得 ,使得 是偶函数 是偶函数 | B. |
C. 是奇数 是奇数 | D. 的最大值为3 的最大值为3 |
13.5G指的是第五代移动通信技术,比第四代移动通信技术的数据传输速率快数百倍,某公司在研发5G项目时遇到一项技术难题,由甲、乙两个部门分别独立攻关,已知甲部门攻克该技术难题的概率为0.6,乙部门攻克该技术难题的概率为0.5.则该公司攻克这项技术难题的概率为________ .
14.能够说明“若 ,则
,则 ”是假命题的一组整数
”是假命题的一组整数 ,
, 的值依次为
的值依次为________ .
 ,则
,则 ”是假命题的一组整数
”是假命题的一组整数 ,
, 的值依次为
的值依次为15.已知函数 ,若
,若 有两个零点,则实数
有两个零点,则实数 的取值范围是________.
的取值范围是________.
 ,若
,若 有两个零点,则实数
有两个零点,则实数 的取值范围是________.
的取值范围是________.16.已知 ,
, 分别是双曲线
分别是双曲线 的左,右焦点,过点
的左,右焦点,过点 向一条渐近线作垂线,交双曲线右支于点
向一条渐近线作垂线,交双曲线右支于点 ,直线
,直线 与
与 轴交于点
轴交于点 (
( ,
, 在
在 轴同侧),连接
轴同侧),连接 ,若
,若 的内切圆圆心恰好落在以
的内切圆圆心恰好落在以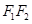 为直径的圆上,则
为直径的圆上,则 的大小为________;双曲线的离心率为________.
的大小为________;双曲线的离心率为________.
 ,
, 分别是双曲线
分别是双曲线 的左,右焦点,过点
的左,右焦点,过点 向一条渐近线作垂线,交双曲线右支于点
向一条渐近线作垂线,交双曲线右支于点 ,直线
,直线 与
与 轴交于点
轴交于点 (
( ,
, 在
在 轴同侧),连接
轴同侧),连接 ,若
,若 的内切圆圆心恰好落在以
的内切圆圆心恰好落在以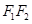 为直径的圆上,则
为直径的圆上,则 的大小为________;双曲线的离心率为________.
的大小为________;双曲线的离心率为________.17.2020年4月21日,习近平总书记到安康市平利县老县镇考察调研,在镇中心小学的课堂上向孩子们发出了“文明其精神,野蛮其体魄”的期许某市教育部门为了了解全市01中学生疫情期间居家体育锻炼的情况,从全市随机抽1000名中学生进行调查,统计他们每周参加体育锻炼的时长,右图是根据调查结果绘制的频率分布直方图.

(1)已知样本中每周体育锻炼时长不足4小时的体育锻炼的中学生有100人,求直方图中 ,
, 的值;
的值;
(2)为了更具体地了解全市中学生疫情期间的体育锻炼情况,利用分层抽样的方法从 和
和 两组中共抽取了6名中学生参加线上座谈会,现从上述6名学生中随机抽取2名在会上进行体育锻炼视频展示,求这2名学生来自不同组的概率.
两组中共抽取了6名中学生参加线上座谈会,现从上述6名学生中随机抽取2名在会上进行体育锻炼视频展示,求这2名学生来自不同组的概率.

(1)已知样本中每周体育锻炼时长不足4小时的体育锻炼的中学生有100人,求直方图中
 ,
, 的值;
的值;(2)为了更具体地了解全市中学生疫情期间的体育锻炼情况,利用分层抽样的方法从
 和
和 两组中共抽取了6名中学生参加线上座谈会,现从上述6名学生中随机抽取2名在会上进行体育锻炼视频展示,求这2名学生来自不同组的概率.
两组中共抽取了6名中学生参加线上座谈会,现从上述6名学生中随机抽取2名在会上进行体育锻炼视频展示,求这2名学生来自不同组的概率.18.已知 中,三个内角
中,三个内角 ,
, ,
, 所对的边分别是
所对的边分别是 ,
, ,
, .
.
(1)证明: ;
;
(2)在① ,②
,② ,③
,③ 这三个条件中任选一个补充在下面问题中,并解答
这三个条件中任选一个补充在下面问题中,并解答
若 ,
, ,________,求
,________,求 的周长.
的周长.
 中,三个内角
中,三个内角 ,
, ,
, 所对的边分别是
所对的边分别是 ,
, ,
, .
.(1)证明:
 ;
;(2)在①
 ,②
,② ,③
,③ 这三个条件中任选一个补充在下面问题中,并解答
这三个条件中任选一个补充在下面问题中,并解答若
 ,
, ,________,求
,________,求 的周长.
的周长.19.如图,三棱维 中,平面
中,平面 平面
平面 ,
, ,
, ,
, 是棱
是棱 的中点,点
的中点,点 在棱
在棱 上点
上点 是
是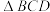 的重心.
的重心.

(1)若 是
是 的中点,证明
的中点,证明 面
面 ;
;
(2)是否存在点 ,使二面角
,使二面角 的大小为
的大小为 ,若存在,求
,若存在,求 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
 中,平面
中,平面 平面
平面 ,
, ,
, ,
, 是棱
是棱 的中点,点
的中点,点 在棱
在棱 上点
上点 是
是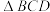 的重心.
的重心.
(1)若
 是
是 的中点,证明
的中点,证明 面
面 ;
;(2)是否存在点
 ,使二面角
,使二面角 的大小为
的大小为 ,若存在,求
,若存在,求 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.20.如图1,杨辉三角是我国南宋数学家杨辉于1261年所著的《详解九章算法》中列出的一张图表,如图2,把杨辉三角左对齐排列,将同一条斜线上的数字求和,会得到一个数列 ,其中
,其中 ,
,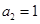 ,
, …设数列
…设数列 的前
的前 项和为
项和为 .
.


(1)求 的值,并写
的值,并写 ,
, ,
, 出满足的递推关系式(不用证明);
出满足的递推关系式(不用证明);
(2)记 ,用
,用 表示
表示 .
.
 ,其中
,其中 ,
,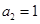 ,
, …设数列
…设数列 的前
的前 项和为
项和为 .
.

(1)求
 的值,并写
的值,并写 ,
, ,
, 出满足的递推关系式(不用证明);
出满足的递推关系式(不用证明);(2)记
 ,用
,用 表示
表示 .
.21.已知椭圆 的左顶点和下顶点分别为
的左顶点和下顶点分别为 ,
, ,
, ,过椭圆焦点且与长轴垂直的弦的长为2.
,过椭圆焦点且与长轴垂直的弦的长为2.
(1)求椭圆 的方程;
的方程;
(2)已知 为椭圆
为椭圆 上一动点(
上一动点( 不与
不与 ,
, 重合),直线
重合),直线 与
与 轴交于点
轴交于点 ,直线
,直线 与
与 轴交于点
轴交于点 ,证明:
,证明: 为定值.
为定值.
 的左顶点和下顶点分别为
的左顶点和下顶点分别为 ,
, ,
, ,过椭圆焦点且与长轴垂直的弦的长为2.
,过椭圆焦点且与长轴垂直的弦的长为2.(1)求椭圆
 的方程;
的方程;(2)已知
 为椭圆
为椭圆 上一动点(
上一动点( 不与
不与 ,
, 重合),直线
重合),直线 与
与 轴交于点
轴交于点 ,直线
,直线 与
与 轴交于点
轴交于点 ,证明:
,证明: 为定值.
为定值.22.已知函数 存在唯一的极值点
存在唯一的极值点 .
.
(1)求实数 的取值范围;
的取值范围;
(2)若 ,证明:
,证明: .
.
 存在唯一的极值点
存在唯一的极值点 .
.(1)求实数
 的取值范围;
的取值范围;(2)若
 ,证明:
,证明: .
. 搜索
搜索
 难度系数:0.85
难度系数:0.85  答案解析
答案解析
 有奖纠错
有奖纠错
