全一卷
1.已知复数 ,其中
,其中 为虚数单位,则复数
为虚数单位,则复数 ( )
( )
 ,其中
,其中 为虚数单位,则复数
为虚数单位,则复数 ( )
( )A. | B. | C. | D. |
2.设集合 ,
, ,则
,则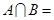 ( )
( )
 ,
, ,则
,则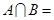 ( )
( )A. | B. | C. | D. |
3.要得到函数 的图象,只需将函数
的图象,只需将函数 的图象( )
的图象( )
 的图象,只需将函数
的图象,只需将函数 的图象( )
的图象( )A.向左平移 个单位 个单位 | B.向右平移 个单位 个单位 | C.向上平移 个单位 个单位 | D.向下平移 个单位 个单位 |
4.已知直线 与直线
与直线 平行,则实数
平行,则实数 ( )
( )
| A. | B.3 | C.5 | D. |
5.将编号为001,002,003,…,300的300个产品,按编号从小到大的顺序均匀的分成若干组,采用每小组选取的号码间隔一样的系统抽样方法抽取一个样本,若第一组抽取的编号是003,第二组抽取的编号是018,则样本中最大的编号应该是( )
| A.283 | B.286 | C.287 | D.288 |
6.设 ,则
,则 ,
, ,
, 的大小关系为( )
的大小关系为( )
 ,则
,则 ,
, ,
, 的大小关系为( )
的大小关系为( )A. | B. | C. | D. |
7.在平面直角坐标系 中,已知角
中,已知角 的顶点在坐标原点,始边与
的顶点在坐标原点,始边与 轴正半轴重合,终边经过点
轴正半轴重合,终边经过点 ,则
,则 ( )
( )
 中,已知角
中,已知角 的顶点在坐标原点,始边与
的顶点在坐标原点,始边与 轴正半轴重合,终边经过点
轴正半轴重合,终边经过点 ,则
,则 ( )
( )A. | B. | C. | D. |
8.已知△ 的三边分别为
的三边分别为 ,
, ,
, ,且满足
,且满足 ,则△
,则△ 的最大内角为( )
的最大内角为( )
 的三边分别为
的三边分别为 ,
, ,
, ,且满足
,且满足 ,则△
,则△ 的最大内角为( )
的最大内角为( )A. | B.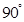 | C. | D. |
9.如图,网格纸上小正方形的边长为1,粗线画出的是一个三棱锥的三视图,则该三棱锥外接球的体积是( )


A. | B. | C. | D. |
10.已知正方形 的边长为1,点
的边长为1,点 满足
满足 ,设
,设 与
与 交于点
交于点 ,则
,则 ( )
( )
 的边长为1,点
的边长为1,点 满足
满足 ,设
,设 与
与 交于点
交于点 ,则
,则 ( )
( )| A.1 | B.2 | C.3 | D.4 |
11.在生活中,我们常看到各种各样的简易遮阳棚.现有直径为 的圆面,在圆周上选定一个点固定在水平的地面上,然后将圆面撑起,使得圆面与南北方向的某一直线平行,做成简易遮阳棚.设正东方向射出的太阳光线与地面成
的圆面,在圆周上选定一个点固定在水平的地面上,然后将圆面撑起,使得圆面与南北方向的某一直线平行,做成简易遮阳棚.设正东方向射出的太阳光线与地面成 角,若要使所遮阴影面的面积最大,那么圆面与阴影面所成角的大小为( )
角,若要使所遮阴影面的面积最大,那么圆面与阴影面所成角的大小为( )
 的圆面,在圆周上选定一个点固定在水平的地面上,然后将圆面撑起,使得圆面与南北方向的某一直线平行,做成简易遮阳棚.设正东方向射出的太阳光线与地面成
的圆面,在圆周上选定一个点固定在水平的地面上,然后将圆面撑起,使得圆面与南北方向的某一直线平行,做成简易遮阳棚.设正东方向射出的太阳光线与地面成 角,若要使所遮阴影面的面积最大,那么圆面与阴影面所成角的大小为( )
角,若要使所遮阴影面的面积最大,那么圆面与阴影面所成角的大小为( )A. | B. | C. | D. |
12.已知 ,
, 分别是双曲线
分别是双曲线 的左、右焦点,点
的左、右焦点,点 为双曲线右支上的点.若
为双曲线右支上的点.若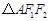 的内切圆与
的内切圆与 轴切于点
轴切于点 ,且
,且 ,则该双曲线的离心率为( )
,则该双曲线的离心率为( )
 ,
, 分别是双曲线
分别是双曲线 的左、右焦点,点
的左、右焦点,点 为双曲线右支上的点.若
为双曲线右支上的点.若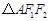 的内切圆与
的内切圆与 轴切于点
轴切于点 ,且
,且 ,则该双曲线的离心率为( )
,则该双曲线的离心率为( )A. | B. | C.2 | D. |
13.设曲线 在
在 处的切线方程为
处的切线方程为 ,则实数
,则实数 的值为
的值为________ .
 在
在 处的切线方程为
处的切线方程为 ,则实数
,则实数 的值为
的值为14.已知 ,
, ,
, ,则
,则 的最小值为________.
的最小值为________.
 ,
, ,
, ,则
,则 的最小值为________.
的最小值为________.15.已知α、β为锐角, ,
, .则
.则
________ .
 ,
, .则
.则
16.已知 是定义域为
是定义域为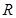 的偶函数,对
的偶函数,对 ,有
,有 ,且当
,且当 时,
时, ,函数
,函数 .现给出以下命题:①
.现给出以下命题:① 是周期函数;②
是周期函数;② 的图象关于直线
的图象关于直线 对称;③当
对称;③当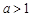 时,
时,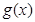 在
在 内有一个零点;④当
内有一个零点;④当 时,
时,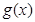 在
在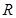 上至少有六个零.其中正确命题的序号为________.
上至少有六个零.其中正确命题的序号为________.
 是定义域为
是定义域为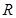 的偶函数,对
的偶函数,对 ,有
,有 ,且当
,且当 时,
时, ,函数
,函数 .现给出以下命题:①
.现给出以下命题:① 是周期函数;②
是周期函数;② 的图象关于直线
的图象关于直线 对称;③当
对称;③当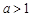 时,
时,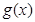 在
在 内有一个零点;④当
内有一个零点;④当 时,
时,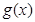 在
在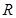 上至少有六个零.其中正确命题的序号为________.
上至少有六个零.其中正确命题的序号为________.17.已知公差不为0的等差数列 ,其前
,其前 项和为
项和为 ,
, ,且
,且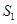 、
、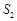 、
、 成等比数列.
成等比数列.
(1)求数列 的通项公式;
的通项公式;
(2)令 ,求数列
,求数列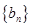 的前
的前 项和
项和 .
.
 ,其前
,其前 项和为
项和为 ,
, ,且
,且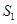 、
、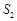 、
、 成等比数列.
成等比数列.(1)求数列
 的通项公式;
的通项公式;(2)令
 ,求数列
,求数列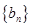 的前
的前 项和
项和 .
.18.在四棱锥 中,
中, 平面
平面 ,底面
,底面 为梯形,
为梯形, ,
, ,
, ,
, ,
, ,点
,点 ,
, 分别为线段
分别为线段 ,
, 的中点.
的中点.

(1)证明: 平面
平面 ;
;
(2)求点 到平面
到平面 的距离.
的距离.
 中,
中, 平面
平面 ,底面
,底面 为梯形,
为梯形, ,
, ,
, ,
, ,
, ,点
,点 ,
, 分别为线段
分别为线段 ,
, 的中点.
的中点.
(1)证明:
 平面
平面 ;
;(2)求点
 到平面
到平面 的距离.
的距离.19.已知抛物线 的焦点
的焦点 到直线
到直线 的距离为
的距离为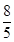 .
.
(1)求抛物线 的方程;
的方程;
(2)直线 与抛物线
与抛物线 交于
交于 ,
, 两点,
两点, 为坐标原点,设直线
为坐标原点,设直线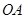 的斜率为
的斜率为 ,直线
,直线 的斜率为
的斜率为 ,求
,求 的值.
的值.
 的焦点
的焦点 到直线
到直线 的距离为
的距离为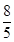 .
.(1)求抛物线
 的方程;
的方程;(2)直线
 与抛物线
与抛物线 交于
交于 ,
, 两点,
两点, 为坐标原点,设直线
为坐标原点,设直线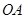 的斜率为
的斜率为 ,直线
,直线 的斜率为
的斜率为 ,求
,求 的值.
的值.20.近几年,电商行业的蓬勃发展带动了快递业的迅速增长,快递公司揽收价格一般是采用“首重+续重”的计价方式.首重是指最低的计费重量,续重是指超过首重部分的计费重量,不满一公斤按一公斤计费.某快递网点将快件的揽收价格定为首重(不超过一公斤)8元,续重2元/公斤(例如,若一个快件的重量是0.6公斤,按8元计费;若一个快件的重量是1.4公斤,按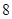 元
元 元
元 元计费).根据历史数据,得到该网点揽收快件重量的频率分布直方图如下图所示
元计费).根据历史数据,得到该网点揽收快件重量的频率分布直方图如下图所示

(1)根据样本估计总体的思想,将频率视作概率,求该网点揽收快件的平均价格;
(2)为了获得更大的利润,该网点对“一天中收发一件快递的平均成本 (单位:元)与当天揽收的快递件数
(单位:元)与当天揽收的快递件数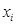 (单位:百件)
(单位:百件) 之间的关系”进行调查研究,得到相关数据如下表:
之间的关系”进行调查研究,得到相关数据如下表:
根据以上数据,技术人员分别根据甲、乙两种不同的回归模型,得到两个回归方程:
方程甲: ,方程乙:
,方程乙: .
.
①为了评价两种模型的拟合效果,根据上表数据和相应回归方程,将以下表格填写完整(结果保留一位小数),分别计算模型甲与模型乙的残差平方和 ,
, ,并依此判断哪个模型的拟合效果更好(备注:
,并依此判断哪个模型的拟合效果更好(备注: 称为相应于点
称为相应于点 的残差,残差平方和
的残差,残差平方和 ;
;
②预计该网点今年6月25日(端午节)一天可以揽收1000件快递,试根据①中确定的拟合效果较好的回归模型估计该网点当天的总利润(总利润=(平均价格-平均成本)×总件数).
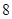 元
元 元
元 元计费).根据历史数据,得到该网点揽收快件重量的频率分布直方图如下图所示
元计费).根据历史数据,得到该网点揽收快件重量的频率分布直方图如下图所示
(1)根据样本估计总体的思想,将频率视作概率,求该网点揽收快件的平均价格;
(2)为了获得更大的利润,该网点对“一天中收发一件快递的平均成本
 (单位:元)与当天揽收的快递件数
(单位:元)与当天揽收的快递件数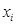 (单位:百件)
(单位:百件) 之间的关系”进行调查研究,得到相关数据如下表:
之间的关系”进行调查研究,得到相关数据如下表:每天揽收快递件数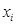 (百件) (百件) | 2 | 3 | 4 | 5 | 8 |
每件快递的平均成本 (元) (元) | 5.6 | 4.8 | 4.4 | 4.3 | 4.1 |
根据以上数据,技术人员分别根据甲、乙两种不同的回归模型,得到两个回归方程:
方程甲:
 ,方程乙:
,方程乙: .
.①为了评价两种模型的拟合效果,根据上表数据和相应回归方程,将以下表格填写完整(结果保留一位小数),分别计算模型甲与模型乙的残差平方和
 ,
, ,并依此判断哪个模型的拟合效果更好(备注:
,并依此判断哪个模型的拟合效果更好(备注: 称为相应于点
称为相应于点 的残差,残差平方和
的残差,残差平方和 ;
;每天揽收快递件数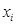 /百件 /百件 | 2 | 3 | 4 | 5 | 8 | |
每天快递的平均成本 /元 /元 | 5.6 | 4.8 | 4.4 | 4.3 | 4.1 | |
| 模型甲 | 预报值 | 5.2 | 5.0 | 4.8 | | |
残差 |  | 0.2 | 0.4 | | | |
| 模型乙 | 预报值 | 5.5 | 4.8 | 4.5 | | |
预报值 |  | 0 | 0.1 | | | |
②预计该网点今年6月25日(端午节)一天可以揽收1000件快递,试根据①中确定的拟合效果较好的回归模型估计该网点当天的总利润(总利润=(平均价格-平均成本)×总件数).
21.已知函数 .
.
(1)讨论函数 的单调性;
的单调性;
(2)证明:当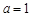 时,
时, .
.
 .
.(1)讨论函数
 的单调性;
的单调性;(2)证明:当
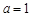 时,
时, .
.22.在直角坐标系 中,以
中,以 为极点,
为极点, 轴正半轴为极轴建立极坐标系.已知曲线
轴正半轴为极轴建立极坐标系.已知曲线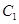 的参数方程为
的参数方程为 (
( 为参数,
为参数, ),曲线
),曲线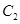 的极坐标方程为
的极坐标方程为 ,点
,点 是
是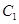 与
与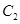 的一个交点,其极坐标为
的一个交点,其极坐标为 .设射线
.设射线 与曲线
与曲线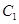 相交于
相交于 ,
, 两点,与曲线
两点,与曲线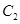 相交于
相交于 ,
, 两点.
两点.
(1)求 ,
, 的值;
的值;
(2)求 的最大值.
的最大值.
 中,以
中,以 为极点,
为极点, 轴正半轴为极轴建立极坐标系.已知曲线
轴正半轴为极轴建立极坐标系.已知曲线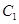 的参数方程为
的参数方程为 (
( 为参数,
为参数, ),曲线
),曲线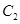 的极坐标方程为
的极坐标方程为 ,点
,点 是
是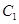 与
与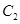 的一个交点,其极坐标为
的一个交点,其极坐标为 .设射线
.设射线 与曲线
与曲线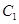 相交于
相交于 ,
, 两点,与曲线
两点,与曲线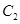 相交于
相交于 ,
, 两点.
两点.(1)求
 ,
, 的值;
的值;(2)求
 的最大值.
的最大值.23.设函数 ,集合
,集合 为不等式
为不等式 的解集.
的解集.
(1)求集合 ;
;
(2)当 ,
, 时,证明:
时,证明: .
.
 ,集合
,集合 为不等式
为不等式 的解集.
的解集.(1)求集合
 ;
;(2)当
 ,
, 时,证明:
时,证明: .
. 搜索
搜索
 难度系数:0.94
难度系数:0.94  答案解析
答案解析
 有奖纠错
有奖纠错
