搜索
全一卷
难度系数：0.65 
答案解析
有奖纠错
1．已知△ABC的外接圆半径为R,且 
,其中,a、b分别为∠A、∠B的对边则∠C的大小为______.
,其中,a、b分别为∠A、∠B的对边则∠C的大小为______.2．设集合
, 
,
则a的取值范围是______.
, 
,
则a的取值范围是______.3．
被8除所得的余数为______.
被8除所得的余数为______.4．在数列
中, 
, 
,对所有的正整数n均有
则
______.
中, 
, 
,对所有的正整数n均有
则
______.5．如图,在底面为直角梯形的四棱锥
中,
,
,PA⊥平面ABCD,PA=3,AD=2, 
,BC=6.则二面角
的大小为______.
中,
,
,PA⊥平面ABCD,PA=3,AD=2, 
,BC=6.则二面角
的大小为______.
6．设双曲线
的左、右焦点分别为F1、F2,A为双曲线渐近线上的一点,
,原点O到直线AF1的距离为
.则双曲线的离心率为______.
的左、右焦点分别为F1、F2,A为双曲线渐近线上的一点,
,原点O到直线AF1的距离为
.则双曲线的离心率为______.7．已知a、b为两个互相垂直的单位向量,且
.则对任意的正实数t, 
的最小值为______.
.则对任意的正实数t, 
的最小值为______.8．若关于
的方程
有四个不同的实数解,则实数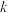
的取值范围是___________
的方程
有四个不同的实数解,则实数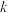
的取值范围是9．设
、
为正实数,且x+y=1.则
的最小值为______.
、
为正实数,且x+y=1.则
的最小值为______.10．设f(x)为定义在整数集上的函数,满足条件
(1)
,
;
(2)对任意的
、
均有
则
______.
(1)
,
;(2)对任意的
、
均有
则
______.11．已知函数 
(1)求
的最小正周期和单调递减区间;
(2)若
在
上恒成立,求实数
的取值范围.
(1)求
的最小正周期和单调递减区间;(2)若
在上恒成立,求实数的取值范围.12．某花店每天以每枝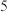
元的价格从农场购进若干枝玫瑰花，然后以每枝
元的价格出售，如果当天卖不完，剩下的玫瑰花作垃圾处理.
（1）若花店一天购进
枝玫瑰花，求当天的利润
(单位：元)关于当天需求量
（单位：枝，
）的函数解析式.
（2）花店记录了100天玫瑰花的日需求量（单位：枝），整理得下表：
以100天记录的各需求量的频率作为各需求量发生的概率.
（i）若花店一天购进枝玫瑰花，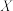
表示当天的利润（单位：元），求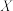的分布列，数学期望及方差；
（ii）若花店计划一天购进16枝或17枝玫瑰花，你认为应购进16枝还是17枝？请说明理由.
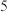元的价格从农场购进若干枝玫瑰花，然后以每枝
元的价格出售，如果当天卖不完，剩下的玫瑰花作垃圾处理.（1）若花店一天购进
枝玫瑰花，求当天的利润
(单位：元)关于当天需求量
（单位：枝，
）的函数解析式.（2）花店记录了100天玫瑰花的日需求量（单位：枝），整理得下表：
以100天记录的各需求量的频率作为各需求量发生的概率.
（i）若花店一天购进
枝玫瑰花，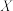
表示当天的利润（单位：元），求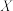的分布列，数学期望及方差；（ii）若花店计划一天购进16枝或17枝玫瑰花，你认为应购进16枝还是17枝？请说明理由.
13．数列满足, 
(1)设
,求数列
的通项公式;
(2)设
,数列
的前n项和为
,求.
满足, 
(1)设
,求数列
的通项公式;(2)设
,数列
的前n项和为
,求.14．已知函数
(1)若函数
在区间
上为单调增函数,求
的取值范围;
(2)设
,证明: 
①
(1)若函数
在区间
上为单调增函数,求
的取值范围;(2)设
,证明: 
①15．已知椭圆
: 
的左、右焦点为F1、F2,设点F1、F2与椭圆短轴的一个端点构成边长为4的正三角形.
(1)求椭圆的标准方程;
(2)过椭圆上任意一点
作椭圆的切线与直线
的垂线
交于点M,求点M的轨迹方程;
(3)若切线
与直线
交于点,证明:
为定值.
: 
的左、右焦点为F1、F2,设点F1、F2与椭圆短轴的一个端点构成边长为4的正三角形.(1)求椭圆
的标准方程;(2)过椭圆
上任意一点
作椭圆的切线与直线
的垂线
交于点M,求点M的轨迹方程;(3)若切线
与直线
交于点,证明:
为定值.