全一卷
1.给定公比为 的等比数列
的等比数列 ,设
,设 ,
, ,则数列
,则数列 ( ).
( ).
 的等比数列
的等比数列 ,设
,设 ,
, ,则数列
,则数列 ( ).
( ).| A.是等差数列 | B.是公比为 的等比数列 的等比数列 |
C.是公比为 的等比数列 的等比数列 | D.既非等差数列又非等比数列 |
2.平面直角坐标系中,纵、横坐标都是整数的点叫做整点.那么,满足不等式 的整点
的整点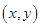 的个数是( ).
的个数是( ).
 的整点
的整点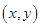 的个数是( ).
的个数是( ).| A.16 | B.17 | C.18 | D.25 |
3.若 ,则( ).
,则( ).
 ,则( ).
,则( ).A. | B. | C. | D. |
4.给定下列两个关于异面直线的命题:命题Ⅰ :若平面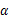 上的直线
上的直线 与平面
与平面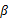 上的直线
上的直线 为异面直线,直线
为异面直线,直线 是
是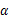 与
与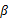 的交线,那么,
的交线,那么, 至多与
至多与 、
、 中的一条相交;命题Ⅱ :不存在这样的无穷多条直线,它们中的任意两条都是异面直线.
中的一条相交;命题Ⅱ :不存在这样的无穷多条直线,它们中的任意两条都是异面直线.
那么,( ).
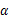 上的直线
上的直线 与平面
与平面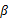 上的直线
上的直线 为异面直线,直线
为异面直线,直线 是
是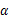 与
与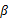 的交线,那么,
的交线,那么, 至多与
至多与 、
、 中的一条相交;命题Ⅱ :不存在这样的无穷多条直线,它们中的任意两条都是异面直线.
中的一条相交;命题Ⅱ :不存在这样的无穷多条直线,它们中的任意两条都是异面直线.那么,( ).
| A.命题Ⅰ 正确,命题Ⅱ 不正确 | B.命题Ⅱ 正确,命题Ⅰ 不正确 |
| C.两个命题都正确 | D.两个命题都不正确 |
5.在某次乒乓球单打比赛中,原计划每两名选手各比赛一场,但有三名选手各比赛两场之后就退出了,这样全部比赛只进行了50场. 则上述三名选手之间比赛的场数为( )
| A.0 | B.1 | C.2 | D.3 |
6.已知点 ,过点
,过点 的直线与抛物线
的直线与抛物线 交于另外两点
交于另外两点 、
、 .那么,
.那么, 是( ).
是( ).
 ,过点
,过点 的直线与抛物线
的直线与抛物线 交于另外两点
交于另外两点 、
、 .那么,
.那么, 是( ).
是( ).| A.锐角三角形 | B.钝角三角形 | C.直角三角形 | D.答案不确定 |
7.已知正整数 不超过2000,并且能表示成不少于60个连续正整数之和.那么,这样的
不超过2000,并且能表示成不少于60个连续正整数之和.那么,这样的 的个数是______.
的个数是______.
 不超过2000,并且能表示成不少于60个连续正整数之和.那么,这样的
不超过2000,并且能表示成不少于60个连续正整数之和.那么,这样的 的个数是______.
的个数是______.8.已知 .那么,复数
.那么,复数 的辐角主值是______.
的辐角主值是______.
 .那么,复数
.那么,复数 的辐角主值是______.
的辐角主值是______.9.在 中,记
中,记 ,
, ,
, .若
.若 ,则
,则
______ .
 中,记
中,记 ,
, ,
, .若
.若 ,则
,则
10.已知点 在双曲线
在双曲线 上,并且
上,并且 到这条这条双曲线的右准线的距离恰是
到这条这条双曲线的右准线的距离恰是 到这条双曲线的两个焦点的距离的等差中项.那么,
到这条双曲线的两个焦点的距离的等差中项.那么, 的横坐标是______.
的横坐标是______.
 在双曲线
在双曲线 上,并且
上,并且 到这条这条双曲线的右准线的距离恰是
到这条这条双曲线的右准线的距离恰是 到这条双曲线的两个焦点的距离的等差中项.那么,
到这条双曲线的两个焦点的距离的等差中项.那么, 的横坐标是______.
的横坐标是______.11.已知直线 中的
中的 、
、 、
、 是取自集合
是取自集合 中的3个不同的元素,并且该直线的倾斜角为锐角.那么,这样的直线的条数是
中的3个不同的元素,并且该直线的倾斜角为锐角.那么,这样的直线的条数是______ .
 中的
中的 、
、 、
、 是取自集合
是取自集合 中的3个不同的元素,并且该直线的倾斜角为锐角.那么,这样的直线的条数是
中的3个不同的元素,并且该直线的倾斜角为锐角.那么,这样的直线的条数是12.已知三棱锥 的底面是正三角形,
的底面是正三角形, 点在侧面
点在侧面 上的射影
上的射影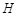 是
是 的垂心,二面角
的垂心,二面角 的平面角等于
的平面角等于 ,
, .那么,三棱锥
.那么,三棱锥 的体积为
的体积为______ .
 的底面是正三角形,
的底面是正三角形, 点在侧面
点在侧面 上的射影
上的射影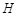 是
是 的垂心,二面角
的垂心,二面角 的平面角等于
的平面角等于 ,
, .那么,三棱锥
.那么,三棱锥 的体积为
的体积为13.已知当 时,不等式
时,不等式 恒成立.试求
恒成立.试求 的取值范围.
的取值范围.
 时,不等式
时,不等式 恒成立.试求
恒成立.试求 的取值范围.
的取值范围.14.给定 ,已知
,已知 是椭圆
是椭圆 上的动点,
上的动点, 是左焦点.当
是左焦点.当 取最小值时,求
取最小值时,求 的坐标.
的坐标.
 ,已知
,已知 是椭圆
是椭圆 上的动点,
上的动点, 是左焦点.当
是左焦点.当 取最小值时,求
取最小值时,求 的坐标.
的坐标.15.给定正整数 和正数
和正数 .对于满足条件
.对于满足条件 的所有等差数列
的所有等差数列 .试求
.试求 的最大值.
的最大值.
 和正数
和正数 .对于满足条件
.对于满足条件 的所有等差数列
的所有等差数列 .试求
.试求 的最大值.
的最大值.16.如图,在四边形 中,对角线
中,对角线 平分
平分 .在
.在 上取一点
上取一点 ,
,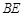 与
与 相交于
相交于 ,延长
,延长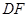 交
交 于
于 .求证:
.求证: .
.

 中,对角线
中,对角线 平分
平分 .在
.在 上取一点
上取一点 ,
,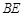 与
与 相交于
相交于 ,延长
,延长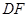 交
交 于
于 .求证:
.求证: .
.
17.给定实数 、
、 、
、 .已知复数
.已知复数 、
、 、
、 满足:
满足: 求
求 的值.
的值.
 、
、 、
、 .已知复数
.已知复数 、
、 、
、 满足:
满足: 求
求 的值.
的值.18.给定正整数 ,已知用克数都是正整数的
,已知用克数都是正整数的 块砝码和一台天平可以称出质量为
块砝码和一台天平可以称出质量为 克的所有物品.
克的所有物品.
(1)求 的最小值
的最小值 ;
;
(2)当且仅当 取什么值时,上述
取什么值时,上述 块砝码的组成方式是惟一确定的?并证明你的结论.
块砝码的组成方式是惟一确定的?并证明你的结论.
 ,已知用克数都是正整数的
,已知用克数都是正整数的 块砝码和一台天平可以称出质量为
块砝码和一台天平可以称出质量为 克的所有物品.
克的所有物品.(1)求
 的最小值
的最小值 ;
;(2)当且仅当
 取什么值时,上述
取什么值时,上述 块砝码的组成方式是惟一确定的?并证明你的结论.
块砝码的组成方式是惟一确定的?并证明你的结论. 搜索
搜索
 难度系数:0.65
难度系数:0.65  答案解析
答案解析
 有奖纠错
有奖纠错
