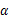 上的直线
上的直线 与平面
与平面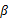 上的直线
上的直线 为异面直线,直线
为异面直线,直线 是
是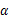 与
与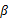 的交线,那么,
的交线,那么, 至多与
至多与 、
、 中的一条相交;命题Ⅱ :不存在这样的无穷多条直线,它们中的任意两条都是异面直线.
中的一条相交;命题Ⅱ :不存在这样的无穷多条直线,它们中的任意两条都是异面直线.那么,( ).
| A.命题Ⅰ 正确,命题Ⅱ 不正确 | B.命题Ⅱ 正确,命题Ⅰ 不正确 |
| C.两个命题都正确 | D.两个命题都不正确 |

同类型试题

y = sin x, x∈R, y∈[–1,1],周期为2π,函数图像以 x = (π/2) + kπ 为对称轴
y = arcsin x, x∈[–1,1], y∈[–π/2,π/2]
sin x = 0 ←→ arcsin x = 0
sin x = 1/2 ←→ arcsin x = π/6
sin x = √2/2 ←→ arcsin x = π/4
sin x = 1 ←→ arcsin x = π/2
y = sin x, x∈R, y∈[–1,1],周期为2π,函数图像以 x = (π/2) + kπ 为对称轴
y = arcsin x, x∈[–1,1], y∈[–π/2,π/2]
sin x = 0 ←→ arcsin x = 0
sin x = 1/2 ←→ arcsin x = π/6
sin x = √2/2 ←→ arcsin x = π/4
sin x = 1 ←→ arcsin x = π/2
 搜索
搜索

