全一卷
1.函数 的反函数
的反函数 .
.
 的反函数
的反函数 .
.2.某算法的程序框图如右图所示,则输出量 与输入量
与输入量 满足的关系式是 .
满足的关系式是 .
 与输入量
与输入量 满足的关系式是 .
满足的关系式是 .
3.若球 、
、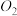 表面积之比
表面积之比 ,则它们的半径之比
,则它们的半径之比
_____ .
 、
、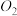 表面积之比
表面积之比 ,则它们的半径之比
,则它们的半径之比
4.已知实数 、
、 满足
满足 ,则目标函数
,则目标函数 的最小值是 .
的最小值是 .
 、
、 满足
满足 ,则目标函数
,则目标函数 的最小值是 .
的最小值是 .5.若等腰直角三角形的直角边长为2,则以一直角边所在的直线为轴旋转一周所成的几何体体积是 .
6.过点 作倾斜角为
作倾斜角为 的直线,与抛物线
的直线,与抛物线 交于
交于 、
、 两点,则
两点,则 的值等于 .
的值等于 .
 作倾斜角为
作倾斜角为 的直线,与抛物线
的直线,与抛物线 交于
交于 、
、 两点,则
两点,则 的值等于 .
的值等于 .7.已知函数 .项数为27的等差数列
.项数为27的等差数列 满足
满足 ,且公差
,且公差 .若
.若 ,则当
,则当 =____________时,
=____________时, .
.
 .项数为27的等差数列
.项数为27的等差数列 满足
满足 ,且公差
,且公差 .若
.若 ,则当
,则当 =____________时,
=____________时, .
.8.已知集合 ,
, ,且
,且 ,
,
则实数a的取值范围是______________________ .
 ,
, ,且
,且 ,
,
则实数a的取值范围是______________________ .

9.若行列式 中,元素4的代数余子式大于0,
中,元素4的代数余子式大于0,
则x满足的条件是________________________ .
 中,元素4的代数余子式大于0,
中,元素4的代数余子式大于0,则x满足的条件是________________________ .
10.如图,若正四棱柱 的底面连长为2,高为4,则异面直线
的底面连长为2,高为4,则异面直线 与AD所成角的大小是______________(结果用反三角函数表示).
与AD所成角的大小是______________(结果用反三角函数表示).
 的底面连长为2,高为4,则异面直线
的底面连长为2,高为4,则异面直线 与AD所成角的大小是______________(结果用反三角函数表示).
与AD所成角的大小是______________(结果用反三角函数表示).
11.函数 的最小值是____________________ .
的最小值是____________________ .
 的最小值是____________________ .
的最小值是____________________ .
12.已知 、
、 是椭圆
是椭圆 (
( >
> >0)的两个焦点,
>0)的两个焦点, 为椭圆
为椭圆 上一点,且
上一点,且 .若
.若 的面积为9,则
的面积为9,则 =____________.
=____________.
 、
、 是椭圆
是椭圆 (
( >
> >0)的两个焦点,
>0)的两个焦点, 为椭圆
为椭圆 上一点,且
上一点,且 .若
.若 的面积为9,则
的面积为9,则 =____________.
=____________.13.若某学校要从5名男生和2名女生中选出3人作为上海世博会的志愿者,则选出的志愿者中男女生均不少于1名的概率是_____________ (结果用最简分数表示).
14.某地街道呈现东——西、南——北向的网络状,相邻街距都为1,两街道相交的点称为格点.若以相互垂直的两条街道为轴建立直角坐标系,现有下述格点(-2,2),(3,1),(3,4),(-2,3),(4,5)为报刊零售店,请确定一个格点 为发行站,使5个零售点沿街道发行站之间路程的和最短.
15.已知直线 :
: 与
与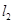 :
: 平行,则
平行,则 的值是( ).
的值是( ).
 :
: 与
与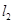 :
: 平行,则
平行,则 的值是( ).
的值是( ).A.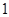 或 或 | B.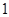 或 或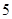 | C. 或 或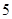 | D.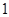 或 或 |
16.如图,已知三棱锥的底面是直角三角形,直角边长分别为3和4,过直角顶点的侧棱长为4,且垂直于底面,该三棱锥的主视图是( )


A. | B. |
C. | D. |
17.在发生某公共卫生事件期间,有专业机构认为该事件在一段时间没有发生在规模群体感染的标志为“连续10天,每天新增疑似病例不超过7人”.根据过去10天甲、乙、丙、丁四地新增疑似病例数据,一定符合该标志的是
| A.甲地:总体均值为3,中位数为4 | B.乙地:总体均值为1,总体方差大于0 |
| C.丙地:中位数为2,众数为3 | D.丁地:总体均值为2,总体方差为3 |
18.点 与圆
与圆 上任一点连线的中点的轨迹方程是
上任一点连线的中点的轨迹方程是
 与圆
与圆 上任一点连线的中点的轨迹方程是
上任一点连线的中点的轨迹方程是A. |
B. |
C. |
D. |
19.已知 的角
的角 、
、 、
、 所对的边分别是
所对的边分别是 、
、 、
、 ,设向量
,设向量 ,
,
 ,
, .
.
(1)若 ,求证:
,求证: 为等腰三角形;
为等腰三角形;
(2)若 ,边长
,边长 ,角
,角 ,求
,求 的面积.
的面积.
 的角
的角 、
、 、
、 所对的边分别是
所对的边分别是 、
、 、
、 ,设向量
,设向量 ,
,
 ,
, .
.(1)若
 ,求证:
,求证: 为等腰三角形;
为等腰三角形;(2)若
 ,边长
,边长 ,角
,角 ,求
,求 的面积.
的面积.20.(本题满分14分)本题共有2个小题,第1小题满分6分,第2小题满分8分.
有时可用函数

描述学习某学科知识的掌握程度,其中x表示某学科知识的学习次数( ),
), 表示对该学科知识的掌握程度,正实数a与学科知识有关.
表示对该学科知识的掌握程度,正实数a与学科知识有关.
(1) 证明:当 时,掌握程度的增加量
时,掌握程度的增加量 总是下降;
总是下降;
(2) 根据经验,学科甲、乙、丙对应的a的取值区间分别为 ,
, ,
,
 .当学习某学科知识6次时,掌握程度是85%,请确定相应的学科.
.当学习某学科知识6次时,掌握程度是85%,请确定相应的学科.
有时可用函数

描述学习某学科知识的掌握程度,其中x表示某学科知识的学习次数(
 ),
), 表示对该学科知识的掌握程度,正实数a与学科知识有关.
表示对该学科知识的掌握程度,正实数a与学科知识有关.(1) 证明:当
 时,掌握程度的增加量
时,掌握程度的增加量 总是下降;
总是下降;(2) 根据经验,学科甲、乙、丙对应的a的取值区间分别为
 ,
, ,
, .当学习某学科知识6次时,掌握程度是85%,请确定相应的学科.
.当学习某学科知识6次时,掌握程度是85%,请确定相应的学科.21.已知 的角
的角 、
、 、
、 所对的边分别是
所对的边分别是 、
、 、
、 ,设向量
,设向量 ,
,
 ,
, .
.
(1)若 ,求证:
,求证: 为等腰三角形;
为等腰三角形;
(2)若 ,边长
,边长 ,角
,角 ,求
,求 的面积.
的面积.
 的角
的角 、
、 、
、 所对的边分别是
所对的边分别是 、
、 、
、 ,设向量
,设向量 ,
,
 ,
, .
.(1)若
 ,求证:
,求证: 为等腰三角形;
为等腰三角形;(2)若
 ,边长
,边长 ,角
,角 ,求
,求 的面积.
的面积.22.
已知双曲线C的中心是原点,右焦点为F ,一条渐近线m:
,一条渐近线m: ,设过点A
,设过点A 的直线l的方向向量
的直线l的方向向量 .
.
(1)求双曲线C的方程;
(2)若过原点的直线 ,且a与l的距离为
,且a与l的距离为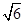 ,求K的值;
,求K的值;
(3)证明:当 时,在双曲线C的右支上不存在点Q,使之到直线l的距离为
时,在双曲线C的右支上不存在点Q,使之到直线l的距离为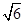 .
.
已知双曲线C的中心是原点,右焦点为F
 ,一条渐近线m:
,一条渐近线m: ,设过点A
,设过点A 的直线l的方向向量
的直线l的方向向量 .
.(1)求双曲线C的方程;
(2)若过原点的直线
 ,且a与l的距离为
,且a与l的距离为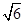 ,求K的值;
,求K的值;(3)证明:当
 时,在双曲线C的右支上不存在点Q,使之到直线l的距离为
时,在双曲线C的右支上不存在点Q,使之到直线l的距离为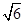 .
. 搜索
搜索
 难度系数:0.94
难度系数:0.94  答案解析
答案解析
 有奖纠错
有奖纠错
