全一卷
1.设x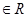 ,则不等式
,则不等式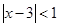 的解集为
的解集为______________________ .
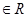 ,则不等式
,则不等式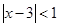 的解集为
的解集为2.设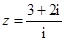 ,其中
,其中 为虚数单位,则
为虚数单位,则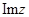 =_____________.
=_____________.
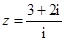 ,其中
,其中 为虚数单位,则
为虚数单位,则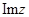 =_____________.
=_____________.3.已知平行直线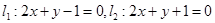 ,则l1与l2的距离是_____________.
,则l1与l2的距离是_____________.
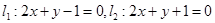 ,则l1与l2的距离是_____________.
,则l1与l2的距离是_____________.4.某次体检,6位同学的身高(单位:米)分别为1.72,1.78,1.75,1.80,1.69,1.77,则这组数据的中位数是_________(米).
5.已知点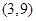 在函数
在函数 的图像上,则
的图像上,则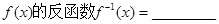 .
.
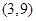 在函数
在函数 的图像上,则
的图像上,则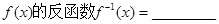 .
.6.如图,在正四棱柱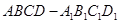 中,底面
中,底面 的边长为3,
的边长为3,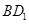 与底面所成的角的大小为
与底面所成的角的大小为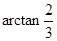 ,则该正四棱柱的高等于____________.
,则该正四棱柱的高等于____________.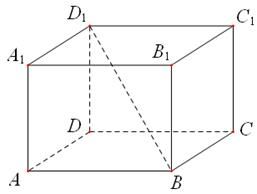
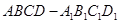 中,底面
中,底面 的边长为3,
的边长为3,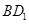 与底面所成的角的大小为
与底面所成的角的大小为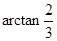 ,则该正四棱柱的高等于____________.
,则该正四棱柱的高等于____________.
7.方程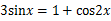 在区间
在区间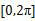 上的解为___________ .
上的解为___________ .
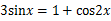 在区间
在区间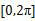 上的解为___________ .
上的解为___________ .8.在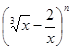 的二项展开式中,所有项的二项式系数之和为256,则常数项等于_________.
的二项展开式中,所有项的二项式系数之和为256,则常数项等于_________.
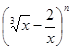 的二项展开式中,所有项的二项式系数之和为256,则常数项等于_________.
的二项展开式中,所有项的二项式系数之和为256,则常数项等于_________.9.已知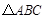 的三边长分别为3,5,7,则该三角形的外接圆半径等于_________.
的三边长分别为3,5,7,则该三角形的外接圆半径等于_________.
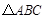 的三边长分别为3,5,7,则该三角形的外接圆半径等于_________.
的三边长分别为3,5,7,则该三角形的外接圆半径等于_________.10.设a>0,b>0. 若关于x,y的方程组 无解,则
无解,则 的取值范围是 .
的取值范围是 .
 无解,则
无解,则 的取值范围是 .
的取值范围是 .11.无穷数列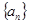 由k个不同的数组成,
由k个不同的数组成,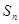 为
为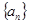 的前n项和.若对任意
的前n项和.若对任意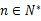 ,
,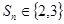 ,则k的最大值为________.
,则k的最大值为________.
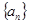 由k个不同的数组成,
由k个不同的数组成,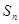 为
为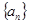 的前n项和.若对任意
的前n项和.若对任意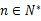 ,
,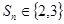 ,则k的最大值为________.
,则k的最大值为________.12.在平面直角坐标系中,已知A(1,0),B(0,−1),P是曲线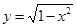 上一个动点,则
上一个动点,则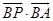 的取值范围是
的取值范围是_____________ .
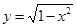 上一个动点,则
上一个动点,则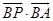 的取值范围是
的取值范围是13.设 .若对任意实数
.若对任意实数 都有
都有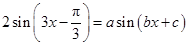 ,则满足条件的有序实数组
,则满足条件的有序实数组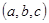 的组数为
的组数为_______ .
 .若对任意实数
.若对任意实数 都有
都有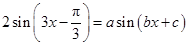 ,则满足条件的有序实数组
,则满足条件的有序实数组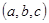 的组数为
的组数为14.如图,在平面直角坐标系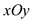 中,O为正八边形
中,O为正八边形 的中心,
的中心, .任取不同的两点
.任取不同的两点 ,点P满足
,点P满足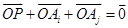 ,则点P落在第一象限的概率是_____________.
,则点P落在第一象限的概率是_____________.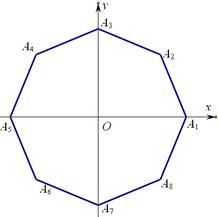
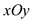 中,O为正八边形
中,O为正八边形 的中心,
的中心, .任取不同的两点
.任取不同的两点 ,点P满足
,点P满足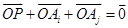 ,则点P落在第一象限的概率是_____________.
,则点P落在第一象限的概率是_____________.
15.设
 R,则“
R,则“ >1”是“
>1”是“ >1”的
>1”的

 R,则“
R,则“ >1”是“
>1”是“ >1”的
>1”的| A.充分不必要条件 |
| B.必要不充分条件 |
| C.充要条件 |
| D.既不充分也不必要条件 |
16.下列极坐标方程中,对应的曲线为如图的是().
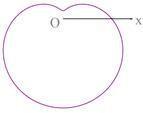

A. | B. |
C. | D. |
17.已知无穷等比数列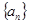 的公比为
的公比为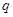 ,前n项和为
,前n项和为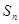 ,且
,且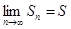 .下列条件中,使得
.下列条件中,使得 恒成立的是().
恒成立的是().
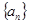 的公比为
的公比为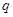 ,前n项和为
,前n项和为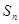 ,且
,且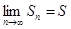 .下列条件中,使得
.下列条件中,使得 恒成立的是().
恒成立的是().A. |
B. |
C. |
D. |
18.设 、
、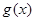 、
、 是定义域为R的三个函数,对于命题:①若
是定义域为R的三个函数,对于命题:①若 、
、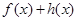 、
、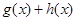 均是增函数,则
均是增函数,则 、
、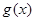 、
、 中至少有一个增函数;②若
中至少有一个增函数;②若 、
、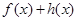 、
、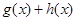 均是以
均是以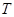 为周期的函数,则
为周期的函数,则 、
、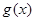 、
、 均是以
均是以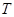 为周期的函数,下列判断正确的是( ).
为周期的函数,下列判断正确的是( ).
 、
、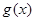 、
、 是定义域为R的三个函数,对于命题:①若
是定义域为R的三个函数,对于命题:①若 、
、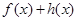 、
、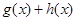 均是增函数,则
均是增函数,则 、
、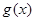 、
、 中至少有一个增函数;②若
中至少有一个增函数;②若 、
、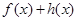 、
、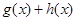 均是以
均是以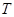 为周期的函数,则
为周期的函数,则 、
、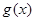 、
、 均是以
均是以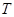 为周期的函数,下列判断正确的是( ).
为周期的函数,下列判断正确的是( ).| A.①和②均为真命题 |
| B.①和②均为假命题 |
| C.①为真命题,②为假命题 |
| D.①为假命题,②为真命题 |
19.本题共有2个小题,第一小题满分6分,第二小题满分6分.
将边长为1的正方形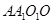 (及其内部)绕的
(及其内部)绕的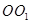 旋转一周形成圆柱,如图,
旋转一周形成圆柱,如图,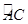 长为
长为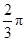 ,
,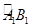 长为
长为 ,其中
,其中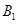 与
与 在平面
在平面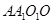 的同侧.
的同侧.
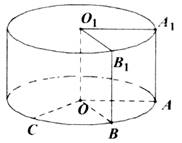
(1)求三棱锥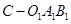 的体积;
的体积;
(2)求异面直线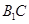 与
与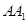 所成的角的大小.
所成的角的大小.
将边长为1的正方形
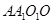 (及其内部)绕的
(及其内部)绕的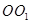 旋转一周形成圆柱,如图,
旋转一周形成圆柱,如图,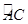 长为
长为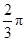 ,
,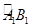 长为
长为 ,其中
,其中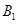 与
与 在平面
在平面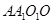 的同侧.
的同侧.
(1)求三棱锥
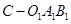 的体积;
的体积;(2)求异面直线
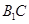 与
与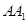 所成的角的大小.
所成的角的大小.20.有一块正方形菜地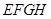 ,
,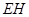 所在直线是一条小河.收获的蔬菜可送到
所在直线是一条小河.收获的蔬菜可送到 点或河边运走.于是,菜地分为两个区域
点或河边运走.于是,菜地分为两个区域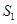 和
和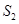 ,其中
,其中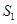 中的蔬菜运到河边较近,
中的蔬菜运到河边较近,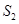 中的蔬菜运到
中的蔬菜运到 点较近,而菜地内
点较近,而菜地内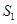 和
和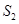 的分界线
的分界线 上的点到河边与到
上的点到河边与到 点的距离相等,现建立平面直角坐标系,其中原点
点的距离相等,现建立平面直角坐标系,其中原点 为
为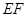 的中点,点
的中点,点 的坐标为(1,0),如图.
的坐标为(1,0),如图.
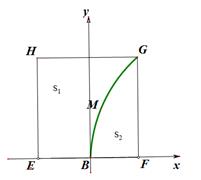
(1)求菜地内的分界线 的方程;
的方程;
(2)菜农从蔬菜运量估计出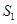 面积是
面积是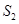 面积的两倍,由此得到
面积的两倍,由此得到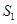 面积的“经验值”为
面积的“经验值”为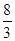 .设
.设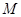 是
是 上纵坐标为1的点,请计算以
上纵坐标为1的点,请计算以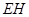 为一边、另有一边过点
为一边、另有一边过点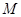 的矩形的面积,及五边形
的矩形的面积,及五边形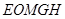 的面积,并判断哪一个更接近于
的面积,并判断哪一个更接近于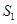 面积的经验值.
面积的经验值.
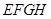 ,
,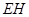 所在直线是一条小河.收获的蔬菜可送到
所在直线是一条小河.收获的蔬菜可送到 点或河边运走.于是,菜地分为两个区域
点或河边运走.于是,菜地分为两个区域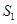 和
和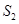 ,其中
,其中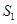 中的蔬菜运到河边较近,
中的蔬菜运到河边较近,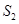 中的蔬菜运到
中的蔬菜运到 点较近,而菜地内
点较近,而菜地内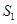 和
和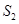 的分界线
的分界线 上的点到河边与到
上的点到河边与到 点的距离相等,现建立平面直角坐标系,其中原点
点的距离相等,现建立平面直角坐标系,其中原点 为
为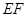 的中点,点
的中点,点 的坐标为(1,0),如图.
的坐标为(1,0),如图.
(1)求菜地内的分界线
 的方程;
的方程;(2)菜农从蔬菜运量估计出
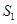 面积是
面积是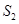 面积的两倍,由此得到
面积的两倍,由此得到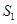 面积的“经验值”为
面积的“经验值”为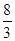 .设
.设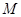 是
是 上纵坐标为1的点,请计算以
上纵坐标为1的点,请计算以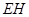 为一边、另有一边过点
为一边、另有一边过点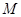 的矩形的面积,及五边形
的矩形的面积,及五边形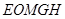 的面积,并判断哪一个更接近于
的面积,并判断哪一个更接近于 面积的经验值.
面积的经验值.21.双曲线 的左、右焦点分别为
的左、右焦点分别为 ,直线
,直线 过
过 且与双曲线交于
且与双曲线交于 两点.
两点.
(1)若 的倾斜角为
的倾斜角为 ,
, 是等边三角形,求双曲线的渐近线方程;
是等边三角形,求双曲线的渐近线方程;
(2)设 ,若
,若 的斜率存在,且
的斜率存在,且 ,求
,求 的斜率.
的斜率.
 的左、右焦点分别为
的左、右焦点分别为 ,直线
,直线 过
过 且与双曲线交于
且与双曲线交于 两点.
两点.(1)若
 的倾斜角为
的倾斜角为 ,
, 是等边三角形,求双曲线的渐近线方程;
是等边三角形,求双曲线的渐近线方程;(2)设
 ,若
,若 的斜率存在,且
的斜率存在,且 ,求
,求 的斜率.
的斜率.22.已知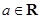 ,函数
,函数 .
.
(1)当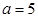 时,解不等式
时,解不等式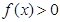 ;
;
(2)若关于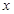 的方程
的方程 的解集中恰好有一个元素,求
的解集中恰好有一个元素,求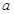 的取值范围;
的取值范围;
(3)设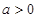 ,若对任意
,若对任意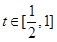 ,函数
,函数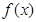 在区间
在区间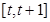 上的最大值与最小值的差不超过1,求
上的最大值与最小值的差不超过1,求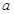 的取值范围.
的取值范围.
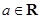 ,函数
,函数 .
.(1)当
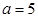 时,解不等式
时,解不等式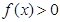 ;
;(2)若关于
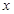 的方程
的方程 的解集中恰好有一个元素,求
的解集中恰好有一个元素,求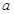 的取值范围;
的取值范围;(3)设
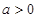 ,若对任意
,若对任意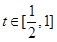 ,函数
,函数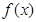 在区间
在区间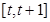 上的最大值与最小值的差不超过1,求
上的最大值与最小值的差不超过1,求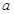 的取值范围.
的取值范围.23.若无穷数列 满足:只要
满足:只要 ,必有
,必有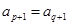 ,则称
,则称 具有性质
具有性质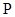 .
.
(1)若 具有性质
具有性质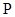 ,且
,且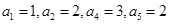 ,
, ,求
,求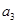 ;
;
(2)若无穷数列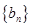 是等差数列,无穷数列
是等差数列,无穷数列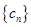 是公比为正数的等比数列,
是公比为正数的等比数列,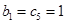 ,
,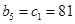 ,
,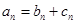 ,判断
,判断 是否具有性质
是否具有性质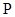 ,并说明理由;
,并说明理由;
(3)设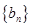 是无穷数列,已知
是无穷数列,已知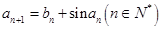 .求证:“对任意
.求证:“对任意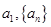 都具有性质
都具有性质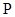 ”的充要条件为“
”的充要条件为“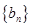 是常数列”.
是常数列”.
 满足:只要
满足:只要 ,必有
,必有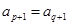 ,则称
,则称 具有性质
具有性质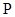 .
.(1)若
 具有性质
具有性质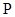 ,且
,且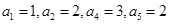 ,
, ,求
,求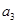 ;
;(2)若无穷数列
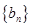 是等差数列,无穷数列
是等差数列,无穷数列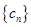 是公比为正数的等比数列,
是公比为正数的等比数列,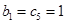 ,
,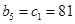 ,
,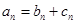 ,判断
,判断 是否具有性质
是否具有性质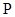 ,并说明理由;
,并说明理由;(3)设
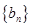 是无穷数列,已知
是无穷数列,已知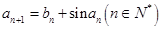 .求证:“对任意
.求证:“对任意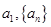 都具有性质
都具有性质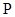 ”的充要条件为“
”的充要条件为“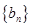 是常数列”.
是常数列”. 搜索
搜索
 难度系数:0.64
难度系数:0.64  答案解析
答案解析
 有奖纠错
有奖纠错
