全一卷
1.汽车经过启动、加速行驶、匀速行驶、减速行驶之后停车,若把这一过程中汽车的行驶路程 看作时间
看作时间 的函数,其图象可能是( )
的函数,其图象可能是( )
 看作时间
看作时间 的函数,其图象可能是( )
的函数,其图象可能是( )
2.若直线 通过点
通过点 ,则
,则
 通过点
通过点 ,则
,则A. | B. | C. | D. |
3.在 中,
中, ,
, .若点
.若点 满足
满足 ,则
,则 ()
()
 中,
中, ,
, .若点
.若点 满足
满足 ,则
,则 ()
()A. | B. | C. | D. |
4.为得到函数 的图象,只需将函数
的图象,只需将函数 的图象( )
的图象( )
 的图象,只需将函数
的图象,只需将函数 的图象( )
的图象( )A.向左平移 个单位 个单位 | B.向右平移 个单位 个单位 |
C.向左平移 个单位 个单位 | D.向右平移 个单位 个单位 |
5.函数 的定义域为
的定义域为
 的定义域为
的定义域为A. | B. |
C. | D. |
6.设 ,且
,且 为正实数,则
为正实数,则
 ,且
,且 为正实数,则
为正实数,则
| A.2 | B.1 | C.0 | D. |
7.已知等差数列 满足
满足 ,
, ,则它的前10项的和
,则它的前10项的和
 满足
满足 ,
, ,则它的前10项的和
,则它的前10项的和
| A.138 | B.135 | C.95 | D.23 |
8.设曲线 在点
在点 处的切线与直线
处的切线与直线 垂直,则
垂直,则
 在点
在点 处的切线与直线
处的切线与直线 垂直,则
垂直,则
| A.2 | B. | C. | D. |
9.设奇函数 在
在 上为增函数,且
上为增函数,且 ,则不等式
,则不等式 的解集为
的解集为
 在
在 上为增函数,且
上为增函数,且 ,则不等式
,则不等式 的解集为
的解集为A. | B. |
C. | D. |
10.已知三棱柱 的侧棱与底面边长都相等,
的侧棱与底面边长都相等, 在底面
在底面 内的射影为
内的射影为 的中心,则
的中心,则 与底面
与底面 所成角的正弦值等于( )
所成角的正弦值等于( )
 的侧棱与底面边长都相等,
的侧棱与底面边长都相等, 在底面
在底面 内的射影为
内的射影为 的中心,则
的中心,则 与底面
与底面 所成角的正弦值等于( )
所成角的正弦值等于( )A. | B. | C. | D. |
11.如图,一环形花坛分成 四块,现有4种不同的花供选种,要求在每块里种1种花,且相邻的2块种不同的花,则不同的种法总数为
四块,现有4种不同的花供选种,要求在每块里种1种花,且相邻的2块种不同的花,则不同的种法总数为

 四块,现有4种不同的花供选种,要求在每块里种1种花,且相邻的2块种不同的花,则不同的种法总数为
四块,现有4种不同的花供选种,要求在每块里种1种花,且相邻的2块种不同的花,则不同的种法总数为
| A.96 | B.84 | C.60 | D.48 |
12.若函数 的图像与函数
的图像与函数 的图像关于直线
的图像关于直线 对称,则
对称,则 ( )
( )
 的图像与函数
的图像与函数 的图像关于直线
的图像关于直线 对称,则
对称,则 ( )
( )A. | B. | C. | D. |
13.已知函数 ,
, .
.
(Ⅰ)讨论函数 的单调区间;
的单调区间;
(Ⅱ)设函数 在区间
在区间 内是减函数,求
内是减函数,求 的取值范围.
的取值范围.
 ,
, .
.(Ⅰ)讨论函数
 的单调区间;
的单调区间;(Ⅱ)设函数
 在区间
在区间 内是减函数,求
内是减函数,求 的取值范围.
的取值范围.14.双曲线的中心为原点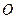 ,焦点在
,焦点在 轴上,两条渐近线分别为
轴上,两条渐近线分别为 ,经过右焦点
,经过右焦点 垂直于
垂直于 的直线分别交
的直线分别交 于
于 两点.已知
两点.已知 成等差数列,且
成等差数列,且 与
与 同向.
同向.
(Ⅰ)求双曲线的离心率;
(Ⅱ)设 被双曲线所截得的线段的长为4,求双曲线的方程.
被双曲线所截得的线段的长为4,求双曲线的方程.
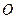 ,焦点在
,焦点在 轴上,两条渐近线分别为
轴上,两条渐近线分别为 ,经过右焦点
,经过右焦点 垂直于
垂直于 的直线分别交
的直线分别交 于
于 两点.已知
两点.已知 成等差数列,且
成等差数列,且 与
与 同向.
同向.(Ⅰ)求双曲线的离心率;
(Ⅱ)设
 被双曲线所截得的线段的长为4,求双曲线的方程.
被双曲线所截得的线段的长为4,求双曲线的方程.15.已知5只动物中有1只患有某种疾病,需要通过化验血液来确定患病的动物.血液化验结果呈阳性的即为患病动物,呈阴性的即没患病.下面是两种化验方案:
方案甲:逐个化验,直到能确定患病动物为止.
方案乙:先任取3只,将它们的血液混在一起化验.若结果呈阳性则表明患病动物为这3只中的1只,然后再逐个化验,直到能确定患病动物为止;若结果呈阴性则在另外2只中任取1只化验.
(1)求依方案甲所需化验次数不少于依方案乙所需化验次数的概率;
(2) 表示依方案乙所需化验次数,求
表示依方案乙所需化验次数,求 的期望.
的期望.
方案甲:逐个化验,直到能确定患病动物为止.
方案乙:先任取3只,将它们的血液混在一起化验.若结果呈阳性则表明患病动物为这3只中的1只,然后再逐个化验,直到能确定患病动物为止;若结果呈阴性则在另外2只中任取1只化验.
(1)求依方案甲所需化验次数不少于依方案乙所需化验次数的概率;
(2)
 表示依方案乙所需化验次数,求
表示依方案乙所需化验次数,求 的期望.
的期望.16.设 的内角
的内角 所对的边长分别为
所对的边长分别为 ,且
,且 .
.
(Ⅰ)求 的值;(Ⅱ)求
的值;(Ⅱ)求 的最大值.
的最大值.
 的内角
的内角 所对的边长分别为
所对的边长分别为 ,且
,且 .
.(Ⅰ)求
 的值;(Ⅱ)求
的值;(Ⅱ)求 的最大值.
的最大值.17.
(注意:在试题卷上作答无效)
四棱锥 中,底面
中,底面 为矩形,侧面
为矩形,侧面 底面
底面 ,
, ,
, ,
, .
.
(Ⅰ)证明: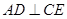 ;
;
(Ⅱ)设 与平面
与平面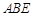 所成的角为
所成的角为 ,求二面角
,求二面角 的大小.
的大小.
(注意:在试题卷上作答无效)
四棱锥
 中,底面
中,底面 为矩形,侧面
为矩形,侧面 底面
底面 ,
, ,
, ,
, .
.(Ⅰ)证明:
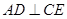 ;
;(Ⅱ)设
 与平面
与平面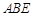 所成的角为
所成的角为 ,求二面角
,求二面角 的大小.
的大小.
18.设函数 .数列
.数列  满足
满足 ,
,  .
.
(Ⅰ)证明:函数 在区间
在区间  是增函数;
是增函数;
(Ⅱ)证明: ;
;
(Ⅲ)设 ,整数
,整数  .证明:
.证明: .
.
 .数列
.数列  满足
满足 ,
,  .
.(Ⅰ)证明:函数
 在区间
在区间  是增函数;
是增函数;(Ⅱ)证明:
 ;
;(Ⅲ)设
 ,整数
,整数  .证明:
.证明: .
.19.若 满足约束条件
满足约束条件 则
则 的最大值为 。
的最大值为 。
 满足约束条件
满足约束条件 则
则 的最大值为 。
的最大值为 。20.已知抛物线 的焦点是坐标原点,则以抛物线与两坐标轴的三个交点为顶点的三角形面积为 。
的焦点是坐标原点,则以抛物线与两坐标轴的三个交点为顶点的三角形面积为 。
 的焦点是坐标原点,则以抛物线与两坐标轴的三个交点为顶点的三角形面积为 。
的焦点是坐标原点,则以抛物线与两坐标轴的三个交点为顶点的三角形面积为 。21.在 中,
中, ,
, 。若以
。若以 为焦点的椭圆经过点
为焦点的椭圆经过点 ,则该椭圆的离心率
,则该椭圆的离心率 。
。
 中,
中, ,
, 。若以
。若以 为焦点的椭圆经过点
为焦点的椭圆经过点 ,则该椭圆的离心率
,则该椭圆的离心率 。
。22.等边三角形 与正方形
与正方形 有一公共边
有一公共边 ,二面角
,二面角 的余弦值为
的余弦值为 ,
, 分别是
分别是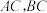 的中点,则
的中点,则 所成角的余弦值等于 .
所成角的余弦值等于 .
 与正方形
与正方形 有一公共边
有一公共边 ,二面角
,二面角 的余弦值为
的余弦值为 ,
, 分别是
分别是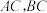 的中点,则
的中点,则 所成角的余弦值等于 .
所成角的余弦值等于 . 搜索
搜索
 难度系数:0.94
难度系数:0.94  答案解析
答案解析
 有奖纠错
有奖纠错
