全一卷
1.异面直线 、
、 分别在平面
分别在平面 、
、 内,若
内,若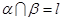 ,则直线
,则直线 必定是( )
必定是( )
 、
、 分别在平面
分别在平面 、
、 内,若
内,若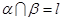 ,则直线
,则直线 必定是( )
必定是( )A.分别与 、 、 相交 相交 | B.与 、 、 都不相交 都不相交 |
C.至少与 、 、 中之一相交 中之一相交 | D.至多与 、 、 中之一相交 中之一相交 |
2.设动点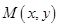 到点
到点 的距离与到直线
的距离与到直线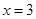 的距离之比为2,则
的距离之比为2,则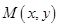 的轨迹方程为()
的轨迹方程为()
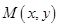 到点
到点 的距离与到直线
的距离与到直线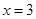 的距离之比为2,则
的距离之比为2,则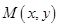 的轨迹方程为()
的轨迹方程为()A. | B. |
C. . . | D. . . |
3.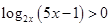 的充要条件是()
的充要条件是()
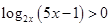 的充要条件是()
的充要条件是()A. | B. 或 或 |
C. | D. <或 <或 |
4.函数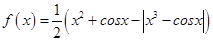 的图象(图中实线部分)是()
的图象(图中实线部分)是()
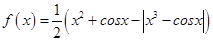 的图象(图中实线部分)是()
的图象(图中实线部分)是()A. | B. |
C. | D. |
5.已知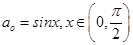 ,
,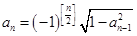 ,且
,且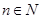 ,
,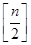 是
是 的整数部分,则
的整数部分,则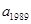 等于( )
等于( )
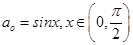 ,
,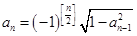 ,且
,且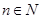 ,
,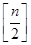 是
是 的整数部分,则
的整数部分,则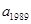 等于( )
等于( )A. | B. | C. | D. |
6.设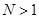 ,且
,且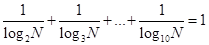 ,那么
,那么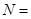 ______.
______.
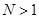 ,且
,且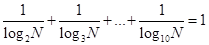 ,那么
,那么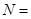 ______.
______.7.设椭圆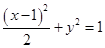 的两个焦点为
的两个焦点为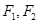 ,其短轴上的一个顶点为A,那么
,其短轴上的一个顶点为A,那么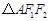 的外接圆的方程为______.
的外接圆的方程为______.
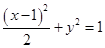 的两个焦点为
的两个焦点为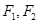 ,其短轴上的一个顶点为A,那么
,其短轴上的一个顶点为A,那么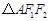 的外接圆的方程为______.
的外接圆的方程为______.8.若一圆台的上底周长为4,下底周长为9,平行于底的截面周长是上、下底周长的比例中项,则这个截面分圆台的高所成的两段的比为______.
9.设关于 的方程
的方程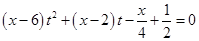 无实根,那么函数
无实根,那么函数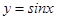 的反函数是______.
的反函数是______.
 的方程
的方程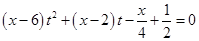 无实根,那么函数
无实根,那么函数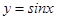 的反函数是______.
的反函数是______.10.已知由幂函数构成的集合A中,奇函数有10个,定义在区间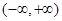 上的增函数有8个,图象过原点的函数有12个,那么集合A的元素最多有______个.
上的增函数有8个,图象过原点的函数有12个,那么集合A的元素最多有______个.
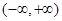 上的增函数有8个,图象过原点的函数有12个,那么集合A的元素最多有______个.
上的增函数有8个,图象过原点的函数有12个,那么集合A的元素最多有______个.11.已知: 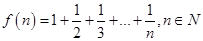 .求证:
.求证:
(1)若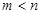 ,且
,且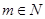 ,则
,则 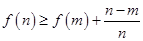
(2)当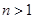 时,
时,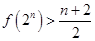 .
.
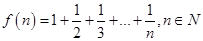 .求证:
.求证:(1)若
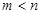 ,且
,且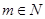 ,则
,则 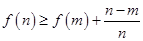
(2)当
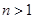 时,
时,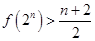 .
.12.如图,已知三棱柱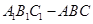 的底面是边长为2的正三角形,侧棱
的底面是边长为2的正三角形,侧棱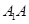 与下底面相邻的两边AB,AC均成45度的角.
与下底面相邻的两边AB,AC均成45度的角.
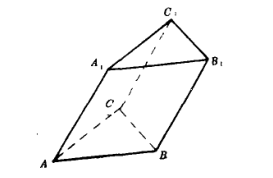
(1)求点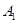 到平面B1BCC1的距离.
到平面B1BCC1的距离.
(2)试问,当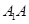 为多长时,点
为多长时,点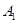 到平面
到平面 与到平面
与到平面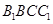 的距离相等.
的距离相等.
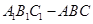 的底面是边长为2的正三角形,侧棱
的底面是边长为2的正三角形,侧棱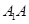 与下底面相邻的两边AB,AC均成45度的角.
与下底面相邻的两边AB,AC均成45度的角.
(1)求点
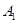 到平面B1BCC1的距离.
到平面B1BCC1的距离.(2)试问,当
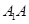 为多长时,点
为多长时,点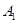 到平面
到平面 与到平面
与到平面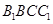 的距离相等.
的距离相等.13.设G是紧夹在平行线 与
与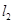 之间的任一凸区域(即其边界上任意两点之间所连线段都包含于它的区域),其边界
之间的任一凸区域(即其边界上任意两点之间所连线段都包含于它的区域),其边界 与
与 和
和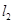 都有公共点.平行于
都有公共点.平行于 的直线
的直线 将G分为如图所示的
将G分为如图所示的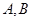 两部分,且l与
两部分,且l与 和
和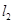 之间的距离分别为a和b.
之间的距离分别为a和b.
(1)G为怎样的图形时;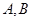 两部分的面积之比
两部分的面积之比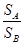 达到最大?并说明理由.
达到最大?并说明理由.
(2)试求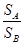 的最大值.
的最大值.
 与
与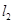 之间的任一凸区域(即其边界上任意两点之间所连线段都包含于它的区域),其边界
之间的任一凸区域(即其边界上任意两点之间所连线段都包含于它的区域),其边界 与
与 和
和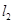 都有公共点.平行于
都有公共点.平行于 的直线
的直线 将G分为如图所示的
将G分为如图所示的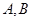 两部分,且l与
两部分,且l与 和
和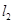 之间的距离分别为a和b.
之间的距离分别为a和b.(1)G为怎样的图形时;
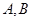 两部分的面积之比
两部分的面积之比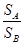 达到最大?并说明理由.
达到最大?并说明理由.(2)试求
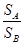 的最大值.
的最大值.14.已知数列 满足
满足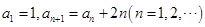 ,
,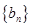 满足
满足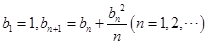 .证明:
.证明: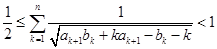 .
.
 满足
满足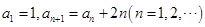 ,
,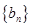 满足
满足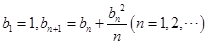 .证明:
.证明: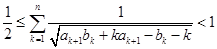 .
. 搜索
搜索
 难度系数:0.65
难度系数:0.65  答案解析
答案解析
 有奖纠错
有奖纠错
