全一卷
1.-2的绝对值是( )
| A.2 | B. | C. | D. |
2.下列立体图形中,主视图是圆的是( )
A. | B. | C. | D. |
3.下列计算正确的是( )
A. | B. | C. | D. |
4.如图,平行线 ,
, 被直线
被直线 所截,
所截, 平分
平分 ,若
,若 ,则
,则 的度数是( )
的度数是( )

 ,
, 被直线
被直线 所截,
所截, 平分
平分 ,若
,若 ,则
,则 的度数是( )
的度数是( )
A. | B. | C. | D. |
5.六边形的内角和是( )
| A.180° | B.360° | C.540° | D.720° |
6.不等式 的解集是( )
的解集是( )
 的解集是( )
的解集是( )A. | B. | C. | D. |
7.一家鞋店在一段时间内销售了某种女鞋20双,各种尺码鞋的销售量如表所示.
则所销售的女鞋尺码的众数是( )
尺码/ | 22.5 | 23 | 23.5 | 24 | 24.5 |
销售量/双 | 1 | 4 | 6 | 8 | 1 |
A. | B. | C. | D. |
8.若关于x的一元二次方程 有两个相等的实数根,则c的值是( )
有两个相等的实数根,则c的值是( )
 有两个相等的实数根,则c的值是( )
有两个相等的实数根,则c的值是( )| A.36 | B.9 | C.6 | D. |
9.如图,在 中,
中, ,分别以点A和点C为圆心,大于
,分别以点A和点C为圆心,大于 的长为半径作弧,两弧相交于M,N两点,作直线
的长为半径作弧,两弧相交于M,N两点,作直线 ,直线
,直线 与
与 相交于点D,连接
相交于点D,连接 ,若
,若 ,则
,则 的长是( )
的长是( )

 中,
中, ,分别以点A和点C为圆心,大于
,分别以点A和点C为圆心,大于 的长为半径作弧,两弧相交于M,N两点,作直线
的长为半径作弧,两弧相交于M,N两点,作直线 ,直线
,直线 与
与 相交于点D,连接
相交于点D,连接 ,若
,若 ,则
,则 的长是( )
的长是( )
| A.6 | B.3 | C.1.5 | D.1 |
10.汽车油箱中有汽油 ,如果不再加油,那么油箱中的油量y(单位:L)随行驶路程x(单位:
,如果不再加油,那么油箱中的油量y(单位:L)随行驶路程x(单位: )的增加而减少,平均耗油量为
)的增加而减少,平均耗油量为 .当
.当 时,y与x的函数解析式是( )
时,y与x的函数解析式是( )
 ,如果不再加油,那么油箱中的油量y(单位:L)随行驶路程x(单位:
,如果不再加油,那么油箱中的油量y(单位:L)随行驶路程x(单位: )的增加而减少,平均耗油量为
)的增加而减少,平均耗油量为 .当
.当 时,y与x的函数解析式是( )
时,y与x的函数解析式是( )A. | B. | C. | D. |
11.方程 的解是
的解是_______ .
 的解是
的解是12.不透明袋子中装有2个黑球,3个白球,这些球除了颜色外无其他差别,从袋子中随机摸出1个球,“摸出黑球”的概率是_______ .
13.如图,在平面直角坐标系中,点A的坐标是 ,将线段
,将线段 向右平移4个单位长度,得到线段
向右平移4个单位长度,得到线段 ,点A的对应点C的坐标是
,点A的对应点C的坐标是_______ .

 ,将线段
,将线段 向右平移4个单位长度,得到线段
向右平移4个单位长度,得到线段 ,点A的对应点C的坐标是
,点A的对应点C的坐标是
14.如图,正方形 的边长是
的边长是 ,将对角线
,将对角线 绕点A顺时针旋转
绕点A顺时针旋转 的度数,点C旋转后的对应点为E,则
的度数,点C旋转后的对应点为E,则 的长是
的长是____________ (结果保留 ).
).

 的边长是
的边长是 ,将对角线
,将对角线 绕点A顺时针旋转
绕点A顺时针旋转 的度数,点C旋转后的对应点为E,则
的度数,点C旋转后的对应点为E,则 的长是
的长是 ).
).
15.我国古代著作《九章算术》中记载了这样一个问题:“今有共买豕,人出一百,盈一百;人出九十,适足.”其大意是:“今有人合伙买猪,每人出100钱,则会多出100钱;每人出90钱,恰好合适.”若设共有x人,根据题意,可列方程为____________ .
16.如图,对折矩形纸片 ,使得
,使得 与
与 重合,得到折痕
重合,得到折痕 ,把纸片展平,再一次折叠纸片,使点A的对应点
,把纸片展平,再一次折叠纸片,使点A的对应点 落在
落在 上,并使折痕经过点B,得到折痕
上,并使折痕经过点B,得到折痕 .连接
.连接 ,若
,若 ,
, ,则
,则 的长是
的长是____________  .
.

 ,使得
,使得 与
与 重合,得到折痕
重合,得到折痕 ,把纸片展平,再一次折叠纸片,使点A的对应点
,把纸片展平,再一次折叠纸片,使点A的对应点 落在
落在 上,并使折痕经过点B,得到折痕
上,并使折痕经过点B,得到折痕 .连接
.连接 ,若
,若 ,
, ,则
,则 的长是
的长是 .
.
17.计算 .
.
 .
.18.为了解某初级中学落实《中共中央国务院关于全面加强新时代大中小学劳动教育的意见》的实施情况,调查组从该校全体学生中随机抽取部分学生,调查他们平均每周劳动时间t(单位:h),并对数据进行整理,描述和分析,以下是根据调查结果绘制的统计图表的一部分.
平均每周劳动时间频数统计表

根据以上信息,回答下列问题∶
(1)填空: ______,
______, ______,
______, _____;
_____;
(2)若该校有1000名学生,请估计平均每周劳动时间在 范围内的学生人数.
范围内的学生人数.
平均每周劳动时间频数统计表
平均每周劳动时间 | 频数 | 频率 |
| 3 | |
| a | 0.12 |
| 37 | b |
| 0.35 | |
| ||
合计 | c |

根据以上信息,回答下列问题∶
(1)填空:
 ______,
______, ______,
______, _____;
_____;(2)若该校有1000名学生,请估计平均每周劳动时间在
 范围内的学生人数.
范围内的学生人数.19.如图,四边形 是菱形,点E,F分别在
是菱形,点E,F分别在 上,
上, .求证
.求证 .
.

 是菱形,点E,F分别在
是菱形,点E,F分别在 上,
上, .求证
.求证 .
.
20.2022年北京冬奥会吉祥物冰墩墩和冬残奥会吉祥物雪容融深受大家喜爱.已知购买1个冰墩墩毛绒玩具和2个雪容融毛绒玩具用了400元,购买3个冰墩墩毛绒玩具和4个雪容融毛绒玩具用了1000元.这两种毛绒玩具的单价各是多少元?
21.密闭容器内有一定质量的二氧化碳,当容器的体积V(单位: )变化时,气体的密度
)变化时,气体的密度 (单位:
(单位: )随之变化.已知密度
)随之变化.已知密度 与体积V是反比例函数关系,它的图象如图所示,当
与体积V是反比例函数关系,它的图象如图所示,当 时,
时, .
.

(1)求密度 关于体积V的函数解析式;
关于体积V的函数解析式;
(2)若 ,求二氧化碳密度
,求二氧化碳密度 的变化范围.
的变化范围.
 )变化时,气体的密度
)变化时,气体的密度 (单位:
(单位: )随之变化.已知密度
)随之变化.已知密度 与体积V是反比例函数关系,它的图象如图所示,当
与体积V是反比例函数关系,它的图象如图所示,当 时,
时, .
.
(1)求密度
 关于体积V的函数解析式;
关于体积V的函数解析式;(2)若
 ,求二氧化碳密度
,求二氧化碳密度 的变化范围.
的变化范围.22.如图,莲花山是大连著名的景点之一,游客可以从山底乘坐索道车到达山项,索速车运行的速度是1米/秒,小明要测量莲花山山顶白塔的高度,他在索道A处测得白塔底部B的仰角的为 ,测得白塔顶部C的仰角的为
,测得白塔顶部C的仰角的为 .索道车从A处运行到B处所用时间的为5分钟.
.索道车从A处运行到B处所用时间的为5分钟.

(1)索道车从A处运行到B处的距离约为________米;
(2)请你利用小明测量的数据,求白塔 的高度(结果取整数).(参考数据:
的高度(结果取整数).(参考数据: )
)
 ,测得白塔顶部C的仰角的为
,测得白塔顶部C的仰角的为 .索道车从A处运行到B处所用时间的为5分钟.
.索道车从A处运行到B处所用时间的为5分钟.
(1)索道车从A处运行到B处的距离约为________米;
(2)请你利用小明测量的数据,求白塔
 的高度(结果取整数).(参考数据:
的高度(结果取整数).(参考数据: )
)23. 是
是 的直径,C是
的直径,C是 上一点,
上一点, ,垂足为D,过点A作
,垂足为D,过点A作 的切线,与
的切线,与 的延长线相交于点E.
的延长线相交于点E.

(1)如图1,求证 ;
;
(2)如图2,连接 ,若
,若 的半径为2,
的半径为2, ,求
,求 的长.
的长.
 是
是 的直径,C是
的直径,C是 上一点,
上一点, ,垂足为D,过点A作
,垂足为D,过点A作 的切线,与
的切线,与 的延长线相交于点E.
的延长线相交于点E.
(1)如图1,求证
 ;
;(2)如图2,连接
 ,若
,若 的半径为2,
的半径为2, ,求
,求 的长.
的长.24.如图,在 中,
中,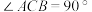 ,
, ,点D在
,点D在 上,
上, ,连接
,连接 ,
, ,点P是边
,点P是边 上一动点(点P不与点A,D,C重合),过点P作
上一动点(点P不与点A,D,C重合),过点P作 的垂线,与
的垂线,与 相交于点Q,连接
相交于点Q,连接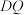 ,设
,设 ,
, 与
与 重叠部分的面积为S.
重叠部分的面积为S.

(1)求 的长;
的长;
(2)求S关于x的函数解析式,并直接写出自变量x的取值范围.
 中,
中,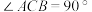 ,
, ,点D在
,点D在 上,
上, ,连接
,连接 ,
, ,点P是边
,点P是边 上一动点(点P不与点A,D,C重合),过点P作
上一动点(点P不与点A,D,C重合),过点P作 的垂线,与
的垂线,与 相交于点Q,连接
相交于点Q,连接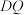 ,设
,设 ,
, 与
与 重叠部分的面积为S.
重叠部分的面积为S.
(1)求
 的长;
的长;(2)求S关于x的函数解析式,并直接写出自变量x的取值范围.
25.综合与实践
问题情境:
数学活动课上,王老师出示了一个问题:如图1,在 中,D是
中,D是 上一点,
上一点, .求证
.求证 .
.
独立思考:
(1)请解答王老师提出的问题.
实践探究:
(2)在原有问题条件不变的情况下,王老师增加下面的条件,并提出新问题,请你解答.“如图2,延长 至点E,使
至点E,使 ,
, 与
与 的延长线相交于点F,点G,H分别在
的延长线相交于点F,点G,H分别在 上,
上, ,
, .在图中找出与
.在图中找出与 相等的线段,并证明.”
相等的线段,并证明.”
问题解决:
(3)数学活动小组河学时上述问题进行特殊化研究之后发现,当 时,若给出
时,若给出 中任意两边长,则图3中所有已经用字母标记的线段长均可求,该小组提出下面的问题,请你解答.“如图3,在(2)的条件下,若
中任意两边长,则图3中所有已经用字母标记的线段长均可求,该小组提出下面的问题,请你解答.“如图3,在(2)的条件下,若 ,
,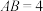 ,
, ,求
,求 的长.”
的长.”

问题情境:
数学活动课上,王老师出示了一个问题:如图1,在
 中,D是
中,D是 上一点,
上一点, .求证
.求证 .
.独立思考:
(1)请解答王老师提出的问题.
实践探究:
(2)在原有问题条件不变的情况下,王老师增加下面的条件,并提出新问题,请你解答.“如图2,延长
 至点E,使
至点E,使 ,
, 与
与 的延长线相交于点F,点G,H分别在
的延长线相交于点F,点G,H分别在 上,
上, ,
, .在图中找出与
.在图中找出与 相等的线段,并证明.”
相等的线段,并证明.”问题解决:
(3)数学活动小组河学时上述问题进行特殊化研究之后发现,当
 时,若给出
时,若给出 中任意两边长,则图3中所有已经用字母标记的线段长均可求,该小组提出下面的问题,请你解答.“如图3,在(2)的条件下,若
中任意两边长,则图3中所有已经用字母标记的线段长均可求,该小组提出下面的问题,请你解答.“如图3,在(2)的条件下,若 ,
,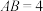 ,
, ,求
,求 的长.”
的长.”
26.在平面直角坐标系中,抛物线 与x轴相交于点A,B(点A在点B的左侧),与y轴相交于点C,连接
与x轴相交于点A,B(点A在点B的左侧),与y轴相交于点C,连接 .
.

(1)求点B,点C的坐标;
(2)如图1,点 在线段
在线段 上(点E不与点B重合),点F在y轴负半轴上,
上(点E不与点B重合),点F在y轴负半轴上, ,连接
,连接 ,设
,设 的面积为
的面积为 ,
, 的面积为
的面积为 ,
, ,当S取最大值时,求m的值;
,当S取最大值时,求m的值;
(3)如图2,抛物线的顶点为D,连接 ,点P在第一象限的抛物线上,
,点P在第一象限的抛物线上, 与
与 相交于点Q,是否存在点P,使
相交于点Q,是否存在点P,使 ,若存在,请求出点P的坐标;若不存在,请说明理由.
,若存在,请求出点P的坐标;若不存在,请说明理由.
 与x轴相交于点A,B(点A在点B的左侧),与y轴相交于点C,连接
与x轴相交于点A,B(点A在点B的左侧),与y轴相交于点C,连接 .
.
(1)求点B,点C的坐标;
(2)如图1,点
 在线段
在线段 上(点E不与点B重合),点F在y轴负半轴上,
上(点E不与点B重合),点F在y轴负半轴上, ,连接
,连接 ,设
,设 的面积为
的面积为 ,
, 的面积为
的面积为 ,
, ,当S取最大值时,求m的值;
,当S取最大值时,求m的值;(3)如图2,抛物线的顶点为D,连接
 ,点P在第一象限的抛物线上,
,点P在第一象限的抛物线上, 与
与 相交于点Q,是否存在点P,使
相交于点Q,是否存在点P,使 ,若存在,请求出点P的坐标;若不存在,请说明理由.
,若存在,请求出点P的坐标;若不存在,请说明理由. 搜索
搜索
 难度系数:0.94
难度系数:0.94  答案解析
答案解析
 有奖纠错
有奖纠错






