搜索
全一卷
难度系数：0.94 
答案解析
有奖纠错
1．﹣5的相反数是（ ）
| A．5 | B．﹣5 | C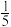． | D． |
2．2022年3月23日下午，“天宫课堂”第2课在中国空间站开讲，神舟十三号乘组三位航天员翟志刚、王亚平、叶光富进行授课，某平台进行全程直播．某一时刻观看人数达到3790000人．用科学记数法表示3790000，正确的是（ ）
A． | B． | C． | D． |
3．如图是由四个相同的小正方体组成的几何体，它的主视图是（ ）
A． | B． | C． | D． |
4．统计一名射击运动员在某次训练中10次射击的中靶环数，获得如下数据：7，8，10，9，9，8，10，9，9，10．这组数据的众数是（ ）
| A．7 | B．8 | C．9 | D．10 |
5．下列各式的运算，结果正确的是（ ）
A． | B． | C． | D． |
6．如图，将△ABC沿BC方向平移1cm得到对应的△A′B′C′．若B′C=2cm，则BC′的长是（ ）
| A．2cm | B．3cm | C．4cm | D．5cm |
7．把抛物线y=x2向上平移3个单位，平移后抛物线的表达式是( )
A．y= -3 | B．y=+3 | C．y= | D．y= |
8．如图，已知在锐角△ABC中，AB＝AC，AD是△ABC的角平分线，E是AD上一点，连结EB，EC．若∠EBC＝45°，BC＝6，则△EBC的面积是（ ）
| A．12 | B．9 | C．6 | D． |
9．如图，已知BD是矩形ABCD的对角线，AB＝6，BC＝8，点E，F分别在边AD，BC上，连结BE，DF．将△ABE沿BE翻折，将△DCF沿DF翻折，若翻折后，点A，C分别落在对角线BD上的点G，H处，连结GF．则下列结论不正确 的是（ ）
| A．BD＝10 | B．HG＝2 | C． | D．GF⊥BC |
10．在每个小正方形的边长为1的网格图形中，每个小正方形的顶点称为格点．如图，在6×6的正方形网格图形ABCD中，M，N分别是AB，BC上的格点，BM＝4，BN＝2．若点P是这个网格图形中的格点，连接PM，PN，则所有满足∠MPN＝45°的△PMN中，边PM的长的最大值是（ ）
A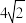． | B．6 | C． | D． |
11．当a＝1时，分式
的值是______ ．
的值是12．“如果
，那么
”的逆命题是___________ ．
，那么”的逆命题是13．如图，已知在△ABC中，D，E分别是AB，AC上的点，
，
．若DE＝2，则BC的长是______ ．
，．若DE＝2，则BC的长是14．一个不透明的箱子里放着分别标有数字1，2，3，4，5，6的六个球，它们除了数字外其余都相同．从这个箱子里随机摸出一个球，摸出的球上所标数字大于4的概率是______ ．
15．如图，已知AB是⊙O的弦，∠AOB＝120°，OC⊥AB，垂足为C，OC的延长线交⊙O于点D．若∠APD是
所对的圆周角，则∠APD的度数是______ ．
所对的圆周角，则∠APD的度数是16．如图，已知在平面直角坐标系xOy中，点A在x轴的负半轴上，点B在y轴的负半轴上，
，以AB为边向上作正方形ABCD．若图像经过点C的反比例函数的解析式是
，则图像经过点D的反比例函数的解析式是______ ．
，以AB为边向上作正方形ABCD．若图像经过点C的反比例函数的解析式是，则图像经过点D的反比例函数的解析式是17．计算：
．
．18．如图，已知在Rt△ABC中，∠C＝90°，AB＝5，BC＝3．求AC的长和sinA的值．
19．解一元一次不等式组
20．为落实“双减”政策，切实减轻学生学业负担，丰富学生课余生活，某校积极开展“五育并举”课外兴趣小组活动，计划成立“爱心传递”、“音乐舞蹈”、“体育运动”、“美工制作”和“劳动体验”五个兴趣小组，要求每位学生都只选其中一个小组．为此，随机抽查了本校各年级部分学生选择兴趣小组的意向，并将抽查结果绘制成如下统计图（不完整）．
根据统计图中的信息，解答下列问题：
(1)求本次被抽查学生的总人数和扇形统计图中表示“美工制作”的扇形的圆心角度数；
(2)将条形统计图补充完整；（温馨提示：请画在答题卷相对应的图上）
(3)该校共有1600名学生，根据抽查结果，试估计全校选择“爱心传递”兴趣小组的学生人数．
根据统计图中的信息，解答下列问题：
(1)求本次被抽查学生的总人数和扇形统计图中表示“美工制作”的扇形的圆心角度数；
(2)将条形统计图补充完整；（温馨提示：请画在答题卷相对应的图上）
(3)该校共有1600名学生，根据抽查结果，试估计全校选择“爱心传递”兴趣小组的学生人数．
21．如图，已知在Rt△ABC中，
，D是AB边上一点，以BD为直径的半圆O与边AC相切，切点为E，过点O作
，垂足为F．
(1)求证：
；
(2)若
，
，求AD的长．
，D是AB边上一点，以BD为直径的半圆O与边AC相切，切点为E，过点O作
，垂足为F．
(1)求证：
；(2)若
，
，求AD的长．22．某校组织学生从学校出发，乘坐大巴前往基地进行研学活动．大巴出发1小时后，学校因事派人乘坐轿车沿相同路线追赶．已知大巴行驶的速度是40千米/小时，轿车行驶的速度是60千米/小时．
(1)求轿车出发后多少小时追上大巴？此时，两车与学校相距多少千米？
(2)如图，图中OB，AB分别表示大巴、轿车离开学校的路程s（千米）与大巴行驶的时间t（小时）的函数关系的图象．试求点B的坐标和AB所在直线的解析式；
(3)假设大巴出发a小时后轿车出发追赶，轿车行驶了1.5小时追上大巴，求a的值．
(1)求轿车出发后多少小时追上大巴？此时，两车与学校相距多少千米？
(2)如图，图中OB，AB分别表示大巴、轿车离开学校的路程s（千米）与大巴行驶的时间t（小时）的函数关系的图象．试求点B的坐标和AB所在直线的解析式；
(3)假设大巴出发a小时后轿车出发追赶，轿车行驶了1.5小时追上大巴，求a的值．
23．如图1，已知在平面直角坐标系xOy中，四边形OABC是边长为3的正方形，其中顶点A，C分别在x轴的正半轴和y轴的正半轴上，抛物线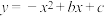
经过A，C两点，与x轴交于另一个点D．
(1)①求点A，B，C的坐标；
②求b，c的值．
(2)若点P是边BC上的一个动点，连结AP，过点P作PM⊥AP，交y轴于点M（如图2所示）．当点P在BC上运动时，点M也随之运动．设BP＝m，CM＝n，试用含m的代数式表示n，并求出n的最大值．
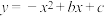经过A，C两点，与x轴交于另一个点D．
(1)①求点A，B，C的坐标；
②求b，c的值．
(2)若点P是边BC上的一个动点，连结AP，过点P作PM⊥AP，交y轴于点M（如图2所示）．当点P在BC上运动时，点M也随之运动．设BP＝m，CM＝n，试用含m的代数式表示n，并求出n的最大值．
24．已知在Rt△ABC中，∠ACB＝90°，a，b分别表示∠A，∠B的对边，
．记△ABC的面积为S．
(1)如图1，分别以AC，CB为边向形外作正方形ACDE和正方形BGFC．记正方形ACDE的面积为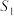
，正方形BGFC的面积为
．
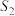①若
，
，求S的值；
②延长EA交GB的延长线于点N，连结FN，交BC于点M，交AB于点H．若FH⊥AB（如图2所示），求证：
．
(2)如图3，分别以AC，CB为边向形外作等边三角形ACD和等边三角形CBE，记等边三角形ACD的面积为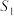，等边三角形CBE的面积为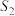．以AB为边向上作等边三角形ABF（点C在△ABF内），连结EF，CF．若EF⊥CF，试探索
与S之间的等量关系，并说明理由．
．记△ABC的面积为S．
(1)如图1，分别以AC，CB为边向形外作正方形ACDE和正方形BGFC．记正方形ACDE的面积为
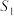，正方形BGFC的面积为
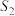．①若
，
，求S的值；②延长EA交GB的延长线于点N，连结FN，交BC于点M，交AB于点H．若FH⊥AB（如图2所示），求证：
．(2)如图3，分别以AC，CB为边向形外作等边三角形ACD和等边三角形CBE，记等边三角形ACD的面积为
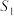，等边三角形CBE的面积为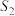．以AB为边向上作等边三角形ABF（点C在△ABF内），连结EF，CF．若EF⊥CF，试探索
与S之间的等量关系，并说明理由．