搜索
．记△ABC的面积为S．
(1)如图1，分别以AC，CB为边向形外作正方形ACDE和正方形BGFC．记正方形ACDE的面积为
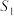，正方形BGFC的面积为
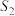．①若
，
，求S的值；②延长EA交GB的延长线于点N，连结FN，交BC于点M，交AB于点H．若FH⊥AB（如图2所示），求证：
．(2)如图3，分别以AC，CB为边向形外作等边三角形ACD和等边三角形CBE，记等边三角形ACD的面积为
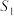，等边三角形CBE的面积为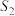．以AB为边向上作等边三角形ABF（点C在△ABF内），连结EF，CF．若EF⊥CF，试探索
与S之间的等量关系，并说明理由．
同类型试题
y = sin x， x∈R， y∈[–1，1]，周期为2π，函数图像以 x = (π/2) + kπ 为对称轴
y = arcsin x， x∈[–1，1]， y∈[–π/2，π/2]
sin x = 0 ←→ arcsin x = 0
sin x = 1/2 ←→ arcsin x = π/6
sin x = √2/2 ←→ arcsin x = π/4
sin x = 1 ←→ arcsin x = π/2
y = sin x， x∈R， y∈[–1，1]，周期为2π，函数图像以 x = (π/2) + kπ 为对称轴
y = arcsin x， x∈[–1，1]， y∈[–π/2，π/2]
sin x = 0 ←→ arcsin x = 0
sin x = 1/2 ←→ arcsin x = π/6
sin x = √2/2 ←→ arcsin x = π/4
sin x = 1 ←→ arcsin x = π/2
