全一卷
1.若等式(x+6)x+1=1成立,那么满足等式成立的x的值的个数有( )
| A.5个 | B.4个 | C.3个 | D.2个 |
2.下列代数式中,属于分式的是( )
| A.5x | B. | C. | D. |
3.某厂准备加工500个零件,在加工了100个零件后,引进了新机器,使每天的工作效率是原来的2倍,结果共用6天完成了任务.若设该厂原来每天加工x个零件,则由题意可列出方程()
A. | B. |
C. | D. |
4.已知 =
= ,
, =
= ,则
,则 的值为( )
的值为( )
 =
= ,
, =
= ,则
,则 的值为( )
的值为( )| A.3 | B.4 | C.6 | D.9 |
5.已知 ,
, ,则
,则 的值为( )
的值为( )
 ,
, ,则
,则 的值为( )
的值为( )| A.6 | B. | C.0 | D.1 |
6.如图,在△ABC和△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,C,D,E三点在同一条直线上,连接BD,则下列结论错误的是( )


| A.△ABD≌△ACE | B.∠ACE+∠DBC=45° |
| C.BD⊥CE | D.∠BAE+∠CAD=200° |
7.如图,在直角三角形ABC中,AC=8,BC=6,∠ACB=90°,点E是AC的中点,点D在AB上,且DE⊥AC于E,则CD=( )


| A.3 | B.4 | C.5 | D.6 |
8.在△ABC中,∠BAC=115°,DE、FG分别为AB、AC的垂直平分线,则∠EAG的度数为( )


| A.50° | B.40° | C.30° | D.25° |
9.如图,已知AB=AC,AD⊥BC,AE=AF,图中共有( )对全等三角形.


| A.5 | B.6 | C.7 | D.8 |
10.如图,在△ABC,∠C=90°,AD平分∠BAC交CB于点D,过点D作DE⊥AB,垂足恰好是边AB的中点E,若AD=3cm,则BE的长为( )


A. cm cm | B.4cm | C.3 cm cm | D.6cm |
11.某广场准备用边长相等的正方形和正三角形两种地砖铺满地面,在每个顶点的周围,正方形和正三角形地砖的块数分别是( )
| A.1、2 | B.2、1 | C.2、2 | D.2、3 |
12.已知实数 ,
, 满足
满足 ,则以
,则以 ,
, 的值为两边长的等腰三角形周长是( )
的值为两边长的等腰三角形周长是( )
 ,
, 满足
满足 ,则以
,则以 ,
, 的值为两边长的等腰三角形周长是( )
的值为两边长的等腰三角形周长是( )| A.20或16 | B.20 | C.16 | D.以上答案均不对 |
13.以下列数据为长度的三条线段,能组成三角形的是( )
| A.2 cm、3cm、5cm | B.2 cm、3 cm、4 cm |
| C.3 cm、5 cm、9 cm | D.8 cm、4 cm、4 cm |
14.将长方形纸片按如图所示的方式折叠,BC、BD为折痕,若∠ABC=35°,则∠DBE的度数为


| A.55° | B.50° | C.45° | D.60° |
15.下列多项式中,能分解因式的是( )
A. | B. | C. | D. |
16.当x______时,分式 有意义.
有意义.
 有意义.
有意义.17.分解因式
___________

18.如图,在 中,
中, ,
, ,
, ,将
,将 绕点
绕点 逆时针旋转
逆时针旋转 得到
得到 ,连接
,连接 ,则
,则 的长为__________.
的长为__________.
 中,
中, ,
, ,
, ,将
,将 绕点
绕点 逆时针旋转
逆时针旋转 得到
得到 ,连接
,连接 ,则
,则 的长为__________.
的长为__________.
19.在△ABC中,∠A=∠B+∠C,∠B=2∠C﹣6°,则∠C的度数为_____ .
20.如图,在 中,
中, ,
, 是
是 的中点,
的中点, ,垂足为
,垂足为 ,
, ,则
,则 的度数是
的度数是______ .

 中,
中, ,
, 是
是 的中点,
的中点, ,垂足为
,垂足为 ,
, ,则
,则 的度数是
的度数是
21.已知 ,
, ,若
,若 ,试求
,试求 的值.
的值.
 ,
, ,若
,若 ,试求
,试求 的值.
的值.22.阅读下面的材料:
我们可以用配方法求一个二次三项式的最大值或最小值,例如:求代数式 的最小值.方法如下:
的最小值.方法如下:
∵ ,由
,由 ,得
,得 ;
;
∴代数式 的最小值是4.
的最小值是4.
(1)仿照上述方法求代数式 的最小值.
的最小值.
(2)代数式 有最大值还是最小值?请用配方法求出这个最值.
有最大值还是最小值?请用配方法求出这个最值.
我们可以用配方法求一个二次三项式的最大值或最小值,例如:求代数式
 的最小值.方法如下:
的最小值.方法如下:∵
 ,由
,由 ,得
,得 ;
;∴代数式
 的最小值是4.
的最小值是4.(1)仿照上述方法求代数式
 的最小值.
的最小值.(2)代数式
 有最大值还是最小值?请用配方法求出这个最值.
有最大值还是最小值?请用配方法求出这个最值.23.如图,A(0,4)是直角坐标系y轴上一点,动点P从原点O出发,沿x轴正半轴运动,速度为每秒1个单位长度,以P为直角顶点在第一象限内作等腰Rt△APB.设P点的运动时间为t秒.

(1)若AB//x轴,求t的值;
(2)当t=3时,坐标平面内有一点M(不与A重合),使得以M、P、B为顶点的三角形和△ABP全等,请求出点M的坐标;

(1)若AB//x轴,求t的值;
(2)当t=3时,坐标平面内有一点M(不与A重合),使得以M、P、B为顶点的三角形和△ABP全等,请求出点M的坐标;
24.如图,点 是等边
是等边 内一点,
内一点, ,
, ,将
,将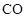 绕点
绕点 顺时针方向旋转
顺时针方向旋转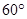 得到
得到 ,连接
,连接 ,
, .
.

(1)当 时,判断
时,判断 的形状,并说明理由;
的形状,并说明理由;
(2)求 的度数;
的度数;
(3)请你探究:当 为多少度时,
为多少度时, 是等腰三角形?
是等腰三角形?
 是等边
是等边 内一点,
内一点, ,
, ,将
,将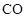 绕点
绕点 顺时针方向旋转
顺时针方向旋转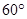 得到
得到 ,连接
,连接 ,
, .
.
(1)当
 时,判断
时,判断 的形状,并说明理由;
的形状,并说明理由;(2)求
 的度数;
的度数;(3)请你探究:当
 为多少度时,
为多少度时, 是等腰三角形?
是等腰三角形?25.如图,AB∥EF,AD平分∠BAC,且∠C=45°,∠CDE=125°,求∠ADF的度数.

 搜索
搜索
 难度系数:0.65
难度系数:0.65  答案解析
答案解析
 有奖纠错
有奖纠错
