全一卷
1.-8的绝对值是【 】
| A.8 | B. | C.- | D.-8 |
2.形状相同、大小相等的两个小木块放置于桌面,其俯视图如下图所示,则其主视图是( )


A. | B. | C. | D. |
3.如图,已知BE平分∠ABC,且BE∥DC,若∠ABC=50°,则∠C的度数是( )


| A.20° | B.25° | C.30° | D.50° |
4.已知 ,则正比例函数
,则正比例函数 的图象经过( )
的图象经过( )
 ,则正比例函数
,则正比例函数 的图象经过( )
的图象经过( )| A.第二、四象限, | B.第二、三象限 | C.第一、三象限 | D.第一、四象限 |
5.下列运算正确的是( )
A. | B. |
C. | D. |
6.如图, 经过
经过 的重心,点
的重心,点 是
是 的中点,过点
的中点,过点 作
作 交
交 于点
于点 ,若
,若 ,则线段
,则线段 的长为( )
的长为( )

 经过
经过 的重心,点
的重心,点 是
是 的中点,过点
的中点,过点 作
作 交
交 于点
于点 ,若
,若 ,则线段
,则线段 的长为( )
的长为( )
| A.6 | B.4 | C.5 | D.3 |
7.若三点 在同一直线上,则
在同一直线上,则 的值等于( )
的值等于( )
 在同一直线上,则
在同一直线上,则 的值等于( )
的值等于( )| A.5 | B.6 | C.-1 | D.4 |
8.如图,在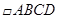 中,
中, 的平分线交
的平分线交 于点
于点 ,交
,交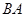 的延长线于点
的延长线于点 ,则
,则 的长为( )
的长为( )

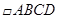 中,
中, 的平分线交
的平分线交 于点
于点 ,交
,交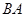 的延长线于点
的延长线于点 ,则
,则 的长为( )
的长为( )
| A.4 | B.2 | C.3 | D.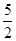 |
9.已知AB是⊙O半径OC的垂直平分线,点P是劣弧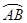 上的点,则
上的点,则 的度数为( )
的度数为( )
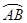 上的点,则
上的点,则 的度数为( )
的度数为( )A. | B. | C. | D. |
10.已知二次函数y=ax2+2ax+3a2+3(其中x是自变量),当x≥2时,y随x的增大而增大,且-2≤x≤1时,y的最大值为9,则a的值为



A.1或 | B.- 或 或 | C. | D.1 |
11.因式分解:m2n+2mn2+n3=_____.
12.如图,已知正六边形 ,连接
,连接 ,则
,则 _________°.
_________°.
 ,连接
,连接 ,则
,则 _________°.
_________°.
13.如图,在平面直角坐标系中,点A在第二象限内,点B在x轴上,∠AOB=30°,AB=BO,反比例函数y= (x<0)的图象经过点A,若S△AOB=
(x<0)的图象经过点A,若S△AOB= ,则k的值为
,则k的值为________ .

 (x<0)的图象经过点A,若S△AOB=
(x<0)的图象经过点A,若S△AOB= ,则k的值为
,则k的值为
14.如图,在 中,
中, ,
, ,
, ,点F在边AC上,点E为边BC上的动点,将
,点F在边AC上,点E为边BC上的动点,将 沿直线EF翻折,点C落在点P处.若
沿直线EF翻折,点C落在点P处.若 ,则点P到AB距离的最小值为
,则点P到AB距离的最小值为________ .
 中,
中, ,
, ,
, ,点F在边AC上,点E为边BC上的动点,将
,点F在边AC上,点E为边BC上的动点,将 沿直线EF翻折,点C落在点P处.若
沿直线EF翻折,点C落在点P处.若 ,则点P到AB距离的最小值为
,则点P到AB距离的最小值为
15.计算:

16.化简:(

17.如图,已知 中,
中, ,点
,点 在边
在边 上,请利用尺规作图法在
上,请利用尺规作图法在 边上求作点
边上求作点 ,使
,使 .(不写作法,保留作图痕迹)
.(不写作法,保留作图痕迹)

 中,
中, ,点
,点 在边
在边 上,请利用尺规作图法在
上,请利用尺规作图法在 边上求作点
边上求作点 ,使
,使 .(不写作法,保留作图痕迹)
.(不写作法,保留作图痕迹)
18.如图,AB∥CD,E是CD上一点,BE交AD于点F,EF=BF.求证:AF=DF.


19.现代人对于健康越来越重视,比起去健身房或者运动量较大的户外活动,不少人更钟爱健步走.如今,在朋友圈里晒步数拼排行抢封面是不少人健步走的乐趣所在,“日行万步”已经成为众多运动爱好者的标配,在一次社会调查活动中,小李随机抽取某“健步走运动”团队20名成员,收集他们一天行走的步数,记录如下:
对这20个数据按组距1000进行分组,并统计整理,绘制了如下不完整的统计图表.

根据以上信息解答下列问题:
(1)补全两幅统计图;
(2)这20名“健步走运动”团队成员一天行走的步数的中位数落在 组;其中D组.数据的平均数 步;
(3)若该团队共有200人,请估计其中一天行走步数少于8500步的人数.
| 5640 | 6430 | 6520 | 6798 | 7325 |
| 8430 | 8215 | 7453 | 7446 | 6754 |
| 7638 | 6834 | 7326 | 6830 | 8648 |
| 8752 | 9450 | 9865 | 7290 | 7850 |
对这20个数据按组距1000进行分组,并统计整理,绘制了如下不完整的统计图表.
| 组别 | 步数分组 |
| A |  |
| B |  |
| C |  |
| D |  |
| E |  |

根据以上信息解答下列问题:
(1)补全两幅统计图;
(2)这20名“健步走运动”团队成员一天行走的步数的中位数落在 组;其中D组.数据的平均数 步;
(3)若该团队共有200人,请估计其中一天行走步数少于8500步的人数.
20.长安塔,又名天人长安塔,位于西安世园会园区制高点小终南山上,是西安世园会的标志,也是园区的观景塔,游人可登塔俯瞰,全园美景尽收眼底。小军利用刚学过的测量知识来测量长安塔的高度,如图所示,他和学习小组的同学带着测量工具来到长安塔前,恰好发现有一个临时搭建的台子 ,小军在台子底部
,小军在台子底部 处测得塔顶
处测得塔顶 的仰角为
的仰角为 ,然后又到台子的顶端
,然后又到台子的顶端 处测得塔顶
处测得塔顶 的仰角为
的仰角为 ,已知
,已知 均垂直于
均垂直于 ,求长安塔的高度
,求长安塔的高度 .(参考数据
.(参考数据 ,
, )
)
 ,小军在台子底部
,小军在台子底部 处测得塔顶
处测得塔顶 的仰角为
的仰角为 ,然后又到台子的顶端
,然后又到台子的顶端 处测得塔顶
处测得塔顶 的仰角为
的仰角为 ,已知
,已知 均垂直于
均垂直于 ,求长安塔的高度
,求长安塔的高度 .(参考数据
.(参考数据 ,
, )
)
21.在全球关注的抗击“新冠肺炎”中某跨国科研中心的一个团队研制了一种助治“新冠附炎”的新药,在试验药效时发现,如果成人按规定的制量服用,那么服药后2小时血液中含药量最高,达每毫升8微克(1微克= 毫克),接着逐步安减,10小时时血液中含药最为每毫升3微克,每毫升血液中含药量
毫克),接着逐步安减,10小时时血液中含药最为每毫升3微克,每毫升血液中含药量 (微克)随时间
(微克)随时间 (小时)的变化如图所示.
(小时)的变化如图所示.

(1)分别求线段 所表示的函数关系式;
所表示的函数关系式;
(2)如果每毫升血液中含药量为4微克或4微克以上时对治病是有效的,那么这个有效时间是多长?
 毫克),接着逐步安减,10小时时血液中含药最为每毫升3微克,每毫升血液中含药量
毫克),接着逐步安减,10小时时血液中含药最为每毫升3微克,每毫升血液中含药量 (微克)随时间
(微克)随时间 (小时)的变化如图所示.
(小时)的变化如图所示.
(1)分别求线段
 所表示的函数关系式;
所表示的函数关系式;(2)如果每毫升血液中含药量为4微克或4微克以上时对治病是有效的,那么这个有效时间是多长?
22.2022年北京冬奥会吉祥物“冰墩墩”以熊猫为原型进行设计创作,北京冬残奥会吉祥物“雪容融”则以中国标志性符号的灯笼为创意进行设计创作“冰墩墩”和“雪容融”是一个非常完美的搭:配和组合,是中国文化和奥林匹克精神又一次完美的结合莉莉有“冰墩墩”和“雪容融”的纪念邮票各2张(如图),这4张邮票背面完全相同,莉莉想给好友小婷和小华各送一张纪念邮票,她先让小婷从这4张邮票中随机抽取一张,然后,再让小华从剩下的3张中随机抽取一张.

(1)小婷抽到“冰墩墩”的纪念邮票的概率是__________.
(2)利用树状图或列表法求小婷和小华均抽到“雪容融”的纪念邮票的概率.

(1)小婷抽到“冰墩墩”的纪念邮票的概率是__________.
(2)利用树状图或列表法求小婷和小华均抽到“雪容融”的纪念邮票的概率.
23.如图, 与
与 的斜边
的斜边 相切于点
相切于点 ,与直角边
,与直角边 相交于
相交于 两点,连接
两点,连接 ,
, .
.

(1)求证: ;
;
(2)若 ,
, ,
,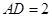 ,求线段
,求线段 的长度.
的长度.
 与
与 的斜边
的斜边 相切于点
相切于点 ,与直角边
,与直角边 相交于
相交于 两点,连接
两点,连接 ,
, .
.
(1)求证:
 ;
;(2)若
 ,
, ,
,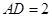 ,求线段
,求线段 的长度.
的长度.24.如图,抛物线 交
交 轴于
轴于 ,交
,交 轴于
轴于 ,直线
,直线 平行于
平行于 轴,与抛物线另一个交点为
轴,与抛物线另一个交点为 .
.

(1)求抛物线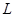 的函数表达式及点D的坐标;
的函数表达式及点D的坐标;
(2)若抛物线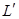 与抛物线
与抛物线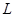 关于
关于 轴对称,
轴对称, 是
是 轴上的动点,在抛物线
轴上的动点,在抛物线 上是否存在一点
上是否存在一点 ,使得以
,使得以 为顶点且
为顶点且 为边的四边形是平行四边形,若存在,请求出点
为边的四边形是平行四边形,若存在,请求出点 的坐标,若不存在,请说明理由.
的坐标,若不存在,请说明理由.
 交
交 轴于
轴于 ,交
,交 轴于
轴于 ,直线
,直线 平行于
平行于 轴,与抛物线另一个交点为
轴,与抛物线另一个交点为 .
.
(1)求抛物线
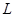 的函数表达式及点D的坐标;
的函数表达式及点D的坐标;(2)若抛物线
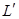 与抛物线
与抛物线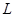 关于
关于 轴对称,
轴对称, 是
是 轴上的动点,在抛物线
轴上的动点,在抛物线 上是否存在一点
上是否存在一点 ,使得以
,使得以 为顶点且
为顶点且 为边的四边形是平行四边形,若存在,请求出点
为边的四边形是平行四边形,若存在,请求出点 的坐标,若不存在,请说明理由.
的坐标,若不存在,请说明理由.25.问题提出
(1)如图, 是
是 的弦,点
的弦,点 是
是 上的一点,在直线
上的一点,在直线 上方找一点
上方找一点 ,使得
,使得 ,画出
,画出 ,并说明理由;
,并说明理由;

问题探究
(2)如图, 是
是 的弦,直线
的弦,直线 与
与 相切于点
相切于点 ,点
,点 ,是直线
,是直线 上异于点
上异于点 的任意一点,请在图中画出图形,试判断
的任意一点,请在图中画出图形,试判断 的大小关系;并说明理由;
的大小关系;并说明理由;

问题解决
(3)如图,有一个平面图为五边形ABCDE的展览馆,其中 ,
, ,
, .展览馆保卫人员想在线段
.展览馆保卫人员想在线段 上选一点
上选一点 安装监控装置,用来监视边
安装监控装置,用来监视边 ,现只要使
,现只要使 最大,就可以让监控装置的效果达到最佳,问在线段
最大,就可以让监控装置的效果达到最佳,问在线段 上是否存在点
上是否存在点 ,使
,使 最大?若存在,请求出符合条件的
最大?若存在,请求出符合条件的 的长,若不存在,请说明理由.
的长,若不存在,请说明理由.

(1)如图,
 是
是 的弦,点
的弦,点 是
是 上的一点,在直线
上的一点,在直线 上方找一点
上方找一点 ,使得
,使得 ,画出
,画出 ,并说明理由;
,并说明理由;
问题探究
(2)如图,
 是
是 的弦,直线
的弦,直线 与
与 相切于点
相切于点 ,点
,点 ,是直线
,是直线 上异于点
上异于点 的任意一点,请在图中画出图形,试判断
的任意一点,请在图中画出图形,试判断 的大小关系;并说明理由;
的大小关系;并说明理由;
问题解决
(3)如图,有一个平面图为五边形ABCDE的展览馆,其中
 ,
, ,
, .展览馆保卫人员想在线段
.展览馆保卫人员想在线段 上选一点
上选一点 安装监控装置,用来监视边
安装监控装置,用来监视边 ,现只要使
,现只要使 最大,就可以让监控装置的效果达到最佳,问在线段
最大,就可以让监控装置的效果达到最佳,问在线段 上是否存在点
上是否存在点 ,使
,使 最大?若存在,请求出符合条件的
最大?若存在,请求出符合条件的 的长,若不存在,请说明理由.
的长,若不存在,请说明理由.
 搜索
搜索
 难度系数:0.94
难度系数:0.94  答案解析
答案解析
 有奖纠错
有奖纠错
