搜索
全一卷
难度系数：0.85 
答案解析
有奖纠错
1．李师傅做了一个零件，如图，请你告诉他这个零件的主视图是（ ）
A． | B． | C． | D． |
2．小张用手机拍摄得到甲图，经放大后得到乙图，甲图中的线段AB在乙图中的对应线段是（ ）
| A．FG | B．FH | C．EH | D．EF |
3．如图，直线
与直线
相交于点
，
的度数是（ ）
与直线相交于点，的度数是（ ） A． | B． | C． | D． |
4．如图，小强利用全等三角形的知识测量池塘两端M、N的距离，如果△PQO≌△NMO，则只需测出其长度的线段是（ ）
| A．PO | B．PQ | C．MO | D．MQ |
5．娜娜有一个问题请教你，下列图形中对称轴只有两条的是（）
6．如图，给出了正方形ABCD的面积的四个表达式，其中错误的是（ ）
| A．（x+a）（x+a） | B．x2+a2+2ax | C．（x-a）（x-a） | D．（x+a）a+（x+a）x |
7．定圆O的半径是4cm，动圆P的半径是2cm，动圆在直线l上移动，当两圆相切时，OP的值是（ ）
| A．2cm或6cm | B．2cm | C．4cm | D．6cm |
8．你认为方程x2+2x-3=0的解应该是（）
| A．1 | B．-3 | C．3 | D．1或-3 |
9．如图，P1、P2、P3这三个点中，在第二象限内的有（）
| A．P1、P2、P3 | B．P1、P2 | C．P1、P3 | D．P1 |
10．如图，小红做了一个实验，将正六边形ABCDEF绕点F顺时针旋转后到达A′B′C′D′E′F′的位置，所转过的度数是（）
| A．60° | B．72° | C．108° | D．120° |
11．小芳给你一个如图所示的量角器，如果你用它来度量角的度数，那么能精确地读出的最小度数是（）
| A．1° | B．5° | C．10° | D．180° |
12．小兰画了一个函数
的图象如图，那么关于x的分式方程
的解是（ ）
的图象如图，那么关于x的分式方程
的解是（ ）
| A．x=1 | B．x=2 | C．x=3 | D．x=4 |
13．如图，在△ABC中，BD是∠ABC的角平分线，已知∠ABC=80°，则∠DBC= ．
14．如图，x和5分别是天平上两边的砝码，请你用大于号“＞”或小于号“＜”填空：x________ 5．
15．一元二次方程3x2+2x-5=0的一次项系数是_____ ．
16．一个圆锥形的漏斗，小李用三角板测得其高度的尺寸如图所示，那么漏斗的斜壁AB的长度为cm．
17．某校篮球队在一次定点投篮训练中进球情况如图，那么这个对的队员平均进球个数是 ．
18．已知：在△ABC中，AC=a，AB与BC所在直线成45°角，AC与BC所在直线形成的夹角的余弦值为
（即cosC=），则AC边上的中线长是_____________ ．
（即cosC=），则AC边上的中线长是19．计算：
20．列方程解应用题：
今年“六•一”儿童节，张红用8.8元钱购买了甲、乙两种礼物，甲礼物每件1.2元，乙礼物每件0.8元，其中甲礼物比乙礼物少1件，问甲、乙两种礼物各买了多少件？
今年“六•一”儿童节，张红用8.8元钱购买了甲、乙两种礼物，甲礼物每件1.2元，乙礼物每件0.8元，其中甲礼物比乙礼物少1件，问甲、乙两种礼物各买了多少件？
21．右表反映了x与y之间存在某种函数关系，现给出了几种可能的函数关系式：
y=x+7，y=x-5，
，
（1）从所给出的几个式子中选出一个你认为满足上表要求的函数表达式： ；
（2）请说明你选择这个函数表达式的理由．
y=x+7，y=x-5，
，
| x | … | -6 | -5 | 3 | 4 | … |
| y | … | 1 | 1.2 | -2 | -1.5 | … |
（1）从所给出的几个式子中选出一个你认为满足上表要求的函数表达式： ；
（2）请说明你选择这个函数表达式的理由．
22．在甲、乙两个袋子中分别装有如图点数的牌，假设随机从袋子中抽牌时，每张牌被抽到的机会是均等的．那么分别从两个袋子各抽取1张牌时，它们的点数之和大于10的概率是多少？
23．如图，用两张等宽的纸条交叉重叠地放在一起，重合的四边形ABCD是一个特殊的四边形．
（1）这个特殊的四边形应该叫做 .
（2）请证明你的结论．
（1）这个特殊的四边形应该叫做 .
（2）请证明你的结论．
24．已知：抛物线
．
（1）写出抛物线的开口方向、对称轴；
（2）函数y有最大值还是最小值？并求出这个最大（小）值；
（3）设抛物线与y轴的交点为P，与x轴的交点为Q，求直线PQ的函数解析式．
．（1）写出抛物线的开口方向、对称轴；
（2）函数y有最大值还是最小值？并求出这个最大（小）值；
（3）设抛物线与y轴的交点为P，与x轴的交点为Q，求直线PQ的函数解析式．
25．如图，AB是⊙O的直径，AC是弦．
（1）请你按下面步骤画图（画图或作辅助线时先使用铅笔画出，确定后必须使用黑色字迹的签字笔描黑）；
第一步，过点A作∠BAC的角平分线，交⊙O于点D；
第二步，过点D作AC的垂线，交AC的延长线于点E．
第三步，连接BD．
（2）求证：AD2=AE•AB；
（3）连接EO，交AD于点F，若5AC=3AB，求
的值．
（1）请你按下面步骤画图（画图或作辅助线时先使用铅笔画出，确定后必须使用黑色字迹的签字笔描黑）；
第一步，过点A作∠BAC的角平分线，交⊙O于点D；
第二步，过点D作AC的垂线，交AC的延长线于点E．
第三步，连接BD．
（2）求证：AD2=AE•AB；
（3）连接EO，交AD于点F，若5AC=3AB，求
的值．26．如图，在△ABC中，AB=2，AC=BC=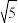
．
（1）以AB所在的直线为x轴，AB的垂直平分线为y轴，建立直角坐标系如图，请你分别写出A、B、C三点的坐标；
（2）求过A、B、C三点且以C为顶点的抛物线的解析式；
（3）若D为抛物线上的一动点，当D点坐标为何值时，S△ABD=
S△ABC；
（4）如果将（2）中的抛物线向右平移，且与x轴交于点A′、B′，与y轴交于点C′，当平移多少个单位时，点C′同时在以A′B′为直径的圆上（解答过程如果有需要时，请参看阅读材料）．
附：阅读材料
一元二次方程常用的解法有配方法、公式法和因式分解法，对于一些特殊方程可以通过换元法转化为一元二次方程求解．如解方程：y4-4y2+3=0．
解：令y2=x（x≥0），则原方程变为x2-4x+3=0，解得x1=1，x2=3．
当x1=1时，即y2=1，
∴y1=1，y2=-1．
当x2=3，即y2=3，
∴y3=3 ，y4=-3．
所以，原方程的解是y1=1，y2=-1，y3= 3，y4=- 3．
再如
，可设
，用同样的方法也可求解．
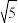．（1）以AB所在的直线为x轴，AB的垂直平分线为y轴，建立直角坐标系如图，请你分别写出A、B、C三点的坐标；
（2）求过A、B、C三点且以C为顶点的抛物线的解析式；
（3）若D为抛物线上的一动点，当D点坐标为何值时，S△ABD=
S△ABC；（4）如果将（2）中的抛物线向右平移，且与x轴交于点A′、B′，与y轴交于点C′，当平移多少个单位时，点C′同时在以A′B′为直径的圆上（解答过程如果有需要时，请参看阅读材料）．
附：阅读材料
一元二次方程常用的解法有配方法、公式法和因式分解法，对于一些特殊方程可以通过换元法转化为一元二次方程求解．如解方程：y4-4y2+3=0．
解：令y2=x（x≥0），则原方程变为x2-4x+3=0，解得x1=1，x2=3．
当x1=1时，即y2=1，
∴y1=1，y2=-1．
当x2=3，即y2=3，
∴y3=3 ，y4=-3．
所以，原方程的解是y1=1，y2=-1，y3= 3，y4=- 3．
再如
，可设
，用同样的方法也可求解．