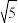搜索
．（1）以AB所在的直线为x轴，AB的垂直平分线为y轴，建立直角坐标系如图，请你分别写出A、B、C三点的坐标；
（2）求过A、B、C三点且以C为顶点的抛物线的解析式；
（3）若D为抛物线上的一动点，当D点坐标为何值时，S△ABD=
S△ABC；（4）如果将（2）中的抛物线向右平移，且与x轴交于点A′、B′，与y轴交于点C′，当平移多少个单位时，点C′同时在以A′B′为直径的圆上（解答过程如果有需要时，请参看阅读材料）．
附：阅读材料
一元二次方程常用的解法有配方法、公式法和因式分解法，对于一些特殊方程可以通过换元法转化为一元二次方程求解．如解方程：y4-4y2+3=0．
解：令y2=x（x≥0），则原方程变为x2-4x+3=0，解得x1=1，x2=3．
当x1=1时，即y2=1，
∴y1=1，y2=-1．
当x2=3，即y2=3，
∴y3=3 ，y4=-3．
所以，原方程的解是y1=1，y2=-1，y3= 3，y4=- 3．
再如
，可设
，用同样的方法也可求解．
同类型试题
y = sin x， x∈R， y∈[–1，1]，周期为2π，函数图像以 x = (π/2) + kπ 为对称轴
y = arcsin x， x∈[–1，1]， y∈[–π/2，π/2]
sin x = 0 ←→ arcsin x = 0
sin x = 1/2 ←→ arcsin x = π/6
sin x = √2/2 ←→ arcsin x = π/4
sin x = 1 ←→ arcsin x = π/2
y = sin x， x∈R， y∈[–1，1]，周期为2π，函数图像以 x = (π/2) + kπ 为对称轴
y = arcsin x， x∈[–1，1]， y∈[–π/2，π/2]
sin x = 0 ←→ arcsin x = 0
sin x = 1/2 ←→ arcsin x = π/6
sin x = √2/2 ←→ arcsin x = π/4
sin x = 1 ←→ arcsin x = π/2
