全一卷
1.-2019的相反数是( )
| A.2019 | B.-2019 | C. | D. |
2.中国陆地面积约为 ,将数字9600000用科学记数法表示为()
,将数字9600000用科学记数法表示为()
 ,将数字9600000用科学记数法表示为()
,将数字9600000用科学记数法表示为()A. | B. | C. | D. |
3.如图,立体图形的俯视图是( )


A. | B. | C. | D. |
4.下列运算中,计算正确的是()
A. | B. |
C. | D. |
5.在平面直角坐标系中,点 关于原点对称点在()
关于原点对称点在()
 关于原点对称点在()
关于原点对称点在()| A.第一象限 | B.第二象限 | C.第三象限 | D.第四象限 |
6.如图,三角板的直角顶点落在矩形纸片的一边上.若∠1=35°,则∠2的度数是( )


| A.35° | B.45° | C.55° | D.65° |
7.如图,点B、F、C、E在一条直线上,AB∥ED,AC∥FD,那么添加下列一个条件后,仍无法判定△ABC≌△DEF的是( )


| A.AB=DE | B.AC=DF | C.∠A=∠D | D.BF=EC |
8.如图,半径为3的⊙A经过原点O和点C(0,2),B是y轴左侧⊙A优弧上一点,则tan∠OBC为( )


A. | B.2 | C. | D. |
9.如图,在菱形ABCD中,按以下步骤作图:①分别以点C和点D为圆心,大于 为半径作弧,两弧交于点M,N;②作直线MN,且
为半径作弧,两弧交于点M,N;②作直线MN,且 恰好经过点A,与CD交于点E,连接BE,则下列说法错误的是( )
恰好经过点A,与CD交于点E,连接BE,则下列说法错误的是( )

 为半径作弧,两弧交于点M,N;②作直线MN,且
为半径作弧,两弧交于点M,N;②作直线MN,且 恰好经过点A,与CD交于点E,连接BE,则下列说法错误的是( )
恰好经过点A,与CD交于点E,连接BE,则下列说法错误的是( )
A. | B. | C.若AB=4,则 | D. |
10.如图,已知二次函数 的图象与
的图象与 轴分别交于
轴分别交于 、
、 两点,与
两点,与 轴交于
轴交于 点,
点, .则由抛物线的特征写出如下结论:①
.则由抛物线的特征写出如下结论:① ;②
;② ;③
;③ ;④
;④ .其中正确的个数是()
.其中正确的个数是()

 的图象与
的图象与 轴分别交于
轴分别交于 、
、 两点,与
两点,与 轴交于
轴交于 点,
点, .则由抛物线的特征写出如下结论:①
.则由抛物线的特征写出如下结论:① ;②
;② ;③
;③ ;④
;④ .其中正确的个数是()
.其中正确的个数是()
| A.4个 | B.3个 | C.2个 | D.1个 |
11.函数 中,自变量
中,自变量 的取值范围是
的取值范围是_____ .
 中,自变量
中,自变量 的取值范围是
的取值范围是12.若实数 、
、 满足
满足 ,则
,则
________ .
 、
、 满足
满足 ,则
,则
13.如图,沿一条母线将圆锥侧面剪开并展平,得到一个扇形,若圆锥的底面圆的半径 ,扇形的圆心角
,扇形的圆心角 ,则该圆锥的母线长
,则该圆锥的母线长 为
为___  .
.

 ,扇形的圆心角
,扇形的圆心角 ,则该圆锥的母线长
,则该圆锥的母线长 为
为 .
.
14.某生态示范园计划种植一批蜂糖李,原计划总产量达36万千克,为了满足市场需求,现决定改良蜂糖李品种,改良后平均每亩产量是原计划的1.5倍,总产量比原计划增加了9万千克,种植亩数减少了20亩,则原计划和改良后平均每亩产量各多少万千克?设原计划平均亩产量为 万千克,则改良后平均每亩产量为
万千克,则改良后平均每亩产量为 万千克,根据题意列方程为
万千克,根据题意列方程为________ .
 万千克,则改良后平均每亩产量为
万千克,则改良后平均每亩产量为 万千克,根据题意列方程为
万千克,根据题意列方程为15.如图,直线 轴于点
轴于点 ,且与反比例函数
,且与反比例函数 (
( )及
)及 (
( )的图象分别交于
)的图象分别交于 、
、 两点,连接
两点,连接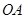 、
、 ,已知
,已知 的面积为4,则
的面积为4,则 ________.
________.
 轴于点
轴于点 ,且与反比例函数
,且与反比例函数 (
( )及
)及 (
( )的图象分别交于
)的图象分别交于 、
、 两点,连接
两点,连接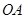 、
、 ,已知
,已知 的面积为4,则
的面积为4,则 ________.
________.
16.已知一组数据 的方差为2,则另一组数据
的方差为2,则另一组数据 的方差为________.
的方差为________.
 的方差为2,则另一组数据
的方差为2,则另一组数据 的方差为________.
的方差为________.17.如图,在 中,
中, ,且
,且 ,
, ,点
,点 是斜边
是斜边 上的一个动点,过点
上的一个动点,过点 分别作
分别作 于点
于点 ,
, 于点
于点 ,连接
,连接 ,则线段
,则线段 的最小值为
的最小值为________ .

 中,
中, ,且
,且 ,
, ,点
,点 是斜边
是斜边 上的一个动点,过点
上的一个动点,过点 分别作
分别作 于点
于点 ,
, 于点
于点 ,连接
,连接 ,则线段
,则线段 的最小值为
的最小值为
18.将从1开始的自然数按以下规律排列,例如位于第3行、第4列的数是12,则位于第45行、第8列的数是__________ .


19.计算: .
.
 .
.20.先化简 ,再从不等式组
,再从不等式组 的整数解中选一个合适的
的整数解中选一个合适的 的值代入求值.
的值代入求值.
 ,再从不等式组
,再从不等式组 的整数解中选一个合适的
的整数解中选一个合适的 的值代入求值.
的值代入求值.21.安顺市某商贸公司以每千克40元的价格购进一种干果,计划以每千克60元的价格销售,为了让顾客得到更大的实惠,现决定降价销售,已知这种干果销售量 (千克)与每千克降价
(千克)与每千克降价 (元)
(元) 之间满足一次函数关系,其图象如图所示:
之间满足一次函数关系,其图象如图所示:

(1)求 与
与 之间的函数关系式;
之间的函数关系式;
(2)商贸公司要想获利2090元,则这种干果每千克应降价多少元?
 (千克)与每千克降价
(千克)与每千克降价 (元)
(元) 之间满足一次函数关系,其图象如图所示:
之间满足一次函数关系,其图象如图所示:
(1)求
 与
与 之间的函数关系式;
之间的函数关系式;(2)商贸公司要想获利2090元,则这种干果每千克应降价多少元?
22.阅读以下材料:
对数的创始人是苏格兰数学家纳皮尔(J.Nplcr,1550﹣1617年),纳皮尔发明对数是在指数书写方式之前,直到18世纪瑞士数学家欧拉(Evlcr,1707﹣1783年)才发现指数与对数之间的联系.
对数的定义:一般地,若 (
( 且
且 ),那么
),那么 叫做以
叫做以 为底
为底 的对数,记作
的对数,记作 ,比如指数式
,比如指数式 可以转化为对数式
可以转化为对数式 ,对数式
,对数式 ,可以转化为指数式
,可以转化为指数式 .
.
我们根据对数的定义可得到对数的一个性质:
 (
( ,
,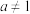 ,
, ,
, ),理由如下:
),理由如下:
设 ,
, ,则
,则 ,
, ,
,
∴ ,由对数的定义得
,由对数的定义得
又∵
∴
根据阅读材料,解决以下问题:
(1)将指数式 转化为对数式________;
转化为对数式________;
(2)求证: (
( ,
,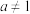 ,
, ,
, )
)
(3)拓展运用:计算 ________.
________.
对数的创始人是苏格兰数学家纳皮尔(J.Nplcr,1550﹣1617年),纳皮尔发明对数是在指数书写方式之前,直到18世纪瑞士数学家欧拉(Evlcr,1707﹣1783年)才发现指数与对数之间的联系.
对数的定义:一般地,若
 (
( 且
且 ),那么
),那么 叫做以
叫做以 为底
为底 的对数,记作
的对数,记作 ,比如指数式
,比如指数式 可以转化为对数式
可以转化为对数式 ,对数式
,对数式 ,可以转化为指数式
,可以转化为指数式 .
.我们根据对数的定义可得到对数的一个性质:
 (
( ,
,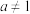 ,
, ,
, ),理由如下:
),理由如下:设
 ,
, ,则
,则 ,
, ,
,∴
 ,由对数的定义得
,由对数的定义得
又∵

∴

根据阅读材料,解决以下问题:
(1)将指数式
 转化为对数式________;
转化为对数式________;(2)求证:
 (
( ,
,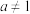 ,
, ,
, )
)(3)拓展运用:计算
 ________.
________.23.近年来,在习近平总书记“既要金山银山,又要绿水青山”思想的指导下,我国持续的大面积雾霾天气得到了较大改善.为了调查学生对雾霾天气知识的了解程度,某校在学生中做了一次抽样调查,调查结果共分为四个等级:A.非常了解;B.比较了解;C.基本了解;D.不了解.根据调查统计结果,绘制了如图所示的不完整的三种统计图表.

对雾霾天气了解程度的统计表
请结合统计图表,回答下列问题:
(1)本次参与调查的学生共有________, ________;
________;
(2)扇形统计图中 部分扇形所对应的圆心角是________度;
部分扇形所对应的圆心角是________度;
(3)请补全条形统计图;
(4)根据调查结果,学校准备开展关于雾霾的知识竞赛,某班要从“非常了解”程度的小明和小刚中选一人参加,现设计了如下游戏来确定,具体规则是:把四个完全相同的乒乓球分别标上数字1,2,3,4,然后放到一个不透明的袋中充分摇匀,一个人先从袋中随机摸出一个球,另一人再从剩下的三个球中随机摸出一个球.若摸出的两个球上的数字和为奇数,则小明去,否则小刚去.请用树状图或列表法说明这个游戏规则是否公平.

对雾霾天气了解程度的统计表
| 对雾霾天气了解程度 | 百分比 |
| A.非常了解 |  |
| B.比较了解 |  |
| C.基本了解 |  |
| D.不了解 |  |
请结合统计图表,回答下列问题:
(1)本次参与调查的学生共有________,
 ________;
________;(2)扇形统计图中
 部分扇形所对应的圆心角是________度;
部分扇形所对应的圆心角是________度;(3)请补全条形统计图;
(4)根据调查结果,学校准备开展关于雾霾的知识竞赛,某班要从“非常了解”程度的小明和小刚中选一人参加,现设计了如下游戏来确定,具体规则是:把四个完全相同的乒乓球分别标上数字1,2,3,4,然后放到一个不透明的袋中充分摇匀,一个人先从袋中随机摸出一个球,另一人再从剩下的三个球中随机摸出一个球.若摸出的两个球上的数字和为奇数,则小明去,否则小刚去.请用树状图或列表法说明这个游戏规则是否公平.
24.(1)如图①,在四边形 中,
中, ,点
,点 是
是 的中点,若
的中点,若 是
是 的平分线,试判断
的平分线,试判断 ,
, ,
, 之间的等量关系.
之间的等量关系.
解决此问题可以用如下方法:延长 交
交 的延长线于点
的延长线于点 ,易证
,易证 得到
得到 ,从而把
,从而把 ,
, ,
, 转化在一个三角形中即可判断.
转化在一个三角形中即可判断.
 ,
, ,
, 之间的等量关系________;
之间的等量关系________;
(2)问题探究:如图②,在四边形 中,
中, ,
, 与
与 的延长线交于点
的延长线交于点 ,点
,点 是
是 的中点,若
的中点,若 是
是 的平分线,试探究
的平分线,试探究 ,
, ,
, 之间的等量关系,并证明你的结论.
之间的等量关系,并证明你的结论.

 中,
中, ,点
,点 是
是 的中点,若
的中点,若 是
是 的平分线,试判断
的平分线,试判断 ,
, ,
, 之间的等量关系.
之间的等量关系.解决此问题可以用如下方法:延长
 交
交 的延长线于点
的延长线于点 ,易证
,易证 得到
得到 ,从而把
,从而把 ,
, ,
, 转化在一个三角形中即可判断.
转化在一个三角形中即可判断. ,
, ,
, 之间的等量关系________;
之间的等量关系________;(2)问题探究:如图②,在四边形
 中,
中, ,
, 与
与 的延长线交于点
的延长线交于点 ,点
,点 是
是 的中点,若
的中点,若 是
是 的平分线,试探究
的平分线,试探究 ,
, ,
, 之间的等量关系,并证明你的结论.
之间的等量关系,并证明你的结论.
25.如图,在 中,
中, ,以
,以 为直径的
为直径的 与边
与边 ,
, 分别交于
分别交于 ,
, 两点,过点
两点,过点 作
作 于点
于点 .
.

(1)判断 与
与 的位置关系,并说明理由;
的位置关系,并说明理由;
(2)求证: 为
为 的中点;
的中点;
(3)若 ,
, ,求
,求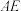 的长.
的长.
 中,
中, ,以
,以 为直径的
为直径的 与边
与边 ,
, 分别交于
分别交于 ,
, 两点,过点
两点,过点 作
作 于点
于点 .
.
(1)判断
 与
与 的位置关系,并说明理由;
的位置关系,并说明理由;(2)求证:
 为
为 的中点;
的中点;(3)若
 ,
, ,求
,求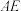 的长.
的长.26.如图,抛物线 与直线
与直线 分别相交于
分别相交于 ,
, 两点,且此抛物线与
两点,且此抛物线与 轴的一个交点为
轴的一个交点为 ,连接
,连接 ,
, .已知
.已知 ,
, .
.

(1)求抛物线的解析式;
(2)在抛物线对称轴 上找一点
上找一点 ,使
,使 的值最大,并求出这个最大值;
的值最大,并求出这个最大值;
(3)点 为
为 轴右侧抛物线上一动点,连接
轴右侧抛物线上一动点,连接 ,过点
,过点 作
作 交
交 轴于点
轴于点 ,问:是否存在点
,问:是否存在点 使得以
使得以 ,
, ,
, 为顶点的三角形与
为顶点的三角形与 相似?若存在,请求出所有符合条件的点
相似?若存在,请求出所有符合条件的点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
 与直线
与直线 分别相交于
分别相交于 ,
, 两点,且此抛物线与
两点,且此抛物线与 轴的一个交点为
轴的一个交点为 ,连接
,连接 ,
, .已知
.已知 ,
, .
.
(1)求抛物线的解析式;
(2)在抛物线对称轴
 上找一点
上找一点 ,使
,使 的值最大,并求出这个最大值;
的值最大,并求出这个最大值;(3)点
 为
为 轴右侧抛物线上一动点,连接
轴右侧抛物线上一动点,连接 ,过点
,过点 作
作 交
交 轴于点
轴于点 ,问:是否存在点
,问:是否存在点 使得以
使得以 ,
, ,
, 为顶点的三角形与
为顶点的三角形与 相似?若存在,请求出所有符合条件的点
相似?若存在,请求出所有符合条件的点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由. 搜索
搜索
 难度系数:0.94
难度系数:0.94  答案解析
答案解析
 有奖纠错
有奖纠错
