搜索
全一卷
难度系数：0.94 
答案解析
有奖纠错
1．数5的算术平方根为（ ）
A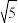． | B．25 | C．±25 | D．± |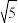
2．下列运算：sin30°=
，
.其中运算结果正确的个数为（）
，
.其中运算结果正确的个数为（）| A．4 | B．3 | C．2 | D．1 |
3．一元二次方程4x2+1=3x的根的情况是（ ）
A．没有实数根  | B．只有一个实数根 | C．有两个相等的实数根 | D．有两个不相等的实数根 |
4．如果式子
有意义，那么x的取值范围在数轴上表示出来，正确的是（ ）
有意义，那么x的取值范围在数轴上表示出来，正确的是（ ）A． | B． | C． | D． |
5．用配方法解一元二次方程
时，下列变形正确的为（ ）
时，下列变形正确的为（ ）A． | B． |
C． | D． |
6．如图，直线AC∥BD，AO、BO分别是∠BAC、∠ABD的平分线，那么∠BAO与∠ABO之间的大小关系一定为（ ）
| A．互余 | B．相等 | C．互补 | D．不等 |
7．在△ABC中，∠A∶∠B∶∠C=3∶4∶5,则∠C等于（ ）
| A．45° | B．60° | C．75° | D．90° |
8．顺次连接矩形ABCD各边的中点，所得四边形必定是（ ）
| A．邻边不等的平行四边形 | B．矩形 |
| C．正方形 | D．菱形 |
9．某校九年级数学兴趣小组的同学调查了若干名家长对“初中学生带手机上学”现象的看法，统计整理并制作了如下的条形与扇形统计图.
依据图中信息，得出下列结论：
（1）接受这次调查的家长人数为200人；
（2）在扇形统计图中，“不赞同”的家长部分所对应的扇形圆心角大小为162°；
（3）表示“无所谓”的家长人数为40人；
（4）随机抽查一名接受调查的家长，恰好抽到“很赞同”的家长的概率是
.
其中正确的结论个数为（ ）
依据图中信息，得出下列结论：
（1）接受这次调查的家长人数为200人；
（2）在扇形统计图中，“不赞同”的家长部分所对应的扇形圆心角大小为162°；
（3）表示“无所谓”的家长人数为40人；
（4）随机抽查一名接受调查的家长，恰好抽到“很赞同”的家长的概率是
.其中正确的结论个数为（ ）
| A．4 | B．3 | C．2 | D．1 |
10．如图，在直角∠O的内部有一滑动杆AB，当端点A沿直线AO向下滑动时，端点B会随之自动地沿直线OB向左滑动，如果滑动杆从图中AB处滑动到A′B′处，那么滑动杆的中点C所经过的路径是（ ）
| A．直线的一部分 | B．圆的一部分 | C．双曲线的一部分 | D．抛物线的一部分 |
11．若等腰直角三角形的外接圆半径的长为2，则其内切圆半径的长为（ ）
A． | B． | C． | D．—1 |
12．如图，在x轴的上方，直角∠BOA绕原点O按顺时针方向旋转．若∠BOA的两边分别与函数
、
的图象交于B、A两点，则∠OAB大小的变化趋势为（ ）
、
的图象交于B、A两点，则∠OAB大小的变化趋势为（ ）
| A．逐渐变小 | B．逐渐变大 | C．时大时小 | D．保持不变 |
13．计算（
+
）（﹣）的结果为__________ ．
+）（﹣）的结果为14．如图，菱形ABCD的边长为15，sin∠BAC=
，则对角线AC的长为____ .
，则对角线AC的长为
15．用2、3、4三个数字排成一个三位数，则排出的数是偶数的概率为______________ .
16．把直线
沿x轴向右平移2个单位，所得直线的函数解析式为_________________ .
沿x轴向右平移2个单位，所得直线的函数解析式为17．如图，在平面直角坐标系中，将矩形AOCD沿直线AE折叠（点E在边DC上），折叠后顶点D恰好落在边OC上的点F处.若点D的坐标为(10，8），则点E的坐标为 .
18．某服装厂专门安排210名工人进行手工衬衣的缝制，每件衬衣由2个衣袖、1个衣身、1个衣领组成，如果每人每天能够缝制衣袖10个或衣身15个或衣领12个，那么应该安排____ 名工人缝制衣袖，才能使每天缝制出的衣袖、衣身、衣领正好配套．
19．（本小题满分8分）化简：
.
.20．根据要求，解答下列问题.
（1）解下列方程组(直接写出方程组的解即可):
①
.
②
.
③
.
（2）以上每个方程组的解中，x值与y值的大小关系为 .
（3）请你构造一个具有以上外形特征的方程组，并直接写出它的解.
（1）解下列方程组(直接写出方程组的解即可):
①
.②
. ③
.（2）以上每个方程组的解中，x值与y值的大小关系为 .
（3）请你构造一个具有以上外形特征的方程组，并直接写出它的解.
21．如图,⊙O的直径AB的长为10，弦AC的长为5，∠ACB的平分线交⊙O于点
A． （1）求弧BC的长；（2）求弦BD的长. |
22．一种进价为每件40元的T恤，若销售单价为60元，则每周可卖出300件.为提高利润，欲对该T恤进行涨价销售.经过调查发现：每涨价1元，每周要少卖出10件.请确定该T恤涨价后每周的销售利润y（元）与销售单价x（元）之间的函数关系式，并求销售单价定为多少元时，每周的销售利润最大？
23．（本小题满分10分）如图，已知B、C、E三点在同一条直线上，△ABC与△DCE都是等边三角形.其中线段BD交AC于点G，线段AE交CD于点F.
求证：（1）△ACE≌△BCD；
（2）
.
求证：（1）△ACE≌△BCD；
（2）
.24．根据下列要求，解答相关问题.
（1）请补全以下求不等式-2x2-4x≥0的解集的过程.
①构造函数，画出图象：根据不等式特征构造二次函数y=-2x2-4x；并在下面的坐标系中(见图1)画出二次函数y=-2x2-4x的图象（只画出图象即可）.
②求得界点，标示所需：当y=0时，求得方程-2x2-4x=0的解为 ；并用锯齿线标示出函数y=-2x2-4x图象中y≥0的部分.
③借助图象，写出解集：由所标示图象，可得不等式-2x2-4x≥0的解集为 .
（2）利用（1）中求不等式解集的步骤，求不等式x2-2x+1<4的解集.
①构造函数，画出图象：
②求得界点，标示所需：
③借助图像，写出解集：
（3）参照以上两个求不等式解集的过程，借助一元二次方程的求根公式，直接写出关于x的不等式
ax2+bx+c>0(a>0)的解集.
（1）请补全以下求不等式-2x2-4x≥0的解集的过程.
①构造函数，画出图象：根据不等式特征构造二次函数y=-2x2-4x；并在下面的坐标系中(见图1)画出二次函数y=-2x2-4x的图象（只画出图象即可）.
②求得界点，标示所需：当y=0时，求得方程-2x2-4x=0的解为 ；并用锯齿线标示出函数y=-2x2-4x图象中y≥0的部分.
③借助图象，写出解集：由所标示图象，可得不等式-2x2-4x≥0的解集为 .
（2）利用（1）中求不等式解集的步骤，求不等式x2-2x+1<4的解集.
①构造函数，画出图象：
②求得界点，标示所需：
③借助图像，写出解集：
（3）参照以上两个求不等式解集的过程，借助一元二次方程的求根公式，直接写出关于x的不等式
ax2+bx+c>0(a>0)的解集.
