搜索
全一卷
难度系数：0.94 
答案解析
有奖纠错
1．在－2，－1，1，2这四个数中，最小的是( )
| A．－2 | B．－1 | C．1 | D．2 |
2．如图，直线a∥b，直线c与a、b相交，∠1＝70°，则∠2的大小是
| A．20° | B．50° | C．70° | D．110° |
3．如图所示的几何体，其主视图是（）
A． | B． | C． | D． |
4．2013年河池市初中毕业升学考试的考生人数约为3.2万名，从中抽取300名考生的数学成绩进行分析，在本次调查中，样本指的是（ ）
| A．300名考生的数学成绩 | B．300 |
| C．3.2万名考生的数学成绩 | D．300名考生 |
5．把不等式组
的解集表示在数轴上，正确的是
的解集表示在数轴上，正确的是A． | B． | C． | D． |
6．一个三角形的周长是36cm，则以这个三角形各边中点为顶点的三角形的周长是（ ）
| A．6cm | B．12cm | C．18cm | D．36cm |
7．下列运算正确的是
A． | B． | C． | D． |
8．如图（1），已知两个全等三角形的直角顶点及一条直角边重合．将△ACB绕点C按顺时针方向旋转到
的位置，其中
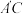交直线AD于点E，
分别交直线AD、AC于点F、G，则在图（2）中，全等三角形共有（ ）
的位置，其中
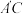交直线AD于点E，
分别交直线AD、AC于点F、G，则在图（2）中，全等三角形共有（ ）
| A．5对 | B．4对 | C．3对 | D．2对 |
9．如图，⊙O的弦AB垂直半径OC于点D，∠CBA＝30°，OC＝3
cm，则弦AB 的长为
cm，则弦AB 的长为
| A．9cm | B．3cm | C． cm | D． cm |
10．如图，AB为⊙O的直径，C为⊙O外一点，过点C作的⊙O切线，切点为B，连接AC交⊙O于D，∠C＝38°．点E在AB右侧的半圆上运动（不与A、B重合），则∠AED的大小是
| A．19° | B．38° | C．52° | D．76° |
11．如图，在直角梯形ABCD中，AB=2，BC=4，AD=6，M是CD的中点，点P在直角梯形的边上沿A→B→C→M运动，则△APM的面积y与点P经过的路程x之间的函数关系用图象表示是
A． | B． | C． | D． |
12．已知二次函数
，当自变量x取m对应的函数值大于0，设自变量分别取m－3，m＋3 时对应的函数值为y1，y2，则
，当自变量x取m对应的函数值大于0，设自变量分别取m－3，m＋3 时对应的函数值为y1，y2，则| A．y1＞0，y2＞0 | B．y1＞0，y2＜0 | C．y1＜0，y2＞0 | D．y1＜0，y2＜0 |
13．如果分式
有意义，那么x的取值范围是____________ ．
有意义，那么x的取值范围是14．分解因式：ax2－4a＝ ．
15．袋子中装有4个黑球2个白球，这些球的形状、大小、质地等完全相同．在看不到球的条件下，随机地从这个袋子中摸出一个球，这个球为白球的概率是___ ．
16．如图，点O是△ABC的两条角平分线的交点，若∠BOC＝118°，则∠A的大小是___ ．
17．如图，在
ABC中， AC＝6，BC＝5，sinA＝
，则tanB＝___ ．
ABC中， AC＝6，BC＝5，sinA＝，则tanB＝18．如图，正方形ABCD的边长为4，E、F分别是BC、CD上的两个动点，且AE⊥EF。则AF的最小值是 。
19．计算：
,(说明：本题不能使用计算器)
,(说明：本题不能使用计算器)20．先化简，再求值：
，其中x＝1．
，其中x＝1．21．请在图中补全坐标系及缺失的部分，并在横线上写恰当的内容．图中各点坐标如下：
，
，
，
．线段
上有一点M，使
，且相似比不等于1．求出点M的坐标并证明你的结论．
解：M（ ， ）
证明：∵
，
，
∴
度．
∵
，
，
∴
（ ），
（同理），
∴
． 
（同理）．
∴
．
在
与
中，
，
∴（如果一个三角形的两个角与另一个三角形的两个角对应相等，那么这两个三角形相似）．
，，，．线段上有一点M，使，且相似比不等于1．求出点M的坐标并证明你的结论． 解：M（ ， ）
证明：∵
，，∴
度．∵
，，∴
（ ），（同理），∴
． （同理）．∴
．在
与中，，∴
（如果一个三角形的两个角与另一个三角形的两个角对应相等，那么这两个三角形相似）．22．为响应“美丽河池 清洁乡村 美化校园”的号召，红水河中学计划在学校公共场所安装温馨提示牌和垃圾箱．已知，安装5个温馨提示牌和6个垃圾箱需730元，安装7个温馨提示牌和12个垃圾箱需1310元．
（1）安装1个温馨提示牌和1个垃圾箱各需多少元？
（2）安装8个温馨提示牌和15个垃圾箱共需多少元？
（1）安装1个温馨提示牌和1个垃圾箱各需多少元？
（2）安装8个温馨提示牌和15个垃圾箱共需多少元？
23．瑶寨中学食堂为学生提供了四种价格的午餐供其选择，这四种价格分别是：A：3元，B：4元，C：5元，D：6元。为了了解学生对四种午餐的购买情况，学校随机抽样调查了甲、乙两班学生某天购买四种午餐的情况，依据统计数据制成如下的统计图表：
甲、乙两班学生购买午餐的情况统计表 乙班购买午餐情况扇形统计图
（1）求乙班学生人数；
（2）求乙班购买午餐费用的中位数；
（3）已知甲、乙两班购买午餐费用的平均数为4.44元，从平均数和众数的角度分析，哪个班购买的午餐价格较高？
（4）从这次接受调查的学生中，随机抽查一人，恰好是购买C种午餐的学生的概率是多少？
甲、乙两班学生购买午餐的情况统计表 乙班购买午餐情况扇形统计图
（1）求乙班学生人数；
（2）求乙班购买午餐费用的中位数；
（3）已知甲、乙两班购买午餐费用的平均数为4.44元，从平均数和众数的角度分析，哪个班购买的午餐价格较高？
（4）从这次接受调查的学生中，随机抽查一人，恰好是购买C种午餐的学生的概率是多少？
24．华联超市欲购进A、B两种品牌的书包共400个．已知两种书包的进价和售价如下表所示．设购进A种书包x个，且所购进的两种书包能全部卖出，获得的总利润为w元．
（1）求w关于x的函数关系式；
（2）如果购进两种书包的总费不超过18000元，那么该商场如何进货才能获得最大利润？并求出最大利润．
（提示利润= 售价－进价）
品牌 | 进价（元/个） | 售价（元/个） |
A | 47 | 65 |
B | 37 | 50 |
（1）求w关于x的函数关系式；
（2）如果购进两种书包的总费不超过18000元，那么该商场如何进货才能获得最大利润？并求出最大利润．
（提示利润= 售价－进价）
25．如图（1），在
， 
，分别以、
为一边向外作正方形
、
，连结
、
，与交于点M．
(1)求证：
；
(2)如图（2），已知
，求四边形
的面积；
(3)在
中，设
，
，
，当
时，
．在任意中，
．就
，
的情形，探究k的取值范围（只需写出你得到的结论即可）．
， ，分别以、为一边向外作正方形、，连结、，与交于点M． (1)求证：
；(2)如图（2），已知
，求四边形的面积；(3)在
中，设，，，当时，．在任意中，．就，的情形，探究k的取值范围（只需写出你得到的结论即可）．26．已知：抛物线C1：y＝x2．如图（1），平移抛物线C1得到抛物线C2，C2经过C1的顶点O和A（2，0），C2的对称轴分别交C1、C2于点B、
A． （1）求抛物线C2的解析式； （2）探究四边形ODAB的形状并证明你的结论； （3）如图（2），将抛物线C2向下平移m个单位（m＞0）得抛物线C3，C3的顶点为G，与y轴交于M．点N是M关于x轴的对称点，点P（  ）在直线MG上．问：当m为何值时，在抛物线C3上存在点Q，使得以M、N、P、Q为顶点的四边形为平行四边形？ |
