全一卷
1.-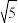 的绝对值是
的绝对值是________ , 的算术平方根是
的算术平方根是________ .
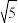 的绝对值是
的绝对值是 的算术平方根是
的算术平方根是2. =
=________ ;分解因式: =
=_______________ .
 =
= =
=3.关于 的一元二次方程
的一元二次方程 有一个根是
有一个根是 ,则
,则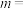
__________ .
 的一元二次方程
的一元二次方程 有一个根是
有一个根是 ,则
,则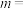
4.我省具有发展太阳能光伏发电产业得天独厚的条件.截止2015年,我省光伏并网发电容量将超过5000000千瓦,该数字用科学记数法可以表示为___________ 千瓦.
5.如图,直线a b,直线l与a相交于点P,与直线b相交于点Q,且PM垂直于l,若∠1=58°,则∠2=
b,直线l与a相交于点P,与直线b相交于点Q,且PM垂直于l,若∠1=58°,则∠2=_________ .

 b,直线l与a相交于点P,与直线b相交于点Q,且PM垂直于l,若∠1=58°,则∠2=
b,直线l与a相交于点P,与直线b相交于点Q,且PM垂直于l,若∠1=58°,则∠2=
6.若实数m,n满足 ,则
,则 =_____.
=_____.
 ,则
,则 =_____.
=_____.7.如图,三个小正方形的边长都为1,则图中阴影部分面积的和是 (结果保留π).

8.若将等腰直角三角形AOB按如图所示放置,OB=2,则点A关于原点对称的点的坐标为_________________ .


9.(2分)如图,点O为 所在圆的圆心,∠BOC=112°,点D在BA的延长线上,AD=AC,则∠D= .
所在圆的圆心,∠BOC=112°,点D在BA的延长线上,AD=AC,则∠D= .

 所在圆的圆心,∠BOC=112°,点D在BA的延长线上,AD=AC,则∠D= .
所在圆的圆心,∠BOC=112°,点D在BA的延长线上,AD=AC,则∠D= .
10.如图,在△ABC和△DEF中,点B、F、C、E在同一直线上,BF = CE,AC∥DF,请添加一个条件,使△ABC≌△DEF,这个添加的条件可以是________ .(只需写一个,不添加辅助线)


11.在一个不透明的袋子中装有红白两种颜色的球(形状大小质地完全相同)共25个,其中白球有5个。每次从中随机摸出一个球,并记下颜色后放回,那么从袋子中随机摸出一个红球的概率是____________。
12.如图是一组有规律的图案,图案1是由4个 组成的,图案2是由7个
组成的,图案2是由7个 组成的,那么图案5是由
组成的,那么图案5是由_______ 个 组成的,依此,第n个图案是由
组成的,依此,第n个图案是由___________ 个 组成的.
组成的.

 组成的,图案2是由7个
组成的,图案2是由7个 组成的,那么图案5是由
组成的,那么图案5是由 组成的,依此,第n个图案是由
组成的,依此,第n个图案是由 组成的.
组成的.
13.下列计算正确的是()
A. | B. |
C. | D. |
14.已知三角形两边的长分别是4和10,则此三角形第三边的长可能是()
| A.5 | B.6 | C.12 | D.16 |
15.在平行四边形ABCD中,点E是边AD上一点,且AE=2ED,EC交对角线BD于点F,则 等于()
等于()

 等于()
等于()
A. | B. | C. | D. |
16.甲、乙两人加工一批零件,甲完成120个与乙完成100个所用的时间相同,已知甲比乙每天多完成4个.设甲每天完成x个零件,依题意下面所列方程正确的是( )
A. | B. | C. | D. |
17.如图的几何体是由一个正方体切去一个小正方体形成的,它的主视图是( )


A. | B. | C. | D. |
18.甲、乙、丙、丁四位同学最近五次数学成绩统计如表,如果从这四位同学中,选出一位成绩较好且状态稳定的同学参加即将举行的中学生数学竞赛,那么应选( )


| A.甲 | B.乙 | C.丙 | D.丁 |
19.(3分)已知一次函数 与反比例函数
与反比例函数 ,那么它们在同一坐标系中的图象可能是()
,那么它们在同一坐标系中的图象可能是()
 与反比例函数
与反比例函数 ,那么它们在同一坐标系中的图象可能是()
,那么它们在同一坐标系中的图象可能是()A. | B. | C. | D. |
20.一副三角板叠在一起如图放置,最小锐角的顶点D恰好放在等腰直角三角板的斜边上,AC与
DM、DN分别交于点E、F,把△MDN绕点D旋转到一定位置,使得DE=DF,则∠BDN的度数是
( )
DM、DN分别交于点E、F,把△MDN绕点D旋转到一定位置,使得DE=DF,则∠BDN的度数是
( )
| A.105° | B.115° | C.120° | D.135° |
21.(5分)计算: .
.
 .
.22.(7分)先化简再求值: ,其中
,其中 .
.
 ,其中
,其中 .
.23.(8分)如图,为测量某建筑物BC上旗杆AB的高度,小明在距离建筑物BC底部11.4米的点F处,测得视线与水平线夹角∠AED=60°,∠BED=45°.小明的观测点与地面的距离EF为1.6米.

(1)求建筑物BC的高度;
(2)求旗杆AB的高度(结果精确到0.1米).
参考数据: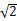 ≈1.41,
≈1.41, ≈1.73.
≈1.73.

(1)求建筑物BC的高度;
(2)求旗杆AB的高度(结果精确到0.1米).
参考数据:
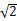 ≈1.41,
≈1.41, ≈1.73.
≈1.73.24.(8分)如图,梯形ABCD中,AB∥DC,AC平分∠BAD,CE∥DA交AB于点E.求证:四边形ADCE是菱形.

25.某玩具商计划生产A,B两种型号的玩具投入市场,初期计划生产100件,生产投入资金不少于22400元,但不超过22500元,且资金要全部投入到生产这两种型号的玩具.假设生产的这两种型号的玩具能全部售出,这两种玩具的生产成本和售价如下表:
(1)该玩具商对这两种型号玩具有哪几种生产方案?
(2)求该玩具商所能获得的最大利润.
| 型号 | A | B |
| 成本(元) | 200 | 240 |
| 售价(元) | 250 | 300 |
(1)该玩具商对这两种型号玩具有哪几种生产方案?
(2)求该玩具商所能获得的最大利润.
26.如图,在△ABC中,∠B=60°,⊙O是△ABC的外接圆,过点A作⊙O的切线,交CO的延长线于点M,CM交⊙O于点D.
(1)求证:AM=AC;
(2)若AC=3,求MC的长.

(1)求证:AM=AC;
(2)若AC=3,求MC的长.

27.为了解全校学生上学的交通方式,该校九年级(8)班的5名同学联合设计了一份调查问卷,对该校部分学生进行了随机调查.按A(骑自行车)、B(乘公交车)、C(步行)、D(乘私家车)、E(其他方式)设置选项,要求被调查同学从中单选.并将调查结果绘制成条形统计图1和扇形统计图2,根据以上信息,解答下列问题:

(1)本次接受调查的总人数是 人,并把条形统计图补充完整;
(2)在扇形统计图中,“步行”的人数所占的百分比是 ,“其他方式”所在扇形的圆心角度数是 ;
(3)已知这5名同学中有2名女同学,要从中选两名同学汇报调查结果.请你用列表法或画树状图的方法,求出恰好选出1名男生和1名女生的概率.

(1)本次接受调查的总人数是 人,并把条形统计图补充完整;
(2)在扇形统计图中,“步行”的人数所占的百分比是 ,“其他方式”所在扇形的圆心角度数是 ;
(3)已知这5名同学中有2名女同学,要从中选两名同学汇报调查结果.请你用列表法或画树状图的方法,求出恰好选出1名男生和1名女生的概率.
28.如图,二次函数 的图象与
的图象与 轴交于
轴交于 ,
, 两点,与
两点,与 轴交于点
轴交于点 .该抛物线的顶点为
.该抛物线的顶点为 .
.

(1)求该抛物线的解析式;
(2)判断 的形状,并说明理由.
的形状,并说明理由.
(3)探究坐标轴上是否存在点 ,使得以点
,使得以点 ,
, ,
, 为顶点的三角形与
为顶点的三角形与 相似?若存在,请求出点
相似?若存在,请求出点 的坐标,若不存在,请说明理由.
的坐标,若不存在,请说明理由.
 的图象与
的图象与 轴交于
轴交于 ,
, 两点,与
两点,与 轴交于点
轴交于点 .该抛物线的顶点为
.该抛物线的顶点为 .
.
(1)求该抛物线的解析式;
(2)判断
 的形状,并说明理由.
的形状,并说明理由.(3)探究坐标轴上是否存在点
 ,使得以点
,使得以点 ,
, ,
, 为顶点的三角形与
为顶点的三角形与 相似?若存在,请求出点
相似?若存在,请求出点 的坐标,若不存在,请说明理由.
的坐标,若不存在,请说明理由. 搜索
搜索
 难度系数:0.85
难度系数:0.85  答案解析
答案解析
 有奖纠错
有奖纠错
