全一卷
1.计算 ()
()
 ()
()A. | B.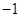 | C.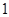 | D. |
2.2007年5月2日,南京夫子庙、中山陵、玄武湖、雨花台四大景区共接待游客约518 000人,这个数可用科学记数法表示为()
A. | B. | C. | D. |
3.计算 的结果是()
的结果是()
 的结果是()
的结果是()A. | B. | C. | D. |
4. 的算术平方根为( )
的算术平方根为( )
 的算术平方根为( )
的算术平方根为( )A. | B. | C. | D.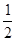 |
5.不等式组 的解集是()
的解集是()
 的解集是()
的解集是()A. | B. | C. | D. |
6.反比例函数 (
( 为常数,
为常数, )的图象位于( )
)的图象位于( )
 (
( 为常数,
为常数, )的图象位于( )
)的图象位于( )| A.第一、二象限 | B.第一、三象限 |
| C.第二、四象限 | D.第三、四象限 |
7.如图,一个可以自由转动的转盘被等分成6个扇形区域,并涂上了相应 的颜色,转动转盘,转盘停止后,指针指向黄色区域的概率是 ( )


A. | B. |
C. | D. |
8.下列轴对称图形中,对称轴条数最少的是( )
| A.等边三角形 | B.正方形 | C.正六边形 | D.圆 |
9.下列四个几何体中,已知某个几何体的主视图、左视图、俯视图分别为长方形、长方形、圆,则该几何体是( )
A.球体  | B.长方体  | C.圆锥体  | D.圆柱体 |
10.如果 是等腰直角三角形的一个锐角,则
是等腰直角三角形的一个锐角,则 的值是()
的值是()
 是等腰直角三角形的一个锐角,则
是等腰直角三角形的一个锐角,则 的值是()
的值是()A. | B. | C. | D.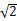 |
11.下列各数与2- 相乘,结果为有理数的是( )
相乘,结果为有理数的是( )
 相乘,结果为有理数的是( )
相乘,结果为有理数的是( )A. +2 +2 | B.2- | C.-2+ | D. |
12.如图,在平面直角坐标系中,点 在第一象限,
在第一象限, 与
与 轴相切于点
轴相切于点 ,与
,与 轴交于
轴交于 ,
, 两点,则点
两点,则点 的坐标是()
的坐标是()

 在第一象限,
在第一象限, 与
与 轴相切于点
轴相切于点 ,与
,与 轴交于
轴交于 ,
, 两点,则点
两点,则点 的坐标是()
的坐标是()
A. | B. | C. | D. |
13.如果 ,那么
,那么 的补角等于 .
的补角等于 .
 ,那么
,那么 的补角等于 .
的补角等于 .14.已知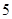 筐苹果的质量分别为(单位:
筐苹果的质量分别为(单位: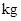 );
); ,则这5筐苹果的平均质量为
,则这5筐苹果的平均质量为______________ 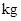 .
.
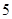 筐苹果的质量分别为(单位:
筐苹果的质量分别为(单位: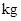 );
); ,则这5筐苹果的平均质量为
,则这5筐苹果的平均质量为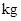 .
.15.如图,⊙O是△ABC的外接圆,∠C=30°,AB=2cm,则⊙O的半径为________cm.

16.已知点 位于第二象限,并且
位于第二象限,并且 ,
, 为整数,写出一个符合上述条件的点
为整数,写出一个符合上述条件的点 的坐标:
的坐标:______ .
 位于第二象限,并且
位于第二象限,并且 ,
, 为整数,写出一个符合上述条件的点
为整数,写出一个符合上述条件的点 的坐标:
的坐标:17.解方程组:

18.计算: .
.
 .
.19.某养鸡场分3次用鸡蛋孵化出小鸡,每次孵化所用的鸡蛋数、每次的孵化率(孵化率
 )分别如图1,图2所示:
)分别如图1,图2所示:

(1)求该养鸡场这3次孵化出的小鸡总数和平均孵化率;
(2)如果要孵化出2000只小鸡,根据上面的计算结果,估计该养鸡场要用多少个鸡蛋?

 )分别如图1,图2所示:
)分别如图1,图2所示:
(1)求该养鸡场这3次孵化出的小鸡总数和平均孵化率;
(2)如果要孵化出2000只小鸡,根据上面的计算结果,估计该养鸡场要用多少个鸡蛋?
20.两组邻边分别相等的四边形我们称它为菱形.
如图,在菱形 中,
中, ,
, ,
,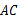 ,
,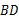 相交于点
相交于点 ,
,

(1)求证:① ;
;
② ,
, ;
;
(2)如果 ,
, ,求菱形
,求菱形 的面积.
的面积.
如图,在菱形
 中,
中, ,
, ,
,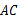 ,
,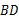 相交于点
相交于点 ,
,
(1)求证:①
 ;
;②
 ,
, ;
;(2)如果
 ,
, ,求菱形
,求菱形 的面积.
的面积.21.将 四人随机分成甲、乙两组参加羽毛球比赛,每组两人.
四人随机分成甲、乙两组参加羽毛球比赛,每组两人.
(1) 在甲组的概率是多少?
在甲组的概率是多少?
(2) 都在甲组的概率是多少?
都在甲组的概率是多少?
 四人随机分成甲、乙两组参加羽毛球比赛,每组两人.
四人随机分成甲、乙两组参加羽毛球比赛,每组两人.(1)
 在甲组的概率是多少?
在甲组的概率是多少?(2)
 都在甲组的概率是多少?
都在甲组的概率是多少?22.如图,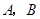 两地之间有一座山,汽车原来从
两地之间有一座山,汽车原来从 地到
地到 地须经
地须经 地沿折线
地沿折线 行驶,现开通隧道后,汽车直接沿直线
行驶,现开通隧道后,汽车直接沿直线 行驶.已知
行驶.已知 ,
, ,
, ,则隧道开通后,汽车从
,则隧道开通后,汽车从 地到
地到 地比原来少走多少千米?(结果精确到
地比原来少走多少千米?(结果精确到 )(参考数据:
)(参考数据: ,
, )
)
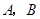 两地之间有一座山,汽车原来从
两地之间有一座山,汽车原来从 地到
地到 地须经
地须经 地沿折线
地沿折线 行驶,现开通隧道后,汽车直接沿直线
行驶,现开通隧道后,汽车直接沿直线 行驶.已知
行驶.已知 ,
, ,
, ,则隧道开通后,汽车从
,则隧道开通后,汽车从 地到
地到 地比原来少走多少千米?(结果精确到
地比原来少走多少千米?(结果精确到 )(参考数据:
)(参考数据: ,
, )
)
23.某市为了鼓励居民节约用水,采用分段计费的方法按月计算每户家庭的水费,月用水量不超过20 时,按2元/
时,按2元/ 计费;月用水量超过20
计费;月用水量超过20 时,其中的20
时,其中的20 仍按2元/
仍按2元/ 收费,超过部分按
收费,超过部分按 元/
元/ 计费.设每户家庭用用水量为
计费.设每户家庭用用水量为 时,应交水费
时,应交水费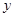 元.
元.
(1)分别求出 和
和 时
时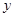 与
与 的函数表达式;
的函数表达式;
(2)小明家第二季度交纳水费的情况如下:
小明家这个季度共用水多少立方米?
 时,按2元/
时,按2元/ 计费;月用水量超过20
计费;月用水量超过20 时,其中的20
时,其中的20 仍按2元/
仍按2元/ 收费,超过部分按
收费,超过部分按 元/
元/ 计费.设每户家庭用用水量为
计费.设每户家庭用用水量为 时,应交水费
时,应交水费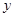 元.
元.(1)分别求出
 和
和 时
时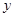 与
与 的函数表达式;
的函数表达式;(2)小明家第二季度交纳水费的情况如下:
| 月份 | 四月份 | 五月份 | 六月份 |
| 交费金额 | 30元 | 34元 | 42.6元 |
24.如图, 是半径为
是半径为 的
的 上的定点,动点
上的定点,动点 从
从 出发,以
出发,以 的速度沿圆周逆时针运动,当点
的速度沿圆周逆时针运动,当点 回到
回到 地立即停止运动.
地立即停止运动.

(1)如果 ,求点
,求点 运动的时间;
运动的时间;
(2)如果点B是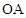 延长线上的一点,
延长线上的一点, ,那么当点
,那么当点 运动的时间为
运动的时间为 时,判断直线BP与
时,判断直线BP与 的位置关系,并说明理由.
的位置关系,并说明理由.
 是半径为
是半径为 的
的 上的定点,动点
上的定点,动点 从
从 出发,以
出发,以 的速度沿圆周逆时针运动,当点
的速度沿圆周逆时针运动,当点 回到
回到 地立即停止运动.
地立即停止运动.
(1)如果
 ,求点
,求点 运动的时间;
运动的时间;(2)如果点B是
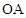 延长线上的一点,
延长线上的一点, ,那么当点
,那么当点 运动的时间为
运动的时间为 时,判断直线BP与
时,判断直线BP与 的位置关系,并说明理由.
的位置关系,并说明理由.25.某农场去年种植了10亩地的南瓜,亩产量为2000 ,根据市场需要,今年该农场扩大了种植面积,并且全部种植了高产的新品种南瓜,已知南瓜种植面积的增长率是亩产量的增长率的2倍,今年南瓜的总产量为60 000kg,求南瓜亩产量的增长率.
,根据市场需要,今年该农场扩大了种植面积,并且全部种植了高产的新品种南瓜,已知南瓜种植面积的增长率是亩产量的增长率的2倍,今年南瓜的总产量为60 000kg,求南瓜亩产量的增长率.
 ,根据市场需要,今年该农场扩大了种植面积,并且全部种植了高产的新品种南瓜,已知南瓜种植面积的增长率是亩产量的增长率的2倍,今年南瓜的总产量为60 000kg,求南瓜亩产量的增长率.
,根据市场需要,今年该农场扩大了种植面积,并且全部种植了高产的新品种南瓜,已知南瓜种植面积的增长率是亩产量的增长率的2倍,今年南瓜的总产量为60 000kg,求南瓜亩产量的增长率.26.在梯形 中,
中, ,
, ,
, ,点
,点 分别在线段
分别在线段 上(点
上(点 与点
与点 不重合),且
不重合),且 ,设
,设 ,
, .
.

(1)求 与
与 的函数表达式;
的函数表达式;
(2)当 为何值时,
为何值时, 有最大值,最大值是多少?
有最大值,最大值是多少?
 中,
中, ,
, ,
, ,点
,点 分别在线段
分别在线段 上(点
上(点 与点
与点 不重合),且
不重合),且 ,设
,设 ,
, .
.
(1)求
 与
与 的函数表达式;
的函数表达式;(2)当
 为何值时,
为何值时, 有最大值,最大值是多少?
有最大值,最大值是多少?27.在平面内,先将一个多边形以点 为位似中心放大或缩小,使所得多边形与原多边形对应线段的比为
为位似中心放大或缩小,使所得多边形与原多边形对应线段的比为 ,并且原多边形上的任一点
,并且原多边形上的任一点 ,它的对应点
,它的对应点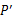 在线段
在线段 或其延长线上;接着将所得多边形以点
或其延长线上;接着将所得多边形以点 为旋转中心,逆时针旋转一个角度
为旋转中心,逆时针旋转一个角度 ,这种经过和旋转的图形变换叫做旋转相似变换,记为
,这种经过和旋转的图形变换叫做旋转相似变换,记为 ,其中点
,其中点 叫做旋转相似中心,
叫做旋转相似中心, 叫做相似比,
叫做相似比, 叫做旋转角.
叫做旋转角.
(1)填空:
①如图1,将 以点
以点 为旋转相似中心,放大为原来的2倍,再逆时针旋转
为旋转相似中心,放大为原来的2倍,再逆时针旋转 ,得到
,得到 ,这个旋转相似变换记为
,这个旋转相似变换记为 ( , );
( , );
②如图2, 是边长为
是边长为 的等边三角形,将它作旋转相似变换
的等边三角形,将它作旋转相似变换 ,得到
,得到 ,则线段
,则线段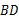 的长为
的长为  ;
;
(2)如图3,分别以锐角三角形 的三边
的三边 ,
, ,
, 为边向外作正方形
为边向外作正方形 ,
, ,
, ,点
,点 ,
, ,
, 分别是这三个正方形的对角线交点,试分别利用
分别是这三个正方形的对角线交点,试分别利用 与
与 ,
, 与
与 之间的关系,运用旋转相似变换的知识说明线段
之间的关系,运用旋转相似变换的知识说明线段 与
与 之间的关系.
之间的关系.
 为位似中心放大或缩小,使所得多边形与原多边形对应线段的比为
为位似中心放大或缩小,使所得多边形与原多边形对应线段的比为 ,并且原多边形上的任一点
,并且原多边形上的任一点 ,它的对应点
,它的对应点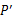 在线段
在线段 或其延长线上;接着将所得多边形以点
或其延长线上;接着将所得多边形以点 为旋转中心,逆时针旋转一个角度
为旋转中心,逆时针旋转一个角度 ,这种经过和旋转的图形变换叫做旋转相似变换,记为
,这种经过和旋转的图形变换叫做旋转相似变换,记为 ,其中点
,其中点 叫做旋转相似中心,
叫做旋转相似中心, 叫做相似比,
叫做相似比, 叫做旋转角.
叫做旋转角.(1)填空:
①如图1,将
 以点
以点 为旋转相似中心,放大为原来的2倍,再逆时针旋转
为旋转相似中心,放大为原来的2倍,再逆时针旋转 ,得到
,得到 ,这个旋转相似变换记为
,这个旋转相似变换记为 ( , );
( , );②如图2,
 是边长为
是边长为 的等边三角形,将它作旋转相似变换
的等边三角形,将它作旋转相似变换 ,得到
,得到 ,则线段
,则线段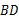 的长为
的长为  ;
;(2)如图3,分别以锐角三角形
 的三边
的三边 ,
, ,
, 为边向外作正方形
为边向外作正方形 ,
, ,
, ,点
,点 ,
, ,
, 分别是这三个正方形的对角线交点,试分别利用
分别是这三个正方形的对角线交点,试分别利用 与
与 ,
, 与
与 之间的关系,运用旋转相似变换的知识说明线段
之间的关系,运用旋转相似变换的知识说明线段 与
与 之间的关系.
之间的关系.
28.已知直线 及
及 外一点
外一点 ,分别按下列要求写出画法,并保留两图痕迹.
,分别按下列要求写出画法,并保留两图痕迹.
(1)在图1中,只用圆规在直线 上画出两点
上画出两点 ,使得点
,使得点 是一个等腰三角形的三个顶点;
是一个等腰三角形的三个顶点;
(2)在图2中,只用圆规在直线 外画出一点
外画出一点 ,使得点
,使得点 所在直线与直线
所在直线与直线 平行.
平行.

 及
及 外一点
外一点 ,分别按下列要求写出画法,并保留两图痕迹.
,分别按下列要求写出画法,并保留两图痕迹.(1)在图1中,只用圆规在直线
 上画出两点
上画出两点 ,使得点
,使得点 是一个等腰三角形的三个顶点;
是一个等腰三角形的三个顶点;(2)在图2中,只用圆规在直线
 外画出一点
外画出一点 ,使得点
,使得点 所在直线与直线
所在直线与直线 平行.
平行.
 搜索
搜索
 难度系数:0.94
难度系数:0.94  答案解析
答案解析
 有奖纠错
有奖纠错
