搜索
为位似中心放大或缩小，使所得多边形与原多边形对应线段的比为
，并且原多边形上的任一点
，它的对应点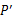
在线段
或其延长线上；接着将所得多边形以点为旋转中心，逆时针旋转一个角度
，这种经过和旋转的图形变换叫做旋转相似变换，记为
，其中点叫做旋转相似中心，叫做相似比，叫做旋转角．（1）填空：
①如图1，将
以点
为旋转相似中心，放大为原来的2倍，再逆时针旋转
，得到
，这个旋转相似变换记为（ ， ）；②如图2，
是边长为
的等边三角形，将它作旋转相似变换
，得到，则线段
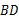的长为 
；（2）如图3，分别以锐角三角形
的三边
，
，
为边向外作正方形
，
，
，点
，
，
分别是这三个正方形的对角线交点，试分别利用
与
，
与
之间的关系，运用旋转相似变换的知识说明线段
与
之间的关系．
同类型试题
y = sin x， x∈R， y∈[–1，1]，周期为2π，函数图像以 x = (π/2) + kπ 为对称轴
y = arcsin x， x∈[–1，1]， y∈[–π/2，π/2]
sin x = 0 ←→ arcsin x = 0
sin x = 1/2 ←→ arcsin x = π/6
sin x = √2/2 ←→ arcsin x = π/4
sin x = 1 ←→ arcsin x = π/2
y = sin x， x∈R， y∈[–1，1]，周期为2π，函数图像以 x = (π/2) + kπ 为对称轴
y = arcsin x， x∈[–1，1]， y∈[–π/2，π/2]
sin x = 0 ←→ arcsin x = 0
sin x = 1/2 ←→ arcsin x = π/6
sin x = √2/2 ←→ arcsin x = π/4
sin x = 1 ←→ arcsin x = π/2
