全一卷
1.﹣3的绝对值是( )
| A.﹣3 | B.3 | C.- | D. |
2.在长春市“暖房子工程”实施过程中,某工程队做了面积为632000的外墙保暖,632000这个数用科学记数法表示为 ( )
A. | B. | C. | D. |
3.计算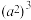 的结果是( )
的结果是( )
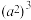 的结果是( )
的结果是( )A. | B. | C. | D. |
4.图中的两个圆柱体底面半径相同而高度不同,关于这两个圆柱体的视图说法正确的是()
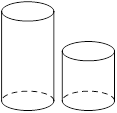

| A.主视图相同 | B.俯视图相同 |
| C.左视图相同 | D.主视图、俯视图、左视图都相同 |
5.方程x2﹣2x+3=0的根的情况是( )
| A.有两个相等的实数根 | B.只有一个实数根 |
| C.没有实数根 | D.有两个不相等的实数根 |
6.如图,在 中,
中, 过
过 点作
点作 若
若 则
则 的大小为( )
的大小为( )

 中,
中, 过
过 点作
点作 若
若 则
则 的大小为( )
的大小为( )
A. | B. | C. | D. |
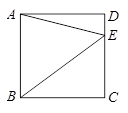
7.如图,四边形ABCD内接于⊙O,若四边形ABCO是平行四边形,则∠ADC的大小为( )


A. | B. | C. | D. |
8.如图,在平面直角坐标系中,点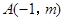 在直线
在直线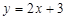 上.连结
上.连结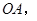 将线段
将线段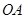 绕点
绕点 顺时针旋转
顺时针旋转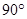 ,点
,点 的对应点
的对应点 恰好落在直线
恰好落在直线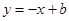 上,则
上,则 的值为()
的值为()
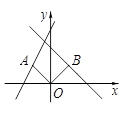
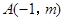 在直线
在直线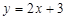 上.连结
上.连结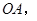 将线段
将线段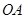 绕点
绕点 顺时针旋转
顺时针旋转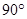 ,点
,点 的对应点
的对应点 恰好落在直线
恰好落在直线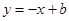 上,则
上,则 的值为()
的值为()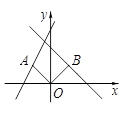
A.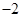 | B.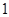 | C.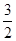 | D. |
9.比较大小:
_______  .(填“>”,“<”或“=”)
.(填“>”,“<”或“=”)

 .(填“>”,“<”或“=”)
.(填“>”,“<”或“=”)10.不等式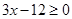 的解集为
的解集为_______ .
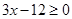 的解集为
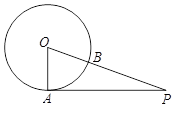
的解集为11.如图,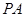 为
为 的切线,
的切线, 为切点,
为切点, 是
是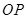 与
与 的交点,若
的交点,若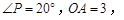 则
则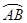 的长为 (结果保留
的长为 (结果保留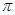 ).
).
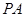 为
为 的切线,
的切线, 为切点,
为切点, 是
是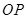 与
与 的交点,若
的交点,若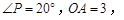 则
则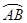 的长为 (结果保留
的长为 (结果保留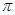 ).
).
12.如图,在平面直角坐标系中,点 在函数
在函数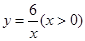 的图象上,过点
的图象上,过点 分别作
分别作 轴、
轴、 轴的垂线,垂足分别为
轴的垂线,垂足分别为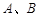 ,取线段
,取线段 的中点
的中点 ,连结
,连结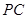 并延长交
并延长交 轴于点
轴于点 ,则
,则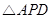 的面积为 .
的面积为 .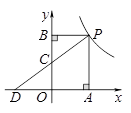
 在函数
在函数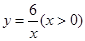 的图象上,过点
的图象上,过点 分别作
分别作 轴、
轴、 轴的垂线,垂足分别为
轴的垂线,垂足分别为 ,取线段
,取线段 的中点
的中点 ,连结
,连结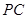 并延长交
并延长交 轴于点
轴于点 ,则
,则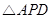 的面积为 .
的面积为 .
13.如图,点 在正方形
在正方形 的边
的边 上,若
上,若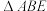 的面积为
的面积为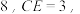 则线段
则线段 的长为
的长为_______ .
 在正方形
在正方形 的边
的边 上,若
上,若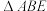 的面积为
的面积为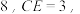 则线段
则线段 的长为
的长为
14.如图,在平面直角坐标系中,点 在抛物线
在抛物线 上运动,过点
上运动,过点 作
作 轴于点
轴于点 ,以
,以 为对角线作矩形
为对角线作矩形 ,连结
,连结 ,则对角线
,则对角线 的最小值为
的最小值为_______ .

 在抛物线
在抛物线 上运动,过点
上运动,过点 作
作 轴于点
轴于点 ,以
,以 为对角线作矩形
为对角线作矩形 ,连结
,连结 ,则对角线
,则对角线 的最小值为
的最小值为
15.先化简,再求值: 其中
其中 .
.
 其中
其中 .
.16.一个不透明的盒子中有三张卡片,卡片上面分别标有字母a,b,c,每张卡片除字母不同外其他都相同,小玲先从盒子中随机抽出一张卡片,记下字母后放回并搅匀;再从盒子中随机抽出一张卡片并记下字母,用画树状图(或列表)的方法,求小玲两次抽出的卡片上的字母相同的概率.
17.为了美化环境,某地政府计划对辖区内60km2的土地进行绿化,为了尽快完成任务,实际平均每月的绿化面积是原计划的1.5倍,结果提前2个月完成任务,求原计划平均每月的绿化面积.
18.如图, 是
是 外角
外角 的平分线,
的平分线, 交于
交于 点交于点
点交于点 ,
, 交于
交于 点交于点
点交于点 ,求证:四边形
,求证:四边形 是菱形.
是菱形.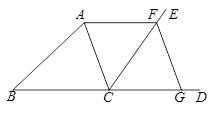
 是
是 外角
外角 的平分线,
的平分线, 交于
交于 点交于点
点交于点 ,
, 交于
交于 点交于点
点交于点 ,求证:四边形
,求证:四边形 是菱形.
是菱形.
19.如图,海上 两岛分别位于
两岛分别位于 岛的正东和正北方向,一艘船从
岛的正东和正北方向,一艘船从 岛出发,以18海里/时的速度向正北方向航行2小时到达
岛出发,以18海里/时的速度向正北方向航行2小时到达 岛,此时测得
岛,此时测得 岛在
岛在 岛的南偏东
岛的南偏东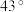 ,求
,求 两岛之间的距离.(结果精确到0.1海里)
两岛之间的距离.(结果精确到0.1海里)
【参考数据: 】
】

 两岛分别位于
两岛分别位于 岛的正东和正北方向,一艘船从
岛的正东和正北方向,一艘船从 岛出发,以18海里/时的速度向正北方向航行2小时到达
岛出发,以18海里/时的速度向正北方向航行2小时到达 岛,此时测得
岛,此时测得 岛在
岛在 岛的南偏东
岛的南偏东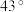 ,求
,求 两岛之间的距离.(结果精确到0.1海里)
两岛之间的距离.(结果精确到0.1海里)【参考数据:
 】
】
20.在“世界家庭日”前夕,某校团委随机抽取n名本校学生,对“世界家庭日”当天所喜欢的家庭活动方式进行问卷调查.问卷中的家庭活动方式包括:
A.在家里聚餐 B.去影院看电影
C.到公园游玩 D.进行其他活动
每位学生在问卷调查时都按要求只选择了其中一种喜欢的活动方式.该校团委收回全部问卷后,将收集到的数据整理并绘制成如下的统计图.根据统计图提供的信息,解答下列问题:
n名学生喜欢的家庭活动方式的人数条形统计图

(1)求n的值;
(2)四种方式中最受学生喜欢的方式为C(用A,B,C,D作答);选择该种方式的学生人数占被调查的学生人数的百分比为______;
(3)根据统计结果,估计该校1 800名学生中喜欢C方式的学生比喜欢B方式的学生多的人数.
21.甲、乙两台机器共同加工一批零件,在加工过程中两台机器均改变了一次工作效率,从工作开始到加工完这批零件两台机器恰好同时工作6小时,甲、乙两台机器各自加工的零件的个数 (个)与加工时间
(个)与加工时间 (时)之间的函数图象分别为折线
(时)之间的函数图象分别为折线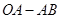 与折线
与折线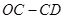 ,如图所示.
,如图所示.
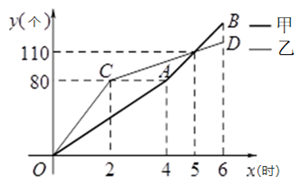
(1)求甲机器改变工作效率前每小时加工零件的个数;
(2)求乙机器改变工作效率后 与
与 之间的函数关系式;
之间的函数关系式;
(3)求这批零件的总个数.
 (个)与加工时间
(个)与加工时间 (时)之间的函数图象分别为折线
(时)之间的函数图象分别为折线 与折线
与折线 ,如图所示.
,如图所示.
(1)求甲机器改变工作效率前每小时加工零件的个数;
(2)求乙机器改变工作效率后
 与
与 之间的函数关系式;
之间的函数关系式;(3)求这批零件的总个数.
22.在矩形 中,已知
中,已知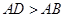 ,在边
,在边 上取点
上取点 ,使
,使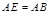 ,连结
,连结 ,过点
,过点 作
作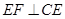 ,与边
,与边 或其延长线交于点
或其延长线交于点 .
.
猜想:如图①,当点 在边
在边 上时,线段
上时,线段 与
与 的大小关系为 .
的大小关系为 .
探究:如图②,当点 在边
在边 的延长线上时,
的延长线上时,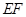 与边
与边 交于点
交于点 .判断线段
.判断线段 与
与 的大小关系,并加以证明.
的大小关系,并加以证明.
应用:如图②,若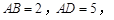 利用探究得到的结论,求线段
利用探究得到的结论,求线段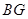 的长.
的长.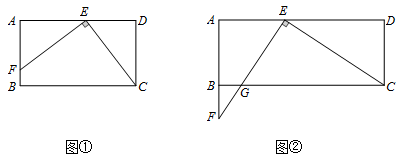
 中,已知
中,已知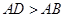 ,在边
,在边 上取点
上取点 ,使
,使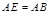 ,连结
,连结 ,过点
,过点 作
作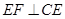 ,与边
,与边 或其延长线交于点
或其延长线交于点 .
.猜想:如图①,当点
 在边
在边 上时,线段
上时,线段 与
与 的大小关系为 .
的大小关系为 .探究:如图②,当点
 在边
在边 的延长线上时,
的延长线上时,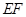 与边
与边 交于点
交于点 .判断线段
.判断线段 与
与 的大小关系,并加以证明.
的大小关系,并加以证明.应用:如图②,若
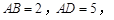 利用探究得到的结论,求线段
利用探究得到的结论,求线段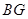 的长.
的长.
23.如图,在等边 中,
中,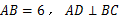 于点
于点 ,点
,点 在边
在边 上运动,过点
上运动,过点 作
作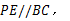 与边
与边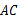 交于点
交于点 ,连结
,连结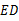 ,以
,以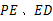 为邻边作□
为邻边作□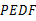 ,设□
,设□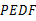 与
与 重叠部分图形的面积为
重叠部分图形的面积为 ,线段
,线段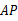 的长为
的长为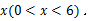
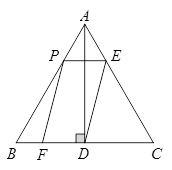
(1)求线段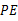 的长(用含
的长(用含 的代数式表示);
的代数式表示);
(2)当四边形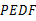 为菱形时,求
为菱形时,求 的值;
的值;
(3)求 与
与 之间的函数关系式;
之间的函数关系式;
(4)设点 关于直线
关于直线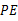 的对称点为点
的对称点为点 ,当线段
,当线段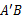 的垂直平分线与直线
的垂直平分线与直线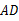 相交时,设其交点为
相交时,设其交点为 ,当点
,当点 与点
与点 位于直线
位于直线 同侧(不包括点
同侧(不包括点 在直线
在直线 上)时,直接写出
上)时,直接写出 的取值范围.
的取值范围.
 中,
中,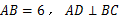 于点
于点 ,点
,点 在边
在边 上运动,过点
上运动,过点 作
作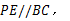 与边
与边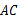 交于点
交于点 ,连结
,连结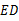 ,以
,以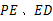 为邻边作□
为邻边作□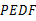 ,设□
,设□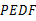 与
与 重叠部分图形的面积为
重叠部分图形的面积为 ,线段
,线段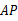 的长为
的长为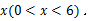
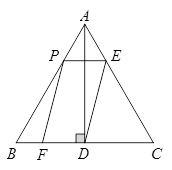
(1)求线段
 的长(用含
的长(用含 的代数式表示);
的代数式表示);(2)当四边形
 为菱形时,求
为菱形时,求 的值;
的值;(3)求
 与
与 之间的函数关系式;
之间的函数关系式;(4)设点
 关于直线
关于直线 的对称点为点
的对称点为点 ,当线段
,当线段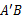 的垂直平分线与直线
的垂直平分线与直线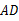 相交时,设其交点为
相交时,设其交点为 ,当点
,当点 与点
与点 位于直线
位于直线 同侧(不包括点
同侧(不包括点 在直线
在直线 上)时,直接写出
上)时,直接写出 的取值范围.
的取值范围.24.如图,在平面直角坐标系中,抛物线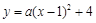 与
与 轴交于
轴交于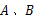 两点,与
两点,与 轴交于点
轴交于点 ,且点
,且点 的坐标为
的坐标为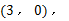 点
点 在这条抛物线上,且不与
在这条抛物线上,且不与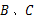 两点重合,过点
两点重合,过点 作
作 轴的垂线与射线
轴的垂线与射线 交于点
交于点 ,以
,以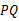 为边作
为边作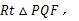 使
使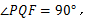 点
点 在点
在点 的下方,且
的下方,且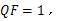 设线段
设线段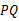 的长度为
的长度为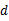 ,点
,点 的横坐标为
的横坐标为 .
.
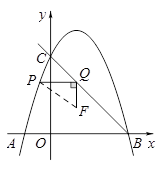
(1)求这条抛物线所对应的函数表达式;
(2)求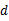 与
与 之间的函数关系式;
之间的函数关系式;
(3)当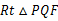 的边
的边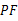 被
被 轴平分时,求
轴平分时,求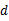 的值;
的值;
(4)以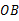 为边作等腰直角三角形
为边作等腰直角三角形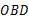 ,当
,当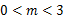 时,直接写出点
时,直接写出点 落在
落在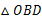 的边上时
的边上时 的值.
的值.
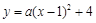 与
与 轴交于
轴交于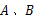 两点,与
两点,与 轴交于点
轴交于点 ,且点
,且点 的坐标为
的坐标为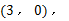 点
点 在这条抛物线上,且不与
在这条抛物线上,且不与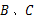 两点重合,过点
两点重合,过点 作
作 轴的垂线与射线
轴的垂线与射线 交于点
交于点 ,以
,以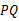 为边作
为边作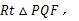 使
使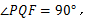 点
点 在点
在点 的下方,且
的下方,且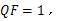 设线段
设线段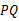 的长度为
的长度为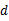 ,点
,点 的横坐标为
的横坐标为 .
.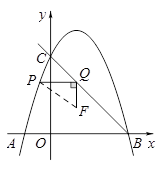
(1)求这条抛物线所对应的函数表达式;
(2)求
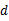 与
与 之间的函数关系式;
之间的函数关系式;(3)当
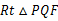 的边
的边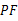 被
被 轴平分时,求
轴平分时,求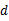 的值;
的值;(4)以
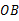 为边作等腰直角三角形
为边作等腰直角三角形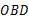 ,当
,当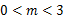 时,直接写出点
时,直接写出点 落在
落在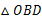 的边上时
的边上时 的值.
的值. 搜索
搜索
 难度系数:0.94
难度系数:0.94  答案解析
答案解析
 有奖纠错
有奖纠错
