搜索
全一卷
难度系数：0.94 
答案解析
有奖纠错
1．
_______ ．
2．计算：
_______ ．
3．化简：
_______ ．
4．分式
在实数范围内有意义，则x的取值范围是______ ．
在实数范围内有意义，则x的取值范围是5．如图，CD是△ABC的中线，点E、F分别是AC、DC的中点，EF=1，则BD=_______ ．
6．如图，直线m∥n，Rt△ABC的顶点A在直线n上，∠C=90°，若∠1=25º，∠2=70º.则∠B= °．
7．一组数据：1，2，1，0，2，a，若它们的众数为1，则这组数据的平均数为_______ ．
8．若关于x的一元二次方程
有两个相等的实数根，则m=_______ ．
有两个相等的实数根，则m=9．已知圆锥的底面半径为3，母线为8，则圆锥的侧面积等于_______ ．
10．如图，将△OAB绕着点O逆时针连续旋转两次得△OA″B″，每次旋转的角度都是50°. 若∠B″OA=120°，则∠AOB的大小为__________ .
11．一辆货车从甲地匀速驶往乙地，到达后用了半小时卸货，随即匀速返回，已知货车返回的速度是它从甲地驶往乙地的速度的1.5倍．货车离甲地的距离y（千米）关于时间x（小时）的函数图象如图所示．则a= （小时）．
12．读取表格中的信息，解决问题.
满足
的n可以取得的最小整数是．
| n=1 |  |  |  |
| n=2 | a2=b1+2c1 | b2=c1+2a1 | c2=a1+2b1 |
| n=3 | a3=b2+2c2 | b3=c2+2a2 | c=a2+2b2 |
| … | … | … | … |
满足
的n可以取得的最小整数是．13．下列运算正确的是（）
A． | B． | C． | D． |
14．一个圆柱如图放置，则它的俯视图是（ ）
| A．三角形 | B．半圆 | C．圆 | D．矩形 |
15．若x、y满足
，则
的值等于（ ）
，则
的值等于（ ）A． | B． | C． | D． |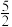
16．如图，△ABC内接于半径为5的⊙O，圆心O到弦BC的距离等于3，则∠A的正切值等于（ ）
A． | B． | C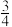． | D． |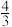
17．已知过点
的直线
不经过第一象限.设
，则s的取值范围是（ ）
的直线不经过第一象限.设，则s的取值范围是（ ）A． | B． | C． | D． |
18．计算：
；
；19．化简：
．
．20．解方程：
21．解不等式：
并将它的解集在数轴上表示出来．
并将它的解集在数轴上表示出来．
22．如图，在四边形ABCD中，AB=AD，BC=DC，AC、BD相交于点O，点E在AO上，且OE=O
| A． （1）求证：∠1=∠2； （2）连结BE、DE，判断四边形BCDE的形状，并说明理由. |
23．为了了解“通话时长”（“通话时长”指每次通话时间）的分布情况，小强收集了他家1000个“通话时长”数据，这些数据均不超过18（分钟）．他从中随机抽取了若干个数据作为样本，统计结果如下表，并绘制了不完整的频数分布直方图．
根据表、图提供的信息，解答下面的问题：
（1）a= ，样本容量是 ；
（2）求样本中“通话时长”不超过9分钟的频率： ；
（3）请估计小强家这1000次通话中“通话时长”超过15分钟的次数．
| “通话时长” （x分钟） | 0＜x≤3 | 3＜x≤6 | 6＜x≤9 | 9＜x≤12 | 12＜x≤15 | 15＜x≤18 |
| 次数 | 36 | a | 8 | 12 | 8 | 12 |
根据表、图提供的信息，解答下面的问题：
（1）a= ，样本容量是 ；
（2）求样本中“通话时长”不超过9分钟的频率： ；
（3）请估计小强家这1000次通话中“通话时长”超过15分钟的次数．
24．在一只不透明的布袋中装有红球、黄球各若干个，这些球除颜色外都相同，均匀摇匀.
（1）若布袋中有3个红球，1个黄球．从布袋中一次摸出2个球，计算“摸出的球恰是一红一黄”的概率（用“画树状图”或“列表”的方法写出计算过程）；
（2）若布袋中有3个红球，x个黄球．
请写出一个x的值 ，使得事件“从布袋中一次摸出4个球，都是黄球”是不可能的事件；
（3）若布袋中有3个红球，4个黄球．
我们知道：“从袋中一次摸出4个球，至少有一个黄球”为必然事件．
请你仿照这个表述，设计一个必然事件： ．
（1）若布袋中有3个红球，1个黄球．从布袋中一次摸出2个球，计算“摸出的球恰是一红一黄”的概率（用“画树状图”或“列表”的方法写出计算过程）；
（2）若布袋中有3个红球，x个黄球．
请写出一个x的值 ，使得事件“从布袋中一次摸出4个球，都是黄球”是不可能的事件；
（3）若布袋中有3个红球，4个黄球．
我们知道：“从袋中一次摸出4个球，至少有一个黄球”为必然事件．
请你仿照这个表述，设计一个必然事件： ．
25．在平面直角坐标系xOy中，直线
与y轴交于点A.
（1）如图，直线
与直线交于点B，与y轴交于点C，点B横坐标为
.
①求点B的坐标及k的值；
②直线与直线
与y轴所围成的△ABC的面积等于 ；
（2）直线与x轴交于点E（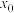
，0），若
，求k的取值范围．
与y轴交于点A.（1）如图，直线
与直线交于点B，与y轴交于点C，点B横坐标为
.①求点B的坐标及k的值；
②直线
与直线
与y轴所围成的△ABC的面积等于 ；（2）直线
与x轴交于点E（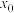
，0），若
，求k的取值范围．
26．如图，小明从点A出发，沿着坡度为为α的斜坡向上走了0.65千米到达点B，sinα=
，然后又沿着坡度为i=1：4的斜坡向上走了1千米达到点C．问小明从A点到点C上升的高度CD是多少千米（结果保留根号）？
，然后又沿着坡度为i=1：4的斜坡向上走了1千米达到点C．问小明从A点到点C上升的高度CD是多少千米（结果保留根号）？27．六•一儿童节，小文到公园游玩．看到公园的一段人行弯道MN（不计宽度），如图，它与两面互相垂直的围墙OP、OQ之间有一块空地MPOQN（MP⊥OP，NQ⊥OQ），他发现弯道MN上任一点到两边围墙的垂线段与围墙所围成的矩形的面积都相等，比如：A、B、C是弯道MN上的三点，矩形ADOG、矩形BEOH、矩形CFOI的面积相等．爱好数学的他建立了平面直角坐标系（如图），图中三块阴影部分的面积分别记为S1、S2、S3，并测得S2=6（单位：平方米）．OG=GH=HI．
（1）求S1和S3的值；
（2）设T（x，y）是弯道MN上的任一点，写出y关于x的函数关系式；
（3）公园准备对区域MPOQN内部进行绿化改造，在横坐标、纵坐标都是偶数的点处种植花木（区域边界上的点除外），已知MP=2米，NQ=3米．问一共能种植多少棵花木？
（1）求S1和S3的值；
（2）设T（x，y）是弯道MN上的任一点，写出y关于x的函数关系式；
（3）公园准备对区域MPOQN内部进行绿化改造，在横坐标、纵坐标都是偶数的点处种植花木（区域边界上的点除外），已知MP=2米，NQ=3米．问一共能种植多少棵花木？
28．如图，已知⊙O的直径AC与弦BD相交于点F，点E是DB延长线上的一点，∠EAB=∠ADB．
（1）求证：AE是⊙O的切线；
（2）已知点B是EF的中点，求证：△EAF∽△CBA；
（3）已知AF=4，CF=2，在（2）的条件下，求AE的长．
（1）求证：AE是⊙O的切线；
（2）已知点B是EF的中点，求证：△EAF∽△CBA；
（3）已知AF=4，CF=2，在（2）的条件下，求AE的长．
29．如图1，在平面直角坐标系xOy中，点M为抛物线
的顶点，过点（0，4）作x轴的平行线，交抛物线于点P、Q（点P在Q的左侧），PQ=4．
（1）求抛物线的函数关系式，并写出点P的坐标；
（2）小丽发现：将抛物线绕着点P旋转180°，所得新抛物线的顶点恰为坐标原点O，你认为正确吗？请说明理由；
（3）如图2，已知点A（1，0），以PA为边作矩形PABC（点P、A、B、C按顺时针的方向排列），
．
①写出C点的坐标：C（ ， ）（坐标用含有t的代数式表示）；
②若点C在题（2）中旋转后的新抛物线上，求t的值．
的顶点，过点（0，4）作x轴的平行线，交抛物线于点P、Q（点P在Q的左侧），PQ=4．（1）求抛物线的函数关系式，并写出点P的坐标；
（2）小丽发现：将抛物线
绕着点P旋转180°，所得新抛物线的顶点恰为坐标原点O，你认为正确吗？请说明理由；（3）如图2，已知点A（1，0），以PA为边作矩形PABC（点P、A、B、C按顺时针的方向排列），
．①写出C点的坐标：C（ ， ）（坐标用含有t的代数式表示）；
②若点C在题（2）中旋转后的新抛物线上，求t的值．
30．我们知道平行四边形有很多性质.
现在如果我们把平行四边形沿着它的一条对角线翻折，会发现这其中还有更多的结论.
（发现与证明）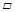
ABCD中，AB≠BC，将△ABC沿AC翻折至△AB′C，连结B′D.
结论1：B′D∥AC；
结论2：△AB′C与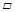ABCD重叠部分的图形是等腰三角形.
……
请利用图1证明结论1或结论2（只需证明一个结论）.
（应用与探究）在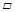ABCD中，已知∠B=30°，将△ABC沿AC翻折至△AB′C，连结B′D.
（1）如图1，若
，则∠ACB= °，BC= ；
（2）如图2，
，BC=1，AB′与边CD相交于点E，求△AEC的面积；
（3）已知，当BC长为多少时，是△AB′D直角三角形？
现在如果我们把平行四边形沿着它的一条对角线翻折，会发现这其中还有更多的结论.
（发现与证明）
ABCD中，AB≠BC，将△ABC沿AC翻折至△AB′C，连结B′D.结论1：B′D∥AC；
结论2：△AB′C与
ABCD重叠部分的图形是等腰三角形.……
请利用图1证明结论1或结论2（只需证明一个结论）.
（应用与探究）在
ABCD中，已知∠B=30°，将△ABC沿AC翻折至△AB′C，连结B′D.（1）如图1，若
，则∠ACB= °，BC= ；（2）如图2，
，BC=1，AB′与边CD相交于点E，求△AEC的面积；（3）已知
，当BC长为多少时，是△AB′D直角三角形？
