搜索
现在如果我们把平行四边形沿着它的一条对角线翻折，会发现这其中还有更多的结论.
（发现与证明）
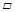ABCD中，AB≠BC，将△ABC沿AC翻折至△AB′C，连结B′D.结论1：B′D∥AC；
结论2：△AB′C与
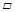ABCD重叠部分的图形是等腰三角形.……
请利用图1证明结论1或结论2（只需证明一个结论）.
（应用与探究）在
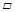ABCD中，已知∠B=30°，将△ABC沿AC翻折至△AB′C，连结B′D.（1）如图1，若
，则∠ACB= °，BC= ；（2）如图2，
，BC=1，AB′与边CD相交于点E，求△AEC的面积；（3）已知
，当BC长为多少时，是△AB′D直角三角形？
同类型试题
y = sin x， x∈R， y∈[–1，1]，周期为2π，函数图像以 x = (π/2) + kπ 为对称轴
y = arcsin x， x∈[–1，1]， y∈[–π/2，π/2]
sin x = 0 ←→ arcsin x = 0
sin x = 1/2 ←→ arcsin x = π/6
sin x = √2/2 ←→ arcsin x = π/4
sin x = 1 ←→ arcsin x = π/2
y = sin x， x∈R， y∈[–1，1]，周期为2π，函数图像以 x = (π/2) + kπ 为对称轴
y = arcsin x， x∈[–1，1]， y∈[–π/2，π/2]
sin x = 0 ←→ arcsin x = 0
sin x = 1/2 ←→ arcsin x = π/6
sin x = √2/2 ←→ arcsin x = π/4
sin x = 1 ←→ arcsin x = π/2
