搜索
（1）求下面各比的比值。
6∶9＝ 2.8∶4＝
∶
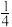＝ 3∶5＝
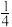∶ ＝ 1.4∶2＝ 0.9∶1.2＝ 9∶15＝（2）提示：如果两个比的比值相等，这两个比可以组成比例。找出上面可以组成比例的比并写出来。
（3）在比例3∶5＝9∶15中，3×（ ）＝5×（ ），这时我们可以说，在比例中，内项的积等于外项的积，这个性质是比例的基本性质。
利用比例的基本性质，可以把比例中的未知项求出来。
如：解比例：6∶x＝2∶7
解：2x＝6×7－－－（在比例中，两个内项的积等于两个外项的积）
2x÷2＝6×7÷2－－－（等式的两边同时除以2）
x＝21
我也模仿着解比例：4∶x＝3∶21。
同类型试题
y = sin x， x∈R， y∈[–1，1]，周期为2π，函数图像以 x = (π/2) + kπ 为对称轴
y = arcsin x， x∈[–1，1]， y∈[–π/2，π/2]
sin x = 0 ←→ arcsin x = 0
sin x = 1/2 ←→ arcsin x = π/6
sin x = √2/2 ←→ arcsin x = π/4
sin x = 1 ←→ arcsin x = π/2
y = sin x， x∈R， y∈[–1，1]，周期为2π，函数图像以 x = (π/2) + kπ 为对称轴
y = arcsin x， x∈[–1，1]， y∈[–π/2，π/2]
sin x = 0 ←→ arcsin x = 0
sin x = 1/2 ←→ arcsin x = π/6
sin x = √2/2 ←→ arcsin x = π/4
sin x = 1 ←→ arcsin x = π/2
