小明:如图1,(1)分别在射线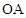 , , 上截取 上截取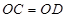 , , (点 (点 , , 不重合);(2)分别作线段 不重合);(2)分别作线段 , ,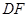 的垂直平分线 的垂直平分线 , ,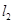 ,交点为 ,交点为 ,垂足分别为点 ,垂足分别为点 , ,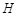 ;(3)作射线 ;(3)作射线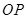 ,射线 ,射线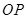 即为 即为 的平分线.简述理由如下: 的平分线.简述理由如下:由作图,  , , , , ,所以 ,所以 ,则 ,则 ,即射线 ,即射线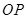 是 是 的平分线. 的平分线.小军:我认为小明的作图方法很有创意,但是大麻烦了,可以改进如下,如图2.(1)分别在射线 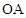 , , 上截取 上截取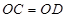 , , (点 (点 , , 不重合);(2)连接 不重合);(2)连接 , , ,交点为 ,交点为 ;(3)作射线 ;(3)作射线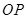 ,射线 ,射线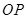 即为 即为 的平分线. 的平分线.……  |
(1)小明得出
 的依据是 .(填序号)
的依据是 .(填序号)①
 ;②
;② ;③
;③ ;④
;④ ;⑤
;⑤ .
.(2)小军作图得到的射线
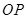 是
是 的平分线吗?请判断并说明理由;
的平分线吗?请判断并说明理由;(3)如图3,已知
 ,点
,点 ,
, 分别在射线
分别在射线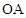 ,
, 上,且
上,且 .点
.点 ,
, 分别为射线
分别为射线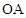 ,
, 上的动点,且
上的动点,且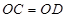 ,连接
,连接 ,
, ,交点为
,交点为 ,当
,当 时,直接写出线段
时,直接写出线段 的长.
的长.

同类型试题

y = sin x, x∈R, y∈[–1,1],周期为2π,函数图像以 x = (π/2) + kπ 为对称轴
y = arcsin x, x∈[–1,1], y∈[–π/2,π/2]
sin x = 0 ←→ arcsin x = 0
sin x = 1/2 ←→ arcsin x = π/6
sin x = √2/2 ←→ arcsin x = π/4
sin x = 1 ←→ arcsin x = π/2
y = sin x, x∈R, y∈[–1,1],周期为2π,函数图像以 x = (π/2) + kπ 为对称轴
y = arcsin x, x∈[–1,1], y∈[–π/2,π/2]
sin x = 0 ←→ arcsin x = 0
sin x = 1/2 ←→ arcsin x = π/6
sin x = √2/2 ←→ arcsin x = π/4
sin x = 1 ←→ arcsin x = π/2
 搜索
搜索

