搜索
．（1）求证：四边形ABCD是正方形；
（2）若H是AB上的一点（H与A，B不重合），连接DH，将线段DH绕点H顺时针旋转90度，得到线段HE，过点E分别作BC及AB的延长线的垂线，垂足分别是F，G，设四边形BGEF的面积为
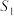，以HB，BC为邻边的矩形面积为
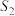，且
，当
时，求AH的长；
同类型试题
y = sin x， x∈R， y∈[–1，1]，周期为2π，函数图像以 x = (π/2) + kπ 为对称轴
y = arcsin x， x∈[–1，1]， y∈[–π/2，π/2]
sin x = 0 ←→ arcsin x = 0
sin x = 1/2 ←→ arcsin x = π/6
sin x = √2/2 ←→ arcsin x = π/4
sin x = 1 ←→ arcsin x = π/2
y = sin x， x∈R， y∈[–1，1]，周期为2π，函数图像以 x = (π/2) + kπ 为对称轴
y = arcsin x， x∈[–1，1]， y∈[–π/2，π/2]
sin x = 0 ←→ arcsin x = 0
sin x = 1/2 ←→ arcsin x = π/6
sin x = √2/2 ←→ arcsin x = π/4
sin x = 1 ←→ arcsin x = π/2
