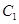搜索
的函数解析式为y=ax2+bx-3a(b<0)，若抛物线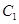经过点（0，-3），方程ax2+bx-3a=0的两根为x1，x2，且
.（1）求抛物线
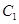的顶点坐标；（2）已知实数
，请证明：
≥
,并说明
为何值时才会有
；（3）若抛物线先向上平移4个单位，再向左平移1个单位后得到抛物线
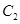，设A（m，y1）)B（n，y2）是C2上两个不同点，且满足
，m>0，n<0. 用含有
的表达式表示出△
的面积
，并求出的最小值及取最小值时一次函数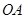
的函数解析式．（参考公式：在平面直角坐标系中，若
，
，则
，
两点间的距离为
）
同类型试题
y = sin x， x∈R， y∈[–1，1]，周期为2π，函数图像以 x = (π/2) + kπ 为对称轴
y = arcsin x， x∈[–1，1]， y∈[–π/2，π/2]
sin x = 0 ←→ arcsin x = 0
sin x = 1/2 ←→ arcsin x = π/6
sin x = √2/2 ←→ arcsin x = π/4
sin x = 1 ←→ arcsin x = π/2
y = sin x， x∈R， y∈[–1，1]，周期为2π，函数图像以 x = (π/2) + kπ 为对称轴
y = arcsin x， x∈[–1，1]， y∈[–π/2，π/2]
sin x = 0 ←→ arcsin x = 0
sin x = 1/2 ←→ arcsin x = π/6
sin x = √2/2 ←→ arcsin x = π/4
sin x = 1 ←→ arcsin x = π/2
