搜索
(1)温故：如图 1，在△ABC中，AD⊥BC 于点D，正方形PQMN 的边QM在BC上，顶点P ，N 分别在AB， AC上，若BC=6 ，AD=4，求正方形 PQMN的边长．
(2)操作：能画出这类正方形吗?小波按数学家波利亚在《怎样解题》中的方法进行操作：如图 2，任意画△ABC，在AB上任取一点P′，画正方形 P′Q′M′N′ ，使Q′,M′在BC边上， N′在△ABC 内，连结B N′ 并延长交AC 于点N，画NM⊥BC于点M，NP⊥NM 交AB于点P，PQ⊥BC 于点Q，得到四边形 PQMN．小波把线段BN 称为“波利亚线”．
(3)推理：证明图2 中的四边形 PQMN 是正方形．
(4)拓展：在(2)的条件下，于波利业线B N 上截取NE=NM ，连结EQ ，EM(如图 3)．当tan∠NBM=
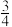时，猜想∠QEM的度数，并尝试证明．请帮助小波解决“温故”、“推理”、“拓展”中的问题．
同类型试题
y = sin x， x∈R， y∈[–1，1]，周期为2π，函数图像以 x = (π/2) + kπ 为对称轴
y = arcsin x， x∈[–1，1]， y∈[–π/2，π/2]
sin x = 0 ←→ arcsin x = 0
sin x = 1/2 ←→ arcsin x = π/6
sin x = √2/2 ←→ arcsin x = π/4
sin x = 1 ←→ arcsin x = π/2
y = sin x， x∈R， y∈[–1，1]，周期为2π，函数图像以 x = (π/2) + kπ 为对称轴
y = arcsin x， x∈[–1，1]， y∈[–π/2，π/2]
sin x = 0 ←→ arcsin x = 0
sin x = 1/2 ←→ arcsin x = π/6
sin x = √2/2 ←→ arcsin x = π/4
sin x = 1 ←→ arcsin x = π/2
