搜索
如图1，在平面之间坐标系xOy中，A，B两点的坐标分别为A（x1，y1），B（x2，y2），由勾股定理得AB2=|x2﹣x1|2+|y2﹣y1|2，所以A，B两点间的距离为
．我们知道，圆可以看成到圆心距离等于半径的点的集合，如图2，在平面直角坐标系xoy中，A（x，y）为圆上任意一点，则A到原点的距离的平方为OA2=|x﹣0|2+|y﹣0|2，当⊙O的半径为r时，⊙O的方程可写为：x2+y2=r2．
问题拓展：如果圆心坐标为P（a，b），半径为r，那么⊙P的方程可以写为 ．
综合应用：
如图3，⊙P与x轴相切于原点O，P点坐标为（0，6），A是⊙P上一点，连接OA，使tan∠POA=
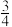，作PD⊥OA，垂足为D，延长PD交x轴于点B，连接AB．①证明AB是⊙P的切线；
②是否存在到四点O，P，A，B距离都相等的点Q？若存在，求Q点坐标，并写出以Q为圆心，以OQ为半径的⊙O的方程；若不存在，说明理由．
同类型试题
y = sin x， x∈R， y∈[–1，1]，周期为2π，函数图像以 x = (π/2) + kπ 为对称轴
y = arcsin x， x∈[–1，1]， y∈[–π/2，π/2]
sin x = 0 ←→ arcsin x = 0
sin x = 1/2 ←→ arcsin x = π/6
sin x = √2/2 ←→ arcsin x = π/4
sin x = 1 ←→ arcsin x = π/2
y = sin x， x∈R， y∈[–1，1]，周期为2π，函数图像以 x = (π/2) + kπ 为对称轴
y = arcsin x， x∈[–1，1]， y∈[–π/2，π/2]
sin x = 0 ←→ arcsin x = 0
sin x = 1/2 ←→ arcsin x = π/6
sin x = √2/2 ←→ arcsin x = π/4
sin x = 1 ←→ arcsin x = π/2
