搜索
全一卷
难度系数：0.64 
答案解析
有奖纠错
1．
的和是奇数还是偶数？
的和是奇数还是偶数？ 2． 
得数是奇数还是偶数？
得数是奇数还是偶数？ 3． 
得数是奇数还是偶数？
得数是奇数还是偶数？ 4．
的计算结果是奇数还是偶数，为什么？
的计算结果是奇数还是偶数，为什么？5．
的和是奇数还是偶数？为什么？
的和是奇数还是偶数？为什么？ 6．东东在做算术题时，写出了如下一个等式：
，他做得对吗？
，他做得对吗？ 7．能否在下式的“□”内填入加号或减号，使等式成立，若能请填入符号，不能请说明理由
（1）1 □ 2 □ 3 □ 4 □ 5 □ 6 □ 7 □ 8 □ 9＝10
（2）1 □ 2 □ 3 □ 4 □ 5 □ 6 □ 7 □ 8 □ 9＝27
（1）1 □ 2 □ 3 □ 4 □ 5 □ 6 □ 7 □ 8 □ 9＝10
（2）1 □ 2 □ 3 □ 4 □ 5 □ 6 □ 7 □ 8 □ 9＝27
8． 能否从四个3，三个5，两个7中选出5个数，使这5个数的和等于22.
9．能否从、四个6，三个10，两个14中选出5个数，使这5个数的和等于44.
10．一个自然数数分别与另外两个相邻奇数相乘，所得的两个积相差150，那么这个数是多少？
11．一个偶数分别与其相邻的两个偶数相乘，所得的两个乘积相差80，那么这三个偶数的和是多少？
12．多米诺骨牌是由塑料制成的1×2长方形，共28张，每张牌上的两个1×1正方形中刻有“点”，点的个数分别为0，1，2，…，6个不等，其中7张牌两端的点数一样，即两个0，两个1，…，两个6；其余21张牌两端的点数不一样，所谓连牌规则是指：每相邻两张牌必须有一端的点数相同，且以点数相同的端相连，例如：
现将一付多米诺骨牌按连牌规则连成一条链，如果在链的一端为6点，那么在链的另一端为多少点?并简述你的理由．
现将一付多米诺骨牌按连牌规则连成一条链，如果在链的一端为6点，那么在链的另一端为多少点?并简述你的理由．
13． 一条线段上分布着n个点，这些点的颜色不是黑的就是白的，它们将线段分为n+1段，已知线段两端的两个点都是黑的，而中间的每一个点的两边各有一黑一白.那么白点的数目是奇数还是偶数？
14．是否存在自然数a和b，使得ab(a＋b)="115?"
15． 是否存在自然数a、b、c，使得(a-b)(b-c)(a-c)=45327？
16．a、b、c三个数的和与它们的积的和为奇数，问这三个数中最多可以有几个奇数？
17．已知a,b,c中有一个是511，一个是622，一个是793。求证：
是一个偶数
是一个偶数18．小红写了四个不同的非零整数a,b,c,d，并且说这四个整数满足四个算式：
但是小明看过之后立刻说小红是错的，根不不存在这样的四个数，你能证明小明的结论吗？
但是小明看过之后立刻说小红是错的，根不不存在这样的四个数，你能证明小明的结论吗？
19．设
, 
, 
, 
, 
, 
, 
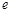都是整数，试说明：
在
中，必有奇数个偶数．
, 
, 
, 
, 
, 
, 
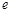都是整数，试说明：在
中，必有奇数个偶数．20．有四个互不相等的自然数，最大数与最小数的差等于4，最小数与最大数的乘积是一个奇数，而这四个数的和是最小的两位奇数。求这四个数。
21．甲、乙两个哲人将正整数5至11分别写在7张卡片上．他们将卡片背面朝上，任意混合之后，甲取走三张，乙取走两张．剩下的两张卡片，他们谁也没看，就放到麻袋里去了．甲认真研究了自己手中的三张卡片之后，对乙说：“我知道你的两张卡片上的数的和是偶数．”试问：甲手中的三张卡片上都写了哪些数？答案是否唯一．
22．甲同学一手握有写着23的纸片，另一只手握有写着32的纸片．乙同学请甲回答如下一个问题：“请将左手中的数乘以3，右手中的数乘以2，再将这两个积相加，这个和是奇数还是偶数？”当甲说出和为奇数时，乙马上就猜出写有23的纸片握在甲的左手中．你能说出是什么道理吗？
23．在一张
行列的方格纸上，把每个方格所在的行数和列数加起来，填在这个方格中，例如
．问：填入的
个数字中是奇数多还是偶数多？
行列的方格纸上，把每个方格所在的行数和列数加起来，填在这个方格中，例如
．问：填入的
个数字中是奇数多还是偶数多？ 
24．如果把每个方格所在的行数和列数乘起来，填在这个方格，例如：a=5×3=15．问填入的81个数中是奇数多还是偶数多？
25．试找出两个整数，使大数与小数之和加上大数与小数之差，再加上
等于
。如果找得出来，请写出这两个数，如果找不出来，请说明理由。
等于
。如果找得出来，请写出这两个数，如果找不出来，请说明理由。26． 你能不能将自然数1到9分别填入3×3的方格表中，使得每一行中的三个数之和都是偶数
27．你能不能将整数数0到8分别填入3×3的方格表中，使得每一行中的三个数之和都是奇数?
28．任意交换某个三位数的数字顺序，得到一个新的三位数，原三位数与新三位数之和能否等于999？
29．两个四位数相加，第一个四位数每个数码都小于5，第二个四位数仅仅是第一个四位数的四个数码调换了位置，两个数的和可能是7356吗？为什么？
30．有一串数，最前面的四个数依次是1、9、8、7。从第五个数起，每一个数都是它前面相邻四个数之和的各位数字，那么在这一串数中，会依次出现1、9、8、8这四个数吗？
31．数列
，，
，
，
，
，
，
，
，
，
的排列规律是前两个数是，从第三个数开始，每一个数都是它前两个数的和，这个数列叫做斐波那契数列，在斐波那契数列前
个数中共有几个偶数？
，，
，
，
，
，
，
，
，
，
的排列规律是前两个数是，从第三个数开始，每一个数都是它前两个数的和，这个数列叫做斐波那契数列，在斐波那契数列前
个数中共有几个偶数？ 32． 黑板上写着两个数1和2，按下列规则增写新数，若黑板有两个数a和b，则增写a×b＋a＋b这个数，比如可增写5（因为1×2＋1＋2＝5）增写11（因为1×5＋1＋5＝11），一直写下去，问能否得到2008，若不能，说明理由，若能则说出最少需要写几次得到？
33． 在一次聚会时，朋友们陆续到来，见面时，有些人互相握手问好．主人很高兴，笑着说：“不论你们怎样握手，你们之中，握过奇数次手的人必定有偶数个．”请你想一想，主人为什么这么说，他有什么理由呢？
34．元旦前夕，同学们相互送贺年卡．每人只要接到对方贺年卡就一定回赠贺年卡，那么送了奇数张贺年卡的人数是奇数，还是偶数？为什么？
35．桌子上有6只开口向上的杯子，每次同时翻动其中的5只杯子，问能否经过若干次翻动，使得全部杯子的开口全都向下？
36．桌子上有5个开口向上的杯子，现在允许每次同时翻动其中的4个，问能否经过若干次翻动，使得5个杯子的开口全都向下？
37．桌子上有6只开口向上的杯子，每次同时翻动其中的4只杯子，问能否经过若干次翻动，使得全部杯子的开口全都向下？
38．在8个房间中，有7个房间开着灯，1个房间关着灯。如果每次拨动4个不同房间的开关，能不能把全部房间的灯都关上？为什么？
39．沿着河岸长着8丛植物，相邻两丛植物上所结的浆果数目相差1个。问：8丛植物上能否一共结有225个浆果？说明理由。
40．四个人一道去郊游，他们年龄的和是97岁，最小的一人只有10岁，他与年龄最大的人的岁数和比另外两人岁数的和大7岁．问：⑴ 年龄最大的人是多少岁？⑵ 另外两人的岁数的奇偶性相同吗？
41．在“
”的方格中放棋子，每格至多放1枚棋子．若要求行、列、
条斜线（如图所示）上的棋子数均为偶数．那么“”的方格中最多可以放多少枚棋子？ 
”的方格中放棋子，每格至多放1枚棋子．若要求行、列、
条斜线（如图所示）上的棋子数均为偶数．那么“”的方格中最多可以放多少枚棋子？ 
42．有8个棱长是1的小正方体，每个小正方体有三组相对的面，第一组相对的面上都写着数字1，第二组相对的面上都写着数字2，第三组相对的面上都写着数字3(如图)．现在把这8个小正方体拼成一个棱长是2的大正方体.。问：是否有一种拼合方式，使得大正方体每一个面上的4个数字之和恰好组成6个连续的自然数?
43．圆桌旁坐着2k个人，其中有k个物理学家和k个化学家，并且其中有些人总说真话，有些人则总说假话．今知物理学家中说假话的人同化学家中说假话的人一样多．又当问及：“你的右邻是什么人”时，大家全部回答：“是化学家．”那么请你证明：k为偶数．
44．有一个袋子里边装着红、黄、蓝三种颜色的球，现在小峰每次从口袋中取出3个球，如果发现三个球中有两个球的颜色相同，就将第三个球放还回口袋，如果三个球的颜色各不相同，就往口袋中放一个黄球，已知原来有红球42个、黄球23个、蓝球43，那么取到不能再取的时候，口袋里还有蓝球，那么蓝球有多少个？
45． 一个图书馆分东西两个阅览室．东阅览室里每张桌子上有2盏灯．西阅览室里每张桌子上有3盏灯．现在知道两个阅览室里的总的桌子数和灯数都是奇数．问：哪个阅览室的桌子数是奇数？
46．四年级一班同学参加学校的数学竞赛，试题共50道，评分标准是：答对一道给3分，不答给1分，答错倒扣1分．请你说明：该班同学的得分总和一定是偶数．
47．师傅与徒弟加工同一种零件，各人把产品放在自己的箩筐里，师傅的产量是徒弟的2倍，师傅的产品放在4只箩筐中，徒弟的产品放在2只箩筐中，每只箩筐都标明了产品的只数：78只，94只，86只，87只，82只，80只．根据上面的条件，你能找出哪两只筐的产品是徒弟制造的吗？
48．在黑板上写出三个整数，然后擦去一个换成其它两数之和，这样继续操作下去，最后得到66，88，237．问：原来写的三个整数能否为1，3，5？
49． 苹果，梨，橘子三种水果都有许多，混在一起合成一大堆．最少要分成多少堆(每堆都有苹果，梨子和橘子三种水果)才能保证找到这样的两堆，把这两堆合并后这三种水果的个数都是偶数？
50．有一批文章共15篇，各篇文章的页数是1页、2页、3页、
、14页和15页的稿纸，如果将这些文章按某种次序装订成册，并统一编上页码，那么每篇文章的第一页是奇数页码的文章最多有多少篇？
、14页和15页的稿纸，如果将这些文章按某种次序装订成册，并统一编上页码，那么每篇文章的第一页是奇数页码的文章最多有多少篇？ 51．有一个袋子里装着许多玻璃球．这些玻璃球或者是黑色的，或者是白色的．假设有人从袋中取球，每次取两只球．如果取出的两只球是同色的，那么，他就往袋里放回一只白球；如果取出的两只球是异色的，那么，他就往袋里放回一只黑球．他这样取了若干次以后，最后袋子里只剩下一只黑球．请问：原来在这个袋子里有奇数个还是偶数个黑球？
52．有大、小两个盒子，其中大盒内装1001枚白棋和1000枚同样大小的黑棋子，小盒内装有足够多的黑棋．康康每次从大盒内随意摸出两枚棋子：若摸出的两枚棋子同色，则从小盒内取一枚黑子放入大盒内；若摸出的两枚棋子异色，则把其中白棋子放回大盒内．问：从大盒内摸了1999次棋子后，大盒内还剩几枚棋子？它们都是什么颜色？
