全一卷
1.函数 的反函数
的反函数 =
=_________ .
 的反函数
的反函数 =
=2.若复数z满足方程 (i是虚数单位),则
(i是虚数单位),则
_____________ .
 (i是虚数单位),则
(i是虚数单位),则
3.函数 的最小正周期为
的最小正周期为_____________ .
 的最小正周期为
的最小正周期为4.在 的展开式中,常数项为
的展开式中,常数项为_____ .
 的展开式中,常数项为
的展开式中,常数项为5.若双曲线的一个顶点坐标为 ,焦距为
,焦距为 ,则它的标准方程为
,则它的标准方程为________ .
 ,焦距为
,焦距为 ,则它的标准方程为
,则它的标准方程为6.圆心在直线y=x上且与x轴相切于点 的圆的方程是
的圆的方程是______ .
 的圆的方程是
的圆的方程是7.计算:
_____________ .

8.若向量 满足
满足 ,则
,则 与
与 所成角的大小为
所成角的大小为_____________ .
 满足
满足 ,则
,则 与
与 所成角的大小为
所成角的大小为9.袋内装有大小相同的6个球,2个是红球,4个是白球,若从中任意取出3个球,则所取出的3个球中至少有1个红球的概率是_____ .
10.若记号“*”表示求两个实数a与b的算术平均的运算,即 ,则两边均含有运算“*”和“+”,且对任意3个实数a,b,c都能成立的一个等式可以是
,则两边均含有运算“*”和“+”,且对任意3个实数a,b,c都能成立的一个等式可以是____ .
 ,则两边均含有运算“*”和“+”,且对任意3个实数a,b,c都能成立的一个等式可以是
,则两边均含有运算“*”和“+”,且对任意3个实数a,b,c都能成立的一个等式可以是11.甲、乙两人于同一天分别携款1万元到银行储蓄,甲存五年期定期储蓄,年利率为2.88%.乙存一年期定期储蓄,年利率为2.25%,并在每年到期时将本息续存一年期定期储蓄.按规定每次计息时,储户须交纳利息的20%作为利息税,若存满五年后两人同时从银行取出存款,则甲与乙所得本息之和的差为_____________ 元.(假定利率五年内保持不变,结果精确到1分)
12.关于 的函数
的函数 有以下命题:(1)对任意的
有以下命题:(1)对任意的 都是非奇非偶函数;(2)不存在
都是非奇非偶函数;(2)不存在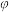 ,使
,使 既是奇函数,又是偶函数;(3)存在
既是奇函数,又是偶函数;(3)存在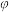 ,使
,使 是奇函数;(4)对任意的
是奇函数;(4)对任意的 都不是偶函数,其中一个假命题的序号是
都不是偶函数,其中一个假命题的序号是_____ ,因为当
_____ 时,该命题的结论不成立.
 的函数
的函数 有以下命题:(1)对任意的
有以下命题:(1)对任意的 都是非奇非偶函数;(2)不存在
都是非奇非偶函数;(2)不存在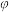 ,使
,使 既是奇函数,又是偶函数;(3)存在
既是奇函数,又是偶函数;(3)存在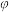 ,使
,使 是奇函数;(4)对任意的
是奇函数;(4)对任意的 都不是偶函数,其中一个假命题的序号是
都不是偶函数,其中一个假命题的序号是
13.“ ”是 “
”是 “ ”的
”的
 ”是 “
”是 “ ”的
”的 | A.充分不必要条件 |
| B.必要不充分条件 |
| C.充要条件 |
| D.既不充分也不必要条件 |
14.若直线 的倾斜角为
的倾斜角为 ,则
,则
 的倾斜角为
的倾斜角为 ,则
,则
A.等于 | B.等于 | C.等于 | D.不存在 |
15.若有平面 与
与 ,且
,且 ,则下列命题中的假命题为( )
,则下列命题中的假命题为( )
 与
与 ,且
,且 ,则下列命题中的假命题为( )
,则下列命题中的假命题为( )A.过点P且垂直于 的直线平行于 的直线平行于 | B.过点P且垂直于l的平面垂直于 |
C.过点P且垂直于 的直线在 的直线在 内 内 | D.过点P且垂直于l的直线在 内 内 |
16.若数列{an}前8项的值各异,且an+8=an对任意n∈N*都成立,则下列数列中可取遍{an}前8项值的数列为 ( )
| A.{a2k+1} | B.{a3k+1} | C.{a4k+1} | D.{a6k+1} |
17.已知R为全集, ,求
,求 .
.
 ,求
,求 .
.18.已知 试用
试用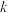 表示
表示 的值.
的值.
 试用
试用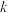 表示
表示 的值.
的值.19.用一块钢锭烧铸一个厚度均匀,且表面积为2m2的正四棱锥形有盖容器(如下图).设容器高为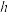 m,盖子边长为
m,盖子边长为 m,
m,

(1)求 关于
关于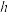 的解析式;
的解析式;
(2)设容器的容积为V m3,则当h为何值时,V最大? 并求出V的最大值(求解本题时,不计容器厚度).
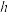 m,盖子边长为
m,盖子边长为 m,
m,
(1)求
 关于
关于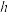 的解析式;
的解析式;(2)设容器的容积为V m3,则当h为何值时,V最大? 并求出V的最大值(求解本题时,不计容器厚度).
20.在长方体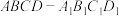 中,点E、F分别
中,点E、F分别 上,且
上,且 .
.

(1)求证: 平面
平面 ;
;
(2)若规定两个平面所成的角是这两个平面所组成的二面角中的锐角(或直角),则在空间中有定理:若两条直线分别垂直于两个平面,则这两条直线所成的角与这两个平面所成的角相等.试根据上述定理,在 时,求平面
时,求平面 与平面
与平面 所成的角的大小.(用反三角函数值表示)
所成的角的大小.(用反三角函数值表示)
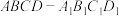 中,点E、F分别
中,点E、F分别 上,且
上,且 .
.
(1)求证:
 平面
平面 ;
;(2)若规定两个平面所成的角是这两个平面所组成的二面角中的锐角(或直角),则在空间中有定理:若两条直线分别垂直于两个平面,则这两条直线所成的角与这两个平面所成的角相等.试根据上述定理,在
 时,求平面
时,求平面 与平面
与平面 所成的角的大小.(用反三角函数值表示)
所成的角的大小.(用反三角函数值表示)21.已知椭圆C的方程为 ,点P(a,b)的坐标满足
,点P(a,b)的坐标满足 ,过点P的直线l与椭圆交于A、B两点,点Q为线段AB的中点,求:
,过点P的直线l与椭圆交于A、B两点,点Q为线段AB的中点,求:
(1)点Q的轨迹方程;
(2)点Q的轨迹与坐标轴的交点的个数.
 ,点P(a,b)的坐标满足
,点P(a,b)的坐标满足 ,过点P的直线l与椭圆交于A、B两点,点Q为线段AB的中点,求:
,过点P的直线l与椭圆交于A、B两点,点Q为线段AB的中点,求:(1)点Q的轨迹方程;
(2)点Q的轨迹与坐标轴的交点的个数.
22.已知数列 是首项为2,公比为
是首项为2,公比为 的等比数列,且前
的等比数列,且前 项和为
项和为 .
.
(1)用 表示
表示 ;
;
(2)是否存在自然数 和
和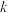 ,使得
,使得 成立?
成立?
 是首项为2,公比为
是首项为2,公比为 的等比数列,且前
的等比数列,且前 项和为
项和为 .
.(1)用
 表示
表示 ;
;(2)是否存在自然数
 和
和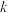 ,使得
,使得 成立?
成立? 搜索
搜索
 难度系数:0.85
难度系数:0.85  答案解析
答案解析
 有奖纠错
有奖纠错
