全一卷
1.复数 的值是( )
的值是( )
 的值是( )
的值是( )A. | B.1 | C. | D.32 |
2. ( )
( )
 ( )
( )A. | B. | C. | D. |
3.命题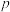 :若
:若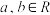 ,则
,则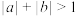 是
是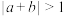 的充要条件;命题
的充要条件;命题 :函数
:函数 的定义域是
的定义域是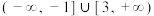 ,则( )
,则( )
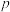 :若
:若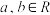 ,则
,则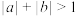 是
是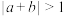 的充要条件;命题
的充要条件;命题 :函数
:函数 的定义域是
的定义域是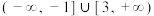 ,则( )
,则( )A.“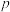 或 或 ”为假 ”为假 | B.“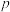 且 且 ”为真 ”为真 | C.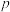 真 真 假 假 | D.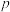 假 假 真 真 |
4.已知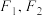 是椭圆的两个焦点,过
是椭圆的两个焦点,过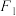 且与椭圆长轴垂直的直线交椭圆于
且与椭圆长轴垂直的直线交椭圆于 两点,若
两点,若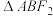 是正三角形,则这个椭圆的离心率是( )
是正三角形,则这个椭圆的离心率是( )
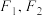 是椭圆的两个焦点,过
是椭圆的两个焦点,过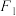 且与椭圆长轴垂直的直线交椭圆于
且与椭圆长轴垂直的直线交椭圆于 两点,若
两点,若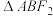 是正三角形,则这个椭圆的离心率是( )
是正三角形,则这个椭圆的离心率是( )A. | B. | C.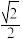 | D. |
5.已知m、n是不重合的直线,α、β是不重合的平面,有下列命题:①若m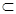 α,n∥α,则m∥n;②若m∥α,m∥β,则α∥β;③若α∩β=n,m∥n,则m∥α且m∥β;④若m⊥α,m⊥β,则α∥β.其中真命题的个数是( )
α,n∥α,则m∥n;②若m∥α,m∥β,则α∥β;③若α∩β=n,m∥n,则m∥α且m∥β;④若m⊥α,m⊥β,则α∥β.其中真命题的个数是( )
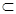 α,n∥α,则m∥n;②若m∥α,m∥β,则α∥β;③若α∩β=n,m∥n,则m∥α且m∥β;④若m⊥α,m⊥β,则α∥β.其中真命题的个数是( )
α,n∥α,则m∥n;②若m∥α,m∥β,则α∥β;③若α∩β=n,m∥n,则m∥α且m∥β;④若m⊥α,m⊥β,则α∥β.其中真命题的个数是( )| A.0 | B.1 | C.2 | D.3 |
6.某校高二年级共有六个班,现从外地转入 名学生,要安排到该年级的两个班级且每班安排
名学生,要安排到该年级的两个班级且每班安排 名,则不同的安排方案种数为( )
名,则不同的安排方案种数为( )
 名学生,要安排到该年级的两个班级且每班安排
名学生,要安排到该年级的两个班级且每班安排 名,则不同的安排方案种数为( )
名,则不同的安排方案种数为( )A. | B. | C. | D. |
7.已知函数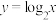 的反函数是
的反函数是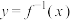 ,则函数
,则函数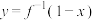 的图像是( ).
的图像是( ).
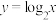 的反函数是
的反函数是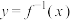 ,则函数
,则函数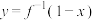 的图像是( ).
的图像是( ).A. | B. |
C. | D. |
8.已知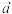 ,
, 是非零向量且满足
是非零向量且满足 ,
,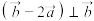 ,则
,则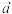 与
与 的夹角是( )
的夹角是( )
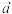 ,
, 是非零向量且满足
是非零向量且满足 ,
,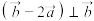 ,则
,则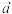 与
与 的夹角是( )
的夹角是( )A. | B. | C. | D. |
9.若 展开式的第3项为288,则
展开式的第3项为288,则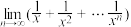 的值是( )
的值是( )
 展开式的第3项为288,则
展开式的第3项为288,则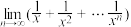 的值是( )
的值是( )| A.2 | B.1 | C. | D.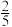 |
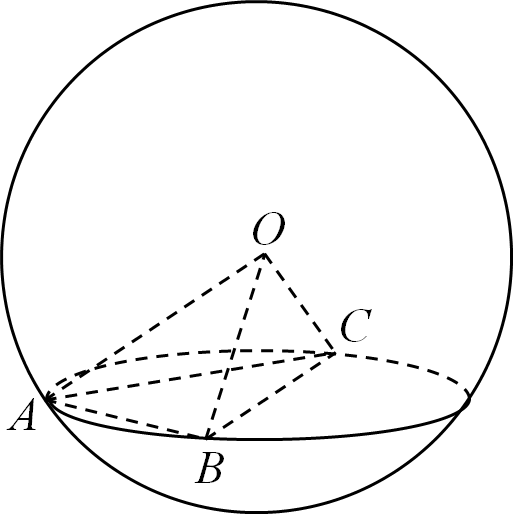
10.如图,A、B、C是表面积为 的球面上三点,
的球面上三点,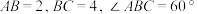 ,O为球心,则直线
,O为球心,则直线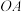 与截面
与截面 所成的角是( )
所成的角是( )
 的球面上三点,
的球面上三点,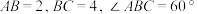 ,O为球心,则直线
,O为球心,则直线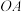 与截面
与截面 所成的角是( )
所成的角是( )
A. | B. | C. | D. |
11.定义在R上的函数f(x)满足f(x)=f(x+2),当x∈[3,5]时,f(x)=2﹣|x﹣4|,
A. | B. |
C. | D. |
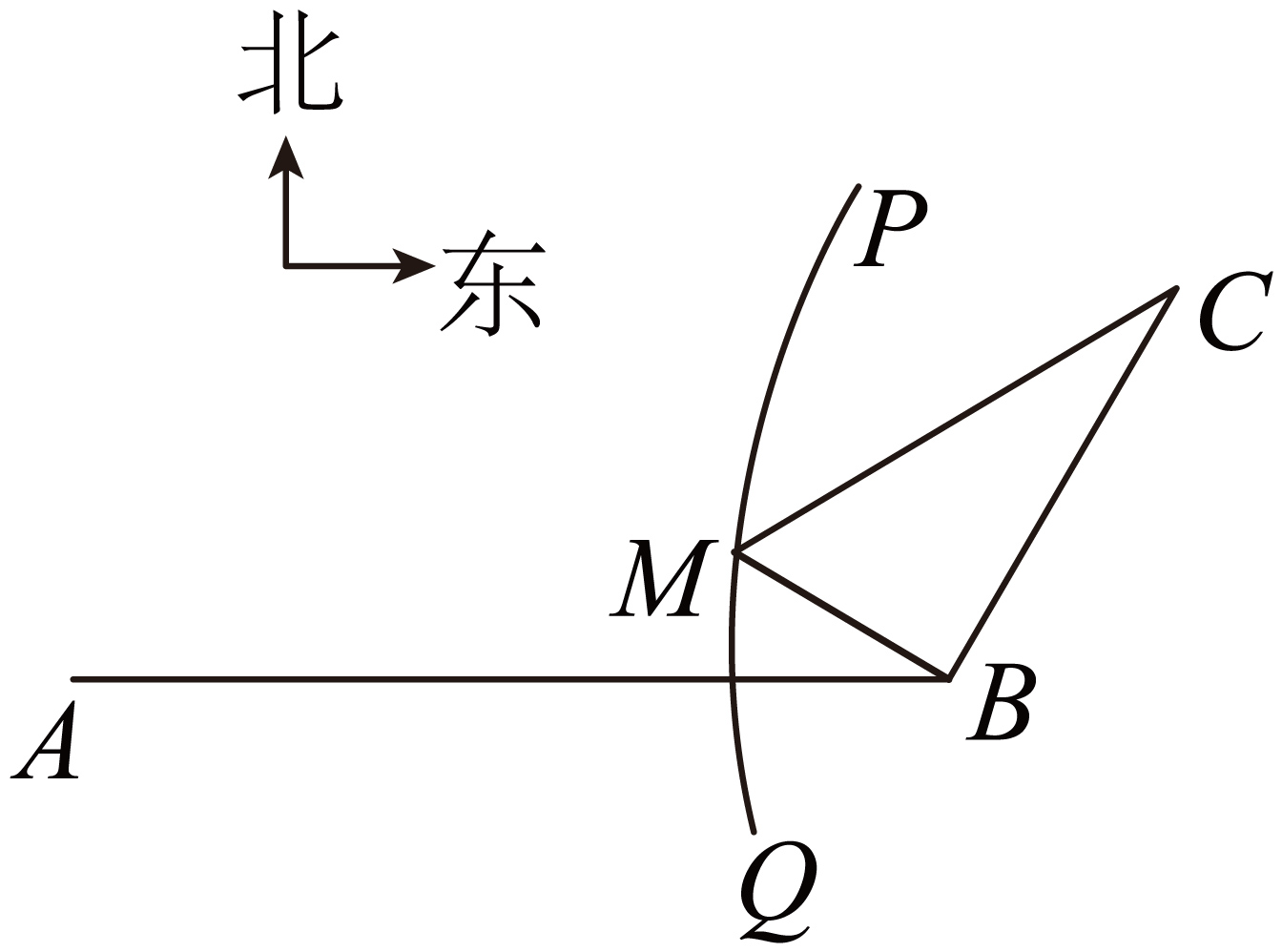
12.如图, 地在
地在 地的正东方向
地的正东方向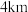 处,
处, 地在
地在 地的北偏东
地的北偏东 方向
方向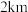 处,河流的沿岸
处,河流的沿岸 (曲线)上任意一点到
(曲线)上任意一点到 的距离比到
的距离比到 的距离远
的距离远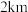 .现要在曲线
.现要在曲线 上一处
上一处 建一座码头,向
建一座码头,向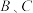 两地转运货物.经测算,从
两地转运货物.经测算,从 到
到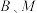 到
到 修建公路的费用分别是
修建公路的费用分别是 万元
万元 、
、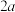 万元
万元 ,那么修建这两条公路的总费用最低是( )
,那么修建这两条公路的总费用最低是( )
 地在
地在 地的正东方向
地的正东方向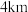 处,
处, 地在
地在 地的北偏东
地的北偏东 方向
方向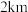 处,河流的沿岸
处,河流的沿岸 (曲线)上任意一点到
(曲线)上任意一点到 的距离比到
的距离比到 的距离远
的距离远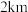 .现要在曲线
.现要在曲线 上一处
上一处 建一座码头,向
建一座码头,向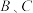 两地转运货物.经测算,从
两地转运货物.经测算,从 到
到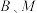 到
到 修建公路的费用分别是
修建公路的费用分别是 万元
万元 、
、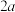 万元
万元 ,那么修建这两条公路的总费用最低是( )
,那么修建这两条公路的总费用最低是( )
A. 万元 万元 | B. 万元 万元 | C. 万元 万元 | D. 万元 万元 |
13.直线x+2y=0被曲线x2+y2﹣6x﹣2y﹣15=0所截得的弦长等于 .
14.设函数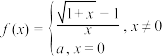 在
在 处连续,则实数a的值为
处连续,则实数a的值为_____________ .
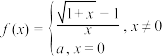 在
在 处连续,则实数a的值为
处连续,则实数a的值为15.某射手射击1次,击中目标的概率是0.9,他连续射击4次,且他各次射击是否击中目标相互之间没有影响.有下列结论:
①他第3次击中目标的概率是0.9;
②他恰好击中目标3次的概率是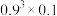 ;
;
③他至少击中目标1次的概率是 .
.
其中正确结论的序号是____ .(写出所有正确结论的序号)
①他第3次击中目标的概率是0.9;
②他恰好击中目标3次的概率是
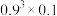 ;
;③他至少击中目标1次的概率是
 .
.其中正确结论的序号是
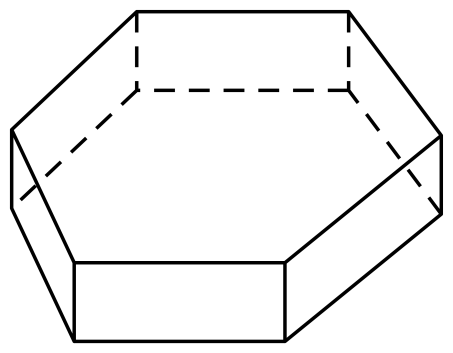
16.如图,将边长为1的正六边形铁皮的六个角各切去一个全等的四边形,再沿虚线折起,做成一个无盖的正六棱柱容器(图).当这个正六棱柱容器的底面边长为 时,其容积最大. 


17.设函数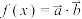 ,其中向量
,其中向量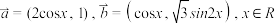 .
.
(1)若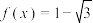 且
且 ,求
,求 ;
;
(2)若函数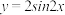 的图象按向量
的图象按向量 =平移后得到函数
=平移后得到函数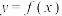 的图象,求实数
的图象,求实数 的值.
的值.
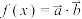 ,其中向量
,其中向量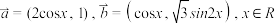 .
.(1)若
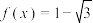 且
且 ,求
,求 ;
;(2)若函数
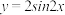 的图象按向量
的图象按向量 =平移后得到函数
=平移后得到函数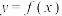 的图象,求实数
的图象,求实数 的值.
的值.18.甲、乙两人同时参加奥运志愿者的选拔赛,已知在备选的10道题中,甲能答对其中的6题,乙能答对其中的8题,规定每次考试都从备选题中随机抽出3题进行测试,至少答对2题才能入选.
(1)求甲答对试题数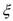 的分布列及数学期望;
的分布列及数学期望;
(2)求甲、乙两人至少有一人入选的概率.
(1)求甲答对试题数
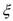 的分布列及数学期望;
的分布列及数学期望;(2)求甲、乙两人至少有一人入选的概率.
19.在三棱锥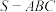 中,
中, 是边长为4的正三角形,平面
是边长为4的正三角形,平面 平面
平面 ,
,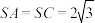 ,M、N分别为
,M、N分别为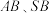 的中点.
的中点.
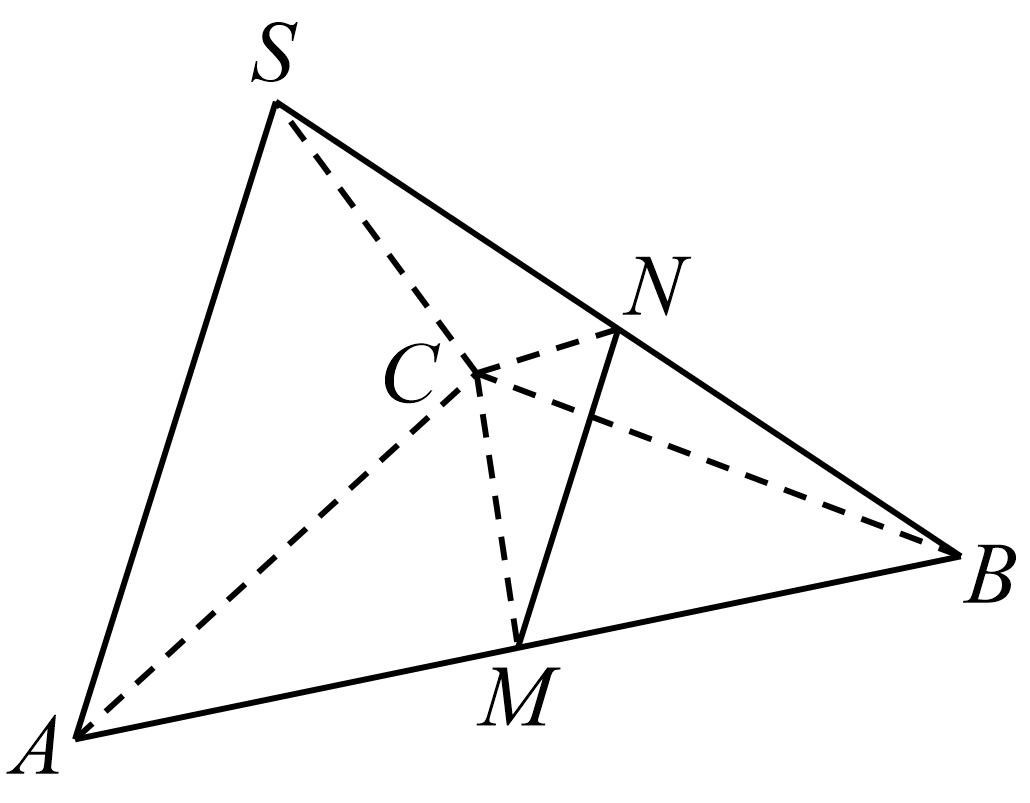
(1)证明: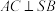 ;
;
(2)求二面角 的大小;
的大小;
(3)求点B到平面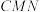 的距离.
的距离.
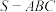 中,
中, 是边长为4的正三角形,平面
是边长为4的正三角形,平面 平面
平面 ,
,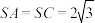 ,M、N分别为
,M、N分别为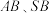 的中点.
的中点.
(1)证明:
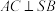 ;
;(2)求二面角
 的大小;
的大小;(3)求点B到平面
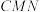 的距离.
的距离.20.某企业去年的纯利润为500万元,因设备老化,企业的生产能力逐渐下降.若不进行技术改造,预测从今年起每年的纯利润比上一年减少20万元.今年年初该企业一次性投入600万元资金进行技术改造,预测在未扣除技术改造资金的情况下,第n年(今年为第一年)的利润为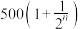 万元(n为正整数).
万元(n为正整数).
(1)设从今年起的前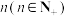 年,若该企业不进行技术改造的累计纯利润为
年,若该企业不进行技术改造的累计纯利润为 万元,进行技术改造的累计纯利润为
万元,进行技术改造的累计纯利润为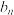 万元(扣除技术改造资金),求
万元(扣除技术改造资金),求 ,
,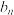 的表达式;
的表达式;
(2)依上述预测,从今年起该企业至少经过多少年,进行技术改造后的累计纯利润将超过不进行技术改造的累计纯利润.
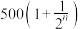 万元(n为正整数).
万元(n为正整数).(1)设从今年起的前
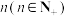 年,若该企业不进行技术改造的累计纯利润为
年,若该企业不进行技术改造的累计纯利润为 万元,进行技术改造的累计纯利润为
万元,进行技术改造的累计纯利润为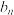 万元(扣除技术改造资金),求
万元(扣除技术改造资金),求 ,
,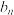 的表达式;
的表达式;(2)依上述预测,从今年起该企业至少经过多少年,进行技术改造后的累计纯利润将超过不进行技术改造的累计纯利润.
21.已知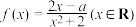 在区间
在区间 上是增函数.
上是增函数.
(1)求实数a的值组成的集合A;
(2)设关于x的方程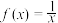 的两个非零实根为
的两个非零实根为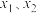 .试问:是否存在实数m,使得不等式
.试问:是否存在实数m,使得不等式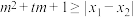 对任意
对任意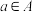 及
及 恒成立?若存在,求m的取值范围;若不存在,请说明理由.
恒成立?若存在,求m的取值范围;若不存在,请说明理由.
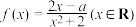 在区间
在区间 上是增函数.
上是增函数.(1)求实数a的值组成的集合A;
(2)设关于x的方程
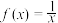 的两个非零实根为
的两个非零实根为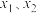 .试问:是否存在实数m,使得不等式
.试问:是否存在实数m,使得不等式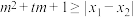 对任意
对任意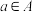 及
及 恒成立?若存在,求m的取值范围;若不存在,请说明理由.
恒成立?若存在,求m的取值范围;若不存在,请说明理由.22.如图,P是抛物线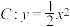 上一点,直线l过点P且与抛物线C交于另一点Q.
上一点,直线l过点P且与抛物线C交于另一点Q.

(1)若直线l与过点P的切线垂直,求线段PQ中点M的轨迹方程;
(2)若直线l不过原点且与x轴交于点S,与y轴交于点T,试求 的取值范围.
的取值范围.
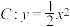 上一点,直线l过点P且与抛物线C交于另一点Q.
上一点,直线l过点P且与抛物线C交于另一点Q.
(1)若直线l与过点P的切线垂直,求线段PQ中点M的轨迹方程;
(2)若直线l不过原点且与x轴交于点S,与y轴交于点T,试求
 的取值范围.
的取值范围. 搜索
搜索
 难度系数:0.85
难度系数:0.85  答案解析
答案解析
 有奖纠错
有奖纠错
