全一卷
1.已知全集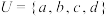 ,集合
,集合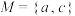 ,则
,则 等于( )
等于( )
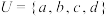 ,集合
,集合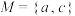 ,则
,则 等于( )
等于( )A. | B. | C. | D. |
2.函数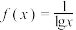 的定义域是( )
的定义域是( )
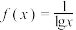 的定义域是( )
的定义域是( )A. | B. | C. | D. |
3.已知函数 的定义域是
的定义域是 ,若对于任意两个不相等的实数
,若对于任意两个不相等的实数 ,
, ,总有
,总有 成立,则函数
成立,则函数 一定是( )
一定是( )
 的定义域是
的定义域是 ,若对于任意两个不相等的实数
,若对于任意两个不相等的实数 ,
, ,总有
,总有 成立,则函数
成立,则函数 一定是( )
一定是( )| A.奇函数 | B.偶函数 | C.增函数 | D.减函数 |
4.已知平行四边形 ,点
,点 ,
, 分别是
分别是 ,
, 的中点(如图所示),设
的中点(如图所示),设 ,
, ,则
,则 等于( )
等于( )

 ,点
,点 ,
, 分别是
分别是 ,
, 的中点(如图所示),设
的中点(如图所示),设 ,
, ,则
,则 等于( )
等于( )
A. | B. | C. | D. |
5.在等比数列 中,
中, ,
, ,则
,则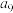 等于( )
等于( )
 中,
中, ,
, ,则
,则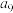 等于( )
等于( )| A.256 | B.-256 | C.512 | D.-512 |
6.已知直线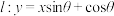 的图像如图所示,则角
的图像如图所示,则角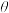 是( )
是( )
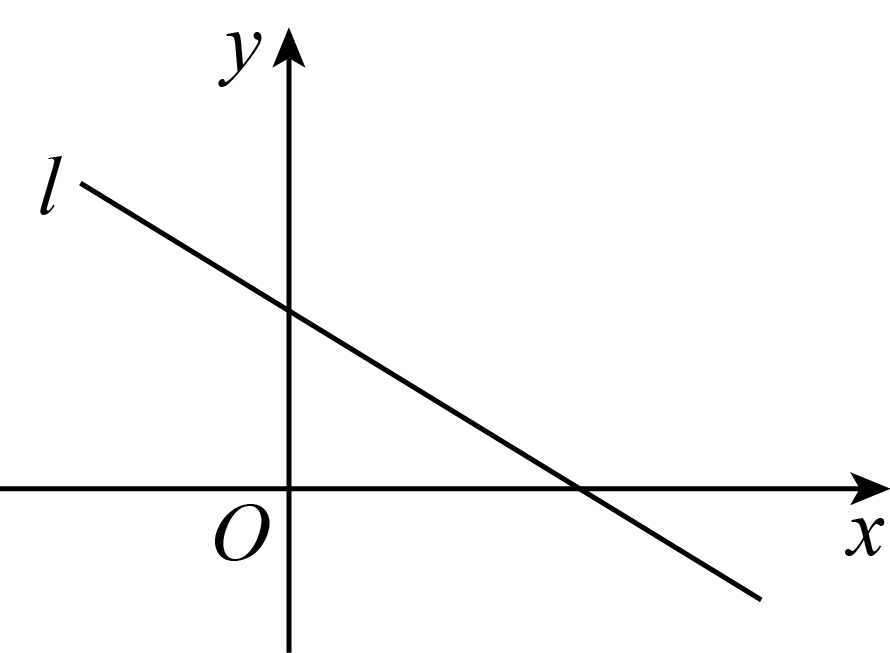
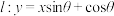 的图像如图所示,则角
的图像如图所示,则角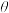 是( )
是( )
| A.第一象限角 | B.第二象限角 | C.第三象限角 | D.第四象限角 |
7.已知圆心为 的圆与
的圆与 轴相切,则该圆的标准方程是( )
轴相切,则该圆的标准方程是( )
 的圆与
的圆与 轴相切,则该圆的标准方程是( )
轴相切,则该圆的标准方程是( )A. | B. |
C. | D. |
8.现从4名男生和3名女生中,任选3名男生和2名女生,分别担任5门不同学科的课代表,则不同安排方法的种数是( )
| A.12 | B.120 | C.1440 | D.17280 |
9.在 的二项展开式中,第
的二项展开式中,第 项的二项式系数是( )
项的二项式系数是( )
 的二项展开式中,第
的二项展开式中,第 项的二项式系数是( )
项的二项式系数是( )A. | B. | C. | D. |
10.直线 关于点
关于点 对称的直线方程是( )
对称的直线方程是( )
 关于点
关于点 对称的直线方程是( )
对称的直线方程是( )A. | B. |
C. | D. |
11.已知 ,若集合
,若集合 ,
, ,则“
,则“ ”是“
”是“ ”的( )
”的( )
 ,若集合
,若集合 ,
, ,则“
,则“ ”是“
”是“ ”的( )
”的( )| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
12.已知二次函数 的图像如图所示,则不等式
的图像如图所示,则不等式 的解集是( )
的解集是( )

 的图像如图所示,则不等式
的图像如图所示,则不等式 的解集是( )
的解集是( )
A. | B. | C. | D. |
13.已知函数 是偶函数,当
是偶函数,当 时,
时, ,则该函数在
,则该函数在 上的图像大致是( )
上的图像大致是( )
 是偶函数,当
是偶函数,当 时,
时, ,则该函数在
,则该函数在 上的图像大致是( )
上的图像大致是( )A. | B. |
C. | D. |
14.下列命题为真命题的是( )
A. 且 且 | B. 或 或 |
C. , , | D. , , |
15.已知点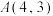 ,
,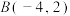 ,点
,点 在函数
在函数 图象的对称轴上,若
图象的对称轴上,若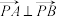 ,则点
,则点 的坐标是( )
的坐标是( )
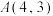 ,
,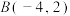 ,点
,点 在函数
在函数 图象的对称轴上,若
图象的对称轴上,若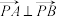 ,则点
,则点 的坐标是( )
的坐标是( )A. 或 或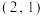 | B. 或 或 |
C. 或 或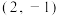 | D. 或 或 |
16.现有5位老师,若每人随机进入两间教室中的任意一间听课,则恰好全都进入同一间教室的概率是( )
A. | B. | C. | D. |
17.已知椭圆的长轴长为10,焦距为8,则该椭圆的短轴长等于( )
| A.3 | B.6 | C.8 | D.12 |
18.已知变量 ,
, 满足某约束条件,其可行域(阴影部分)如图所示,则目标函数
满足某约束条件,其可行域(阴影部分)如图所示,则目标函数 的取值范围是( )
的取值范围是( )

 ,
, 满足某约束条件,其可行域(阴影部分)如图所示,则目标函数
满足某约束条件,其可行域(阴影部分)如图所示,则目标函数 的取值范围是( )
的取值范围是( )
A. | B. | C. | D. |
19.已知正方体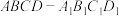 (如图所示),则下列结论正确的是( )
(如图所示),则下列结论正确的是( )
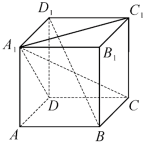
 (如图所示),则下列结论正确的是( )
(如图所示),则下列结论正确的是( )
A. | B. | C. | D. |
20.在 中,内角
中,内角 ,
, ,
, 的对边分别是
的对边分别是 ,
, ,
, ,若
,若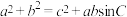 ,且
,且
 ,则
,则 等于( )
等于( )
 中,内角
中,内角 ,
, ,
, 的对边分别是
的对边分别是 ,
, ,
, ,若
,若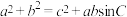 ,且
,且
 ,则
,则 等于( )
等于( )| A.3 | B. | C.3或 | D.-3或 |
21.已知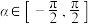 ,若
,若 ,则
,则
______ 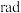 .
.
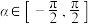 ,若
,若 ,则
,则
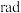 .
.22.若 ,则实数
,则实数 的值是
的值是______ .
 ,则实数
,则实数 的值是
的值是23.已知球的直径为2,则该球的体积是______ .
24.某创新企业为了解新研发的一种产品的销售情况,从编号为001,002,…480的480个专卖店销售数据中,采用系统抽样的方法抽取一个样本,若样本中的个体编号依次为005,021,…则样本中的最后一个个体编号是______ .
25.已知抛物线的顶点在坐标原点,焦点 与双曲线
与双曲线 的左焦点重合,若两曲线相交于
的左焦点重合,若两曲线相交于 ,
, 两点,且线段
两点,且线段 的中点是点
的中点是点 ,则该双曲线的离心率等于
,则该双曲线的离心率等于______ .
 与双曲线
与双曲线 的左焦点重合,若两曲线相交于
的左焦点重合,若两曲线相交于 ,
, 两点,且线段
两点,且线段 的中点是点
的中点是点 ,则该双曲线的离心率等于
,则该双曲线的离心率等于26.已知函数 .
.
(1)求 的值;
的值;
(2)求 ,求实数
,求实数 的取值范围.
的取值范围.
 .
.(1)求
 的值;
的值;(2)求
 ,求实数
,求实数 的取值范围.
的取值范围.27.某男子擅长走路,9天共走了1260里,其中第1天、第4天、第7天所走的路程之和为390里.若从第2天起,每天比前一天多走的路程相同,问该男子第5天走多少里.这是我国古代数学专著《九章算术》中的一个问题,请尝试解决.
28.小明同学用“五点法”作某个正弦型函数 在一个周期内的图象时,列表如下:
在一个周期内的图象时,列表如下:
根据表中数据,求:
(1)实数 ,
, ,
, 的值;
的值;
(2)该函数在区间 上的最大值和最小值.
上的最大值和最小值.
 在一个周期内的图象时,列表如下:
在一个周期内的图象时,列表如下: |  |  |  |  |  |
 | 0 |  |  |  |  |
 | 0 | 3 | 0 | -3 | 0 |
(1)实数
 ,
, ,
, 的值;
的值;(2)该函数在区间
 上的最大值和最小值.
上的最大值和最小值.29.已知点 ,
, 分别是正方形
分别是正方形 的边
的边 ,
, 的中点.现将四边形
的中点.现将四边形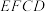 沿
沿 折起,使二面角
折起,使二面角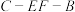 为直二面角,如图所示.
为直二面角,如图所示.

(1)若点 ,
, 分别是
分别是 ,
,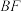 的中点,求证:
的中点,求证: 平面
平面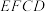 ;
;
(2)求直线 与平面
与平面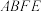 所成角的正弦值.
所成角的正弦值.
 ,
, 分别是正方形
分别是正方形 的边
的边 ,
, 的中点.现将四边形
的中点.现将四边形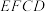 沿
沿 折起,使二面角
折起,使二面角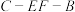 为直二面角,如图所示.
为直二面角,如图所示.
(1)若点
 ,
, 分别是
分别是 ,
,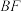 的中点,求证:
的中点,求证: 平面
平面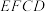 ;
;(2)求直线
 与平面
与平面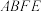 所成角的正弦值.
所成角的正弦值.30.已知抛物线的顶点在坐标原点 ,椭圆
,椭圆 的顶点分别为
的顶点分别为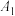 ,
, ,
,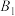 ,
,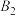 ,其中点
,其中点 为抛物线的焦点,如图所示.
为抛物线的焦点,如图所示.
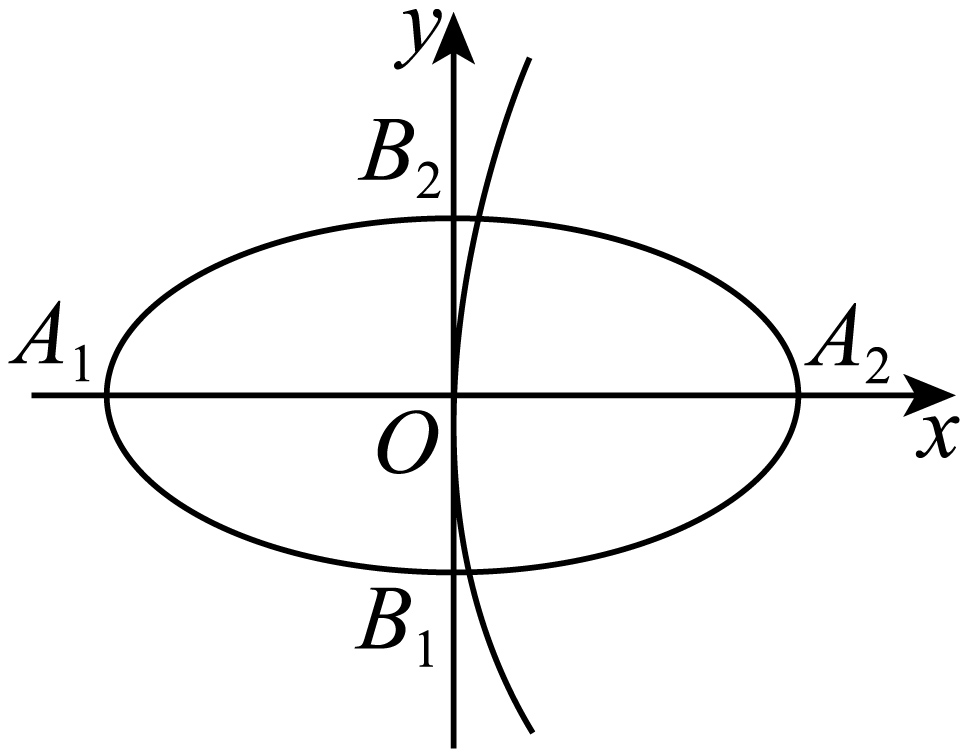
(1)求抛物线的标准方程;
(2)若过点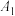 的直线
的直线 与抛物线交于
与抛物线交于 ,
, 两点,且
两点,且 ,求直线
,求直线 的方程.
的方程.
 ,椭圆
,椭圆 的顶点分别为
的顶点分别为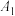 ,
, ,
,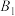 ,
,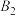 ,其中点
,其中点 为抛物线的焦点,如图所示.
为抛物线的焦点,如图所示.
(1)求抛物线的标准方程;
(2)若过点
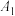 的直线
的直线 与抛物线交于
与抛物线交于 ,
, 两点,且
两点,且 ,求直线
,求直线 的方程.
的方程. 搜索
搜索
 难度系数:0.85
难度系数:0.85  答案解析
答案解析
 有奖纠错
有奖纠错
