全一卷
1.已知集合 ,
, ,若
,若 ,则
,则 的值是( )
的值是( )
 ,
, ,若
,若 ,则
,则 的值是( )
的值是( )| A.-2 | B.-1 | C.0 | D.1 |
2.若数组 和
和 满足
满足 ,则实数
,则实数 等于( )
等于( )
 和
和 满足
满足 ,则实数
,则实数 等于( )
等于( )| A.-3 | B.-2 | C. | D. |
3.若复数 满足
满足 ,则
,则 的虚部等于( )
的虚部等于( )
 满足
满足 ,则
,则 的虚部等于( )
的虚部等于( )| A.4 | B.2 | C.-2 | D.-4 |
4.逻辑表达式 等于( )
等于( )
 等于( )
等于( )A. | B. | C. | D. |
5.已知 的展开式中
的展开式中 的系数为40,则
的系数为40,则 等于( )
等于( )
 的展开式中
的展开式中 的系数为40,则
的系数为40,则 等于( )
等于( )| A.5 | B.6 | C.7 | D.8 |
6.已知双曲线 的一条渐近线与直线
的一条渐近线与直线 平行,则该双曲线的离心率是( )
平行,则该双曲线的离心率是( )
 的一条渐近线与直线
的一条渐近线与直线 平行,则该双曲线的离心率是( )
平行,则该双曲线的离心率是( )A. | B. | C.2 | D. |
7.若圆锥的轴截面为等腰直角三角形,则它的底面积与侧面积之比是( )
A. | B. | C. | D. |
8.下图是某项工程的网络图(单位:天),则从开始节点①到终止节点⑧的路径共有( )


| A.14条 | B.12条 | C.9条 | D.7条 |
9.若函数 的最小正周期为
的最小正周期为 ,则它的一条对称轴是( )
,则它的一条对称轴是( )
 的最小正周期为
的最小正周期为 ,则它的一条对称轴是( )
,则它的一条对称轴是( )A. | B. |
C. | D. |
10.已知奇函数 是定义在
是定义在 上的单调函数,若正实数
上的单调函数,若正实数 ,
, 满足
满足 则
则 的最小值是( )
的最小值是( )
 是定义在
是定义在 上的单调函数,若正实数
上的单调函数,若正实数 ,
, 满足
满足 则
则 的最小值是( )
的最小值是( )A. | B. | C.2 | D.4 |
11.下图是一个程序框图,执行该程序框图,则输出的n值是___________ .


12.已知等比数列 的公比为
的公比为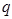 ,且
,且 ,
, ,
,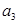 成等差数列,则
成等差数列,则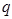 的值是
的值是___________ .
 的公比为
的公比为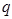 ,且
,且 ,
, ,
,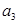 成等差数列,则
成等差数列,则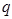 的值是
的值是13.已知 ,且
,且 ,则
,则 的值是
的值是_________ .
 ,且
,且 ,则
,则 的值是
的值是14.以抛物线 的焦点为圆心,且与直线
的焦点为圆心,且与直线 (
( 为参数)相切的圆的标准方程是
为参数)相切的圆的标准方程是____________ .
 的焦点为圆心,且与直线
的焦点为圆心,且与直线 (
( 为参数)相切的圆的标准方程是
为参数)相切的圆的标准方程是15.已知函数 ,若其图像上存在互异的三个点
,若其图像上存在互异的三个点 ,
, ,
, ,使得
,使得 ,则实数
,则实数 的取值范围是
的取值范围是__________ .
 ,若其图像上存在互异的三个点
,若其图像上存在互异的三个点 ,
, ,
, ,使得
,使得 ,则实数
,则实数 的取值范围是
的取值范围是16.已知函数 的定义域是
的定义域是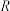 .
.
(1)求实数 的取值范围;
的取值范围;
(2)解关于 的不等式
的不等式 .
.
 的定义域是
的定义域是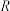 .
.(1)求实数
 的取值范围;
的取值范围;(2)解关于
 的不等式
的不等式 .
.17.已知函数 是定义在
是定义在 上的偶函数,当
上的偶函数,当 时,
时, (
( ,且
,且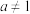 ).又直线
).又直线 恒过定点A,且点A在函数
恒过定点A,且点A在函数 的图像上.
的图像上.
(1) 求实数 的值;
的值;
(2) 求 的值;
的值;
(3) 求函数 的解析式.
的解析式.
 是定义在
是定义在 上的偶函数,当
上的偶函数,当 时,
时, (
( ,且
,且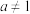 ).又直线
).又直线 恒过定点A,且点A在函数
恒过定点A,且点A在函数 的图像上.
的图像上.(1) 求实数
 的值;
的值;(2) 求
 的值;
的值;(3) 求函数
 的解析式.
的解析式.18.已知关于 的二次函数
的二次函数 .
.
(1)若 ,
, ,求事件
,求事件 在
在 上是增函数}的概率;
上是增函数}的概率;
(2)若 ,
, ,求事件
,求事件 “方程
“方程 没有实数根”的概率.
没有实数根”的概率.
 的二次函数
的二次函数 .
.(1)若
 ,
, ,求事件
,求事件 在
在 上是增函数}的概率;
上是增函数}的概率;(2)若
 ,
, ,求事件
,求事件 “方程
“方程 没有实数根”的概率.
没有实数根”的概率.19.已知向量 ,
, ,设函数
,设函数 .
.
(1)求函数 的最大值;
的最大值;
(2)在锐角 中,三个角
中,三个角 ,
, ,
, 所对的边分别为
所对的边分别为 ,
, ,
, ,若
,若 ,
, ,求
,求 的面积.
的面积.
 ,
, ,设函数
,设函数 .
.(1)求函数
 的最大值;
的最大值;(2)在锐角
 中,三个角
中,三个角 ,
, ,
, 所对的边分别为
所对的边分别为 ,
, ,
, ,若
,若 ,
, ,求
,求 的面积.
的面积.20.某化工厂引进一条先进生产线生产某种化工产品,其生产的总成本 万元与年产量
万元与年产量 吨之间的函数关系可以近似地表示为
吨之间的函数关系可以近似地表示为 ,已知此生产线的年产量最小为60吨,最大为110吨.
,已知此生产线的年产量最小为60吨,最大为110吨.
(1)年产量为多少吨时,生产每吨产品的平均成本最低?并求最低平均成本;
(2)若每吨产品的平均出厂价为24万元,且产品能全部售出,则年产量为多少吨时,可以获得最大利润?并求最大利润.
 万元与年产量
万元与年产量 吨之间的函数关系可以近似地表示为
吨之间的函数关系可以近似地表示为 ,已知此生产线的年产量最小为60吨,最大为110吨.
,已知此生产线的年产量最小为60吨,最大为110吨.(1)年产量为多少吨时,生产每吨产品的平均成本最低?并求最低平均成本;
(2)若每吨产品的平均出厂价为24万元,且产品能全部售出,则年产量为多少吨时,可以获得最大利润?并求最大利润.
21.已知数列 满足
满足 ,且
,且 .
.
(1)求证:数列 为等比数列;
为等比数列;
(2)求数列 的通项公式;
的通项公式;
(3)求数列 的前
的前 项和
项和 .
.
 满足
满足 ,且
,且 .
.(1)求证:数列
 为等比数列;
为等比数列;(2)求数列
 的通项公式;
的通项公式;(3)求数列
 的前
的前 项和
项和 .
.22.某广告公司接到幸福社区制作疫情防控宣传标牌的任务,要制作文字标牌4个,绘画标牌5个,该公司现有两种规格的原料,甲种规格原料每张3m2,可做文字标牌1个和绘画标牌2个;乙种规格原料每张2m2,可做文字标牌2个和绘画标牌1个.问两种规格的原料各用多少张时,才能使总的用料面积最小?并求最小用料面积.
23.已知椭圆 的离心率为
的离心率为 .
.
(1)证明: ;
;
(2)若点 在椭圆
在椭圆 的内部,过点
的内部,过点 的直线
的直线 交椭圆
交椭圆 于
于 、
、 两点,
两点, 为线段
为线段 的中点,且
的中点,且 .
.
①求直线 的方程;
的方程;
②求椭圆 的标准方程.
的标准方程.
 的离心率为
的离心率为 .
.(1)证明:
 ;
;(2)若点
 在椭圆
在椭圆 的内部,过点
的内部,过点 的直线
的直线 交椭圆
交椭圆 于
于 、
、 两点,
两点, 为线段
为线段 的中点,且
的中点,且 .
.①求直线
 的方程;
的方程;②求椭圆
 的标准方程.
的标准方程. 搜索
搜索
 难度系数:0.94
难度系数:0.94  答案解析
答案解析
 有奖纠错
有奖纠错
