搜索
全一卷
难度系数：0.65 
答案解析
有奖纠错
1．设
，则
的大小顺序是（ ）.
，则
的大小顺序是（ ）.A． . |
B． . |
C． . |
D． . |
2．设
是定义在实数集上的周期为2的周期函数，且是偶函数.已知当
时，
；则当
时的解析式是（ ）.
是定义在实数集上的周期为2的周期函数，且是偶函数.已知当
时，
；则当
时的解析式是（ ）.A． . | B． . |
C． . | D． . |
3．设双曲线的左右焦点是
，左右顶点是M,N.若
的顶点P在双曲线上，则的内切圆与边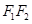
的切点位置是（ ）.
，左右顶点是M,N.若
的顶点P在双曲线上，则的内切圆与边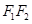
的切点位置是（ ）.| A．在线段MN内部. | B．在线段 内部或线段 内部. |
| C．点M或点N. | D．不能确定. |
4．点集
中元素的个数为（ ）.
中元素的个数为（ ）.| A．0. | B．1. | C．2. | D．多于2. |
5．设非零复数
满足
，则代数式
的值是（ ）.
满足
，则代数式
的值是（ ）.A． . | B．-1. | C．1. | D．以上答案都不对. |
6．设n为自然数，a，b为正实数，且满足
，则
的最小值是______________.
，则
的最小值是______________.7．设A（2，0）为平面上一定点，
为动点，则当t由15°变到45°时，线段AP所扫过的图形的面积是______________.
为动点，则当t由15°变到45°时，线段AP所扫过的图形的面积是______________.8．设n为自然数，对于任意实数
，恒有
成立，则n的最小值是_____________.
，恒有
成立，则n的最小值是_____________.9．在坐标平面上，横坐标和纵坐标均为整数的点称为整点.对任意自然数n，连接原点O与点
，用
表示线段
上除端点外的整点的个数，则
________________.
，用
表示线段
上除端点外的整点的个数，则
________________.10．8个女孩和25个男孩围成一圈，任何两个女孩之间至少站两个男孩，则共有__________________种不同的排列方法.（只要把圈旋转一下就重合的排法认为是相同的）.
11．已知
均为正整数，且
，
（其中
），
.求证对一切自然数n，
均为整数.
均为正整数，且
，
（其中
），
.求证对一切自然数n，
均为整数.12．
个正数排列n行n列：
其中每一行的数成等差数列，每一列的数成等比数列，并且所有公比相等.已知
，求
.
个正数排列n行n列：
其中每一行的数成等差数列，每一列的数成等比数列，并且所有公比相等.已知
，求
.13．设棱锥M-ABCD的底面是正方形，且MA=MD，MA⊥A
| A．如果△AMD的面积为1，试求能够放入这个棱锥的最大球的半径. |
