全一卷
1.定义: .若
.若 .
.  ,则
,则 等于.
等于.
 .若
.若 .
.  ,则
,则 等于.
等于.A. | B. | C. | D. |
2.函数 的部分图像是图的().
的部分图像是图的().
 的部分图像是图的().
的部分图像是图的().A. | B. |
C. | D. |
3.若不等式 对所有正实数
对所有正实数  、
、 都成立,则
都成立,则 的最小值是.
的最小值是.
 对所有正实数
对所有正实数  、
、 都成立,则
都成立,则 的最小值是.
的最小值是.| A.2 | B. | C. | D.4 |
4.曲线 和
和 的交点有个.
的交点有个.
 和
和 的交点有个.
的交点有个.| A.2 | B.3 | C.4 | D.无穷多 |
5.设 .若
.若  ,则数列
,则数列  .
.
 .若
.若  ,则数列
,则数列  .
.| A.递增 | B.奇数项增,偶数项减 |
| C.递减 | D.偶数项增,奇数项减 |
6.在边长为1的正方体 内,作一个内切大球
内,作一个内切大球 ,再在
,再在 内的一个角顶内,作小球
内的一个角顶内,作小球 ,使它与大球外切,同时与正方体的三个面相切.则球
,使它与大球外切,同时与正方体的三个面相切.则球 的面积为.
的面积为.
 内,作一个内切大球
内,作一个内切大球 ,再在
,再在 内的一个角顶内,作小球
内的一个角顶内,作小球 ,使它与大球外切,同时与正方体的三个面相切.则球
,使它与大球外切,同时与正方体的三个面相切.则球 的面积为.
的面积为.A. | B. | C. | D. |
7.直线 与曲线
与曲线 有且仅有一个公共点,则
有且仅有一个公共点,则 的取值范围是______.
的取值范围是______.
 与曲线
与曲线 有且仅有一个公共点,则
有且仅有一个公共点,则 的取值范围是______.
的取值范围是______.8.在 的展开式中,常数项为
的展开式中,常数项为_________________ .
 的展开式中,常数项为
的展开式中,常数项为9.设 为不超过2003的正整数.如果有一个角
为不超过2003的正整数.如果有一个角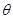 使得
使得 成立,则这种
成立,则这种  的总个数为____.
的总个数为____.
 为不超过2003的正整数.如果有一个角
为不超过2003的正整数.如果有一个角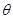 使得
使得 成立,则这种
成立,则这种  的总个数为____.
的总个数为____.10.三位数中,如果十位上的数字比百位上的数字和个位上的数字小,则称这个数为凹数,如504、764等都是凹数,那么,各个数位上无重复数字的三位数中凹数共有____________个.
11.已知 ,
, ,
, 和
和 之间有关系式
之间有关系式 ,其中
,其中 .则
.则 的最小值为
的最小值为__________________________ .
 ,
, ,
, 和
和 之间有关系式
之间有关系式 ,其中
,其中 .则
.则 的最小值为
的最小值为12.已知 、
、 、
、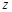 均为正整数.则方程
均为正整数.则方程 =15有_______________________组解.
=15有_______________________组解.
 、
、 、
、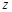 均为正整数.则方程
均为正整数.则方程 =15有_______________________组解.
=15有_______________________组解.13.设  ,函数
,函数 .
.
(1)若 ,试证:
,试证: ;
;
(2)求使函数 有最大值
有最大值 的
的 的值.
的值.
 ,函数
,函数 .
.(1)若
 ,试证:
,试证: ;
;(2)求使函数
 有最大值
有最大值 的
的 的值.
的值.14.已知  和曲线
和曲线  上的点
上的点  .是否存在
.是否存在 ,使得
,使得 称等差数列,且公差
称等差数列,且公差  ?若存在,求出
?若存在,求出 可取的所有值;若不存在,说明理由,(取
可取的所有值;若不存在,说明理由,(取 .24)
.24)
 和曲线
和曲线  上的点
上的点  .是否存在
.是否存在 ,使得
,使得 称等差数列,且公差
称等差数列,且公差  ?若存在,求出
?若存在,求出 可取的所有值;若不存在,说明理由,(取
可取的所有值;若不存在,说明理由,(取 .24)
.24)15.某市 有4个郊县(
有4个郊县( 、
、 、
、 、
、 ),如图.现有5种颜色,问有多少种不同的着色方法,使得相邻两块不同色,且每块只涂一种颜色?
),如图.现有5种颜色,问有多少种不同的着色方法,使得相邻两块不同色,且每块只涂一种颜色?
 有4个郊县(
有4个郊县( 、
、 、
、 、
、 ),如图.现有5种颜色,问有多少种不同的着色方法,使得相邻两块不同色,且每块只涂一种颜色?
),如图.现有5种颜色,问有多少种不同的着色方法,使得相邻两块不同色,且每块只涂一种颜色?
16.如图, 的外接圆圆心为
的外接圆圆心为 ,以
,以 各边为对称轴.求得
各边为对称轴.求得 的三个对称点
的三个对称点 、
、 、
、 .现将各点均擦去,仅保留
.现将各点均擦去,仅保留 、
、 、
、 ,试根据这三个点重新作出
,试根据这三个点重新作出 .
.
 的外接圆圆心为
的外接圆圆心为 ,以
,以 各边为对称轴.求得
各边为对称轴.求得 的三个对称点
的三个对称点 、
、 、
、 .现将各点均擦去,仅保留
.现将各点均擦去,仅保留 、
、 、
、 ,试根据这三个点重新作出
,试根据这三个点重新作出 .
.
 搜索
搜索
 难度系数:0.94
难度系数:0.94  答案解析
答案解析
 有奖纠错
有奖纠错
