全一卷
1.已知函数 是
是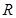 上的奇函数,
上的奇函数, 是
是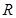 上的偶函数.若
上的偶函数.若 ,则
,则 .
.
 是
是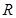 上的奇函数,
上的奇函数, 是
是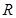 上的偶函数.若
上的偶函数.若 ,则
,则 .
.A. | B. | C. | D. |
2.有四个函数:
① ;②
;② ;③
;③ ;④
;④ .
.
其中在 上为单调增函数的是( ).
上为单调增函数的是( ).
①
 ;②
;② ;③
;③ ;④
;④ .
.其中在
 上为单调增函数的是( ).
上为单调增函数的是( ).| A.① | B.② | C.①③ | D.②④ |
3.方程 的解集为
的解集为 (其中
(其中 为无理数,
为无理数, ,
, 为实数).则
为实数).则 中所有元素的平方和等于( ).
中所有元素的平方和等于( ).
 的解集为
的解集为 (其中
(其中 为无理数,
为无理数, ,
, 为实数).则
为实数).则 中所有元素的平方和等于( ).
中所有元素的平方和等于( ).| A.0 | B.1 | C.2 | D.4 |
4.已知点 满足
满足 .则点
.则点 所在区域的面积为( ).
所在区域的面积为( ).
 满足
满足 .则点
.则点 所在区域的面积为( ).
所在区域的面积为( ).A. | B. | C. | D. |
5.将10个相同的小球装入3个编号分别为1、2、3的盒子内(每次要把10个球装完),要求每个盒子里球的个数不少于盒子的编号数,这样的装法共有( )种.
| A.9 | B.12 | C.15 | D.18 |
6.已知数列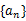 为等差数列,且
为等差数列,且 ,
, ,则
,则 等于
等于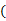
 为等差数列,且
为等差数列,且 ,
, ,则
,则 等于
等于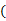
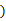
| A.80 | B.40 | C.24 | D. |
7.已知曲线 与直线
与直线 有两个交点.则
有两个交点.则 的取值范围是( ).
的取值范围是( ).
 与直线
与直线 有两个交点.则
有两个交点.则 的取值范围是( ).
的取值范围是( ).A. | B. | C. | D. |
8.过正方体 的对角线
的对角线 的截面面积为
的截面面积为 ,记
,记 和
和 分别为
分别为 的最大值和最小值.则
的最大值和最小值.则 为( ).
为( ).
 的对角线
的对角线 的截面面积为
的截面面积为 ,记
,记 和
和 分别为
分别为 的最大值和最小值.则
的最大值和最小值.则 为( ).
为( ).A. | B. | C. | D. |
9.设 ,
, ,
, .则
.则 、
、 、
、 的大小关系为( ).
的大小关系为( ).
 ,
, ,
, .则
.则 、
、 、
、 的大小关系为( ).
的大小关系为( ).A. | B. | C. | D. |
10.如果一元二次方程 中,
中, 、
、 分别是投掷骰子所得的数字,则该二次方程有两个正根的概率
分别是投掷骰子所得的数字,则该二次方程有两个正根的概率 .
.
 中,
中, 、
、 分别是投掷骰子所得的数字,则该二次方程有两个正根的概率
分别是投掷骰子所得的数字,则该二次方程有两个正根的概率 .
.A. | B. | C. | D. |
11.设 是椭圆
是椭圆 上异于长轴端点的任意一点,
上异于长轴端点的任意一点, 、
、 分别是其左、右焦点,
分别是其左、右焦点, 为中心,则
为中心,则 ______.
______.
 是椭圆
是椭圆 上异于长轴端点的任意一点,
上异于长轴端点的任意一点, 、
、 分别是其左、右焦点,
分别是其左、右焦点, 为中心,则
为中心,则 ______.
______.12.已知在 中,
中, ,
, .试用
.试用 、
、 的向量运算式表示
的向量运算式表示 ______.
______.
 中,
中, ,
, .试用
.试用 、
、 的向量运算式表示
的向量运算式表示 ______.
______.13.从3名男生和n名女生中,任选3人参加比赛,已知3人中至少有1名女生的概率为 ,则n=_____.
,则n=_____.
 ,则n=_____.
,则n=_____.14.有10名乒乓球选手进行单循环赛.比赛结果显示,没有和局,且任意5人中既有1人胜其余4人,又有1人负其余4人.则恰好胜了两场的选手有______名.
15.对于函数 ,若
,若 ,则称
,则称 为
为 的“不动点”;若
的“不动点”;若 ,则称
,则称 为
为 的“稳定点”.函数
的“稳定点”.函数 的“不动点”和“稳定点”的集合分别记为
的“不动点”和“稳定点”的集合分别记为 和
和 ,即
,即 ,
, .
.
(1)求证: ;
;
(2)若 ,且
,且 ,求实数
,求实数 的取值范围.
的取值范围.
 ,若
,若 ,则称
,则称 为
为 的“不动点”;若
的“不动点”;若 ,则称
,则称 为
为 的“稳定点”.函数
的“稳定点”.函数 的“不动点”和“稳定点”的集合分别记为
的“不动点”和“稳定点”的集合分别记为 和
和 ,即
,即 ,
, .
.(1)求证:
 ;
;(2)若
 ,且
,且 ,求实数
,求实数 的取值范围.
的取值范围.16.某制衣车间有 、
、 、
、 、
、 共4个组,各组每天生产上衣或裤子的能力如表.现在要配套生产上衣和裤子(一件上衣和一条裤子为一套).问在7天内,这4个组最多能生产多少套?
共4个组,各组每天生产上衣或裤子的能力如表.现在要配套生产上衣和裤子(一件上衣和一条裤子为一套).问在7天内,这4个组最多能生产多少套?
 、
、 、
、 、
、 共4个组,各组每天生产上衣或裤子的能力如表.现在要配套生产上衣和裤子(一件上衣和一条裤子为一套).问在7天内,这4个组最多能生产多少套?
共4个组,各组每天生产上衣或裤子的能力如表.现在要配套生产上衣和裤子(一件上衣和一条裤子为一套).问在7天内,这4个组最多能生产多少套?| |  |  |  |  |
| 上衣(件) | 8 | 9 | 7 | 6 |
| 裤子(条) | 10 | 12 | 11 | 7 |
17.设数列 满足条件:
满足条件: ,
, ,且
,且 .求证:对于任何正整数
.求证:对于任何正整数 ,都有
,都有 .
.
 满足条件:
满足条件: ,
, ,且
,且 .求证:对于任何正整数
.求证:对于任何正整数 ,都有
,都有 .
.18.在周长为定值的 中,已知
中,已知 ,且当顶点
,且当顶点 位于定点
位于定点 时,
时, 有最小值
有最小值 .
.
(1)建立适当的坐标系,求顶点 的轨迹方程;
的轨迹方程;
(2)过点 作直线与(1)中的曲线交于
作直线与(1)中的曲线交于 、
、 两点,求
两点,求 的最小值的集合.
的最小值的集合.
 中,已知
中,已知 ,且当顶点
,且当顶点 位于定点
位于定点 时,
时, 有最小值
有最小值 .
.(1)建立适当的坐标系,求顶点
 的轨迹方程;
的轨迹方程;(2)过点
 作直线与(1)中的曲线交于
作直线与(1)中的曲线交于 、
、 两点,求
两点,求 的最小值的集合.
的最小值的集合.19.已知三棱锥 的三条侧棱
的三条侧棱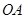 、
、 、
、 两两互相垂直,
两两互相垂直, 是底面
是底面 内的任一点,
内的任一点,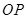 与三侧面所成的角分别为
与三侧面所成的角分别为 、
、 、
、 .求证:
.求证: .
.
 的三条侧棱
的三条侧棱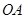 、
、 、
、 两两互相垂直,
两两互相垂直, 是底面
是底面 内的任一点,
内的任一点,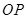 与三侧面所成的角分别为
与三侧面所成的角分别为 、
、 、
、 .求证:
.求证: .
. 搜索
搜索
 难度系数:0.65
难度系数:0.65  答案解析
答案解析
 有奖纠错
有奖纠错
