全一卷
1.将集合{1,2,……,19}中每两个互异的数作乘积,所有这种乘积的和为_________ .
2.公差为d,各项皆为正整数的等差数列 ,若a1=1919,am=1949,an=2019,则正整数m+n的最小值是____________ .
,若a1=1919,am=1949,an=2019,则正整数m+n的最小值是____________ .
 ,若a1=1919,am=1949,an=2019,则正整数m+n的最小值是____________ .
,若a1=1919,am=1949,an=2019,则正整数m+n的最小值是____________ .3.设x>0,且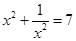 ,则
,则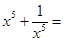 ____________ .
____________ .
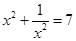 ,则
,则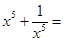 ____________ .
____________ .4.若△OAB的垂心恰是抛物线y2=4x的焦点,其中O是原点,A、B在抛物线上,则△OAB的面积S=____________ .
5.已知 是不同的正整数,若集合
是不同的正整数,若集合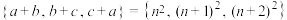 ,其中,
,其中, .则
.则 的最小值为
的最小值为_________ .
 是不同的正整数,若集合
是不同的正整数,若集合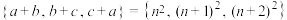 ,其中,
,其中, .则
.则 的最小值为
的最小值为6.P是正四棱锥V-ABCD的高VH的中点若点P到侧面的距离为3,到底面的距离为5,则该正四棱锥的体积为____________ .
7.△ABC的三个内角A、B、C满足:A=3B=9C,则
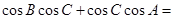 ____________ .
____________ .

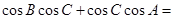 ____________ .
____________ .8.数列{an}满足: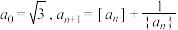 (其中[an]和{an}分别表示实数an的整数部分与小数部分),则a2019=
(其中[an]和{an}分别表示实数an的整数部分与小数部分),则a2019=____________ .
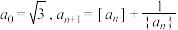 (其中[an]和{an}分别表示实数an的整数部分与小数部分),则a2019=
(其中[an]和{an}分别表示实数an的整数部分与小数部分),则a2019=9.如图所示,BE、CF分别是锐角三角形△ABC的两条高,以AB为直径的圆与直线CF相交于点M、N,以AC为直径的圆与直线BE相交于点P、Q.证明:M、N、P、Q四点共圆.

10.设椭圆C的两焦点为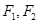 ,两准线为
,两准线为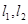 ,过椭圆上的一点P,作平行于
,过椭圆上的一点P,作平行于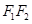 的直线,分别交
的直线,分别交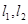 于
于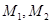 ,直线
,直线 与
与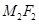 交于点Q.证明:P、F1、Q、F2四点共圆
交于点Q.证明:P、F1、Q、F2四点共圆
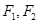 ,两准线为
,两准线为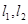 ,过椭圆上的一点P,作平行于
,过椭圆上的一点P,作平行于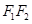 的直线,分别交
的直线,分别交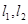 于
于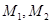 ,直线
,直线 与
与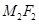 交于点Q.证明:P、F1、Q、F2四点共圆
交于点Q.证明:P、F1、Q、F2四点共圆11.将正整数数列1,2,3,…中凡是被4整除以及被4除余1的项全部删去,剩下的数按自小到大的顺序排成数列 ,再将数列
,再将数列 中,凡是下标被4整除以及被4除余1的项全部删去,剩下的项按自小到大的顺序排成数列
中,凡是下标被4整除以及被4除余1的项全部删去,剩下的项按自小到大的顺序排成数列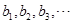 .证明:每个大于1的奇平方数,都是数列{bn}中的两个相邻项的和.
.证明:每个大于1的奇平方数,都是数列{bn}中的两个相邻项的和.
 ,再将数列
,再将数列 中,凡是下标被4整除以及被4除余1的项全部删去,剩下的项按自小到大的顺序排成数列
中,凡是下标被4整除以及被4除余1的项全部删去,剩下的项按自小到大的顺序排成数列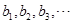 .证明:每个大于1的奇平方数,都是数列{bn}中的两个相邻项的和.
.证明:每个大于1的奇平方数,都是数列{bn}中的两个相邻项的和.12.试求所有由互异正奇数构成的三元集{a,b,c},使其满足: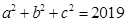 .
.
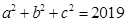 .
. 搜索
搜索
 难度系数:0.65
难度系数:0.65  答案解析
答案解析
 有奖纠错
有奖纠错
