全一卷
1.记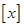 表示不大于x的最大整数.设集合
表示不大于x的最大整数.设集合 ,
, ,则
,则 =.
=.
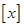 表示不大于x的最大整数.设集合
表示不大于x的最大整数.设集合 ,
, ,则
,则 =.
=.A. | B. |
C. | D. |
2.若 ,则
,则 .
.
 ,则
,则 .
.| A.-1 | B.1 | C.2005 | D.2007 |
3.四边形的各顶点位于一个边长为1的正方形各边上.若四条边长的平方和为t,则t的取值区间是.
A. | B. | C. | D. |
4.如图,在正方体 中,P为棱AB上一点,过点P在空间作直线l,使l与平面ABCD和
中,P为棱AB上一点,过点P在空间作直线l,使l与平面ABCD和 均成30°角.则这样的直线条数是( ).
均成30°角.则这样的直线条数是( ).

 中,P为棱AB上一点,过点P在空间作直线l,使l与平面ABCD和
中,P为棱AB上一点,过点P在空间作直线l,使l与平面ABCD和 均成30°角.则这样的直线条数是( ).
均成30°角.则这样的直线条数是( ).
| A.1 | B.2 | C.3 | D.4 |
5.等腰 中,斜边
中,斜边 ,一椭圆以C为其焦点,另一个焦点在线段AB上,且椭圆经过点A、B.则该椭圆的标准方程是(焦点在x轴上).
,一椭圆以C为其焦点,另一个焦点在线段AB上,且椭圆经过点A、B.则该椭圆的标准方程是(焦点在x轴上).
 中,斜边
中,斜边 ,一椭圆以C为其焦点,另一个焦点在线段AB上,且椭圆经过点A、B.则该椭圆的标准方程是(焦点在x轴上).
,一椭圆以C为其焦点,另一个焦点在线段AB上,且椭圆经过点A、B.则该椭圆的标准方程是(焦点在x轴上).A. |
B. |
C. |
D. |
6.将正方形的每条边8等分,再取分点为顶点(不包括正方形的顶点),可以得到不同的三角形个.
| A.1372 | B.2024 | C.3136 | D.4495 |
7.等差数列 的前m项和为90,前2m项和为360.则前4m项和为_______.
的前m项和为90,前2m项和为360.则前4m项和为_______.
 的前m项和为90,前2m项和为360.则前4m项和为_______.
的前m项和为90,前2m项和为360.则前4m项和为_______.8.已知 ,且
,且 ,则cos(x+2y)的值为
,则cos(x+2y)的值为____ .
 ,且
,且 ,则cos(x+2y)的值为
,则cos(x+2y)的值为9.100只椅子排成一个圆圈,有 个人坐在椅子上,使得再有一个人入座时,他总与原来
个人坐在椅子上,使得再有一个人入座时,他总与原来 个人中某一个坐在相邻椅子上,则
个人中某一个坐在相邻椅子上,则 的最小值是______.
的最小值是______.
 个人坐在椅子上,使得再有一个人入座时,他总与原来
个人坐在椅子上,使得再有一个人入座时,他总与原来 个人中某一个坐在相邻椅子上,则
个人中某一个坐在相邻椅子上,则 的最小值是______.
的最小值是______.10.在△ABC 中,已知 AB = 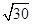 ,AC =
,AC =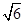 ,BC =
,BC = ,有一点 D 使得 AD 平分 BC ,且∠ADB =90°,比值
,有一点 D 使得 AD 平分 BC ,且∠ADB =90°,比值 能写成
能写成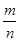 的形式,这里 m 、n 是互质的正整数.则 m +n =_______.
的形式,这里 m 、n 是互质的正整数.则 m +n =_______.
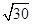 ,AC =
,AC =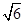 ,BC =
,BC = ,有一点 D 使得 AD 平分 BC ,且∠ADB =90°,比值
,有一点 D 使得 AD 平分 BC ,且∠ADB =90°,比值 能写成
能写成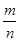 的形式,这里 m 、n 是互质的正整数.则 m +n =_______.
的形式,这里 m 、n 是互质的正整数.则 m +n =_______.11.设 是棱长为1的正方体.则上底面ABCD的内切圆上的点P与过顶点A、B、
是棱长为1的正方体.则上底面ABCD的内切圆上的点P与过顶点A、B、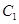 、
、 的圆上的点Q之间的最小距离是________.
的圆上的点Q之间的最小距离是________.
 是棱长为1的正方体.则上底面ABCD的内切圆上的点P与过顶点A、B、
是棱长为1的正方体.则上底面ABCD的内切圆上的点P与过顶点A、B、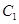 、
、 的圆上的点Q之间的最小距离是________.
的圆上的点Q之间的最小距离是________.12.—项“过关游戏”的规则规定:在第n关要抛一枚骰子n次,如果这n次抛掷所出现的点数之和大于 ,则算过关.那么,连过前3关的概率为_______.
,则算过关.那么,连过前3关的概率为_______.
 ,则算过关.那么,连过前3关的概率为_______.
,则算过关.那么,连过前3关的概率为_______.13.是否存在最小的正整数t,使得不等式 ①对任何正整数n恒成立?证明你的结论.
①对任何正整数n恒成立?证明你的结论.
 ①对任何正整数n恒成立?证明你的结论.
①对任何正整数n恒成立?证明你的结论.14.设x、y、z为正实数.求函数 的最小值.
的最小值.
 的最小值.
的最小值.15.设A、B分别为椭圆 和双曲线
和双曲线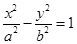 的公共左、右顶点,P、Q分别为双曲线和椭圆上不同于A、B的动点,且满足
的公共左、右顶点,P、Q分别为双曲线和椭圆上不同于A、B的动点,且满足 .设直线AP、BP、AQ、BQ的斜率分别为
.设直线AP、BP、AQ、BQ的斜率分别为 、
、 、
、 、
、 .
.
(1)求证: ;
;
(2)设 、
、 分别为椭圆和双曲线的右焦点,若
分别为椭圆和双曲线的右焦点,若 ,求
,求 的值.
的值.
 和双曲线
和双曲线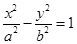 的公共左、右顶点,P、Q分别为双曲线和椭圆上不同于A、B的动点,且满足
的公共左、右顶点,P、Q分别为双曲线和椭圆上不同于A、B的动点,且满足 .设直线AP、BP、AQ、BQ的斜率分别为
.设直线AP、BP、AQ、BQ的斜率分别为 、
、 、
、 、
、 .
.(1)求证:
 ;
;(2)设
 、
、 分别为椭圆和双曲线的右焦点,若
分别为椭圆和双曲线的右焦点,若 ,求
,求 的值.
的值.16.将m位性别相同的客人,按如下方法安排入住 这n个房间:首先,安排1位客人和余下的客人的
这n个房间:首先,安排1位客人和余下的客人的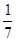 入住房间
入住房间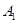 ;然后,从余下的客人中安排2位客人和再次余下的客人的
;然后,从余下的客人中安排2位客人和再次余下的客人的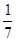 入住房间
入住房间 ;依此类推,第几号房就安排几位客人和余下的客人的
;依此类推,第几号房就安排几位客人和余下的客人的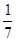 入住.这样,最后一间房间
入住.这样,最后一间房间 正好安排最后余下的n位客人.试求客人的数和客房的房间数,以及每间客房入住客人的数.
正好安排最后余下的n位客人.试求客人的数和客房的房间数,以及每间客房入住客人的数.
 这n个房间:首先,安排1位客人和余下的客人的
这n个房间:首先,安排1位客人和余下的客人的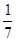 入住房间
入住房间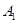 ;然后,从余下的客人中安排2位客人和再次余下的客人的
;然后,从余下的客人中安排2位客人和再次余下的客人的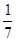 入住房间
入住房间 ;依此类推,第几号房就安排几位客人和余下的客人的
;依此类推,第几号房就安排几位客人和余下的客人的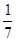 入住.这样,最后一间房间
入住.这样,最后一间房间 正好安排最后余下的n位客人.试求客人的数和客房的房间数,以及每间客房入住客人的数.
正好安排最后余下的n位客人.试求客人的数和客房的房间数,以及每间客房入住客人的数. 搜索
搜索
 难度系数:0.65
难度系数:0.65  答案解析
答案解析
 有奖纠错
有奖纠错
