全一卷
1.已知全集 ,集合
,集合 ,
, ,则
,则
 ,集合
,集合 ,
, ,则
,则
A. | B. |
C. | D. |
2.渐近线方程为 的双曲线的离心率是
的双曲线的离心率是
 的双曲线的离心率是
的双曲线的离心率是A. | B.1 |
C. | D.2 |
3.若实数 满足约束条件
满足约束条件 ,则
,则 的最大值是
的最大值是
 满足约束条件
满足约束条件 ,则
,则 的最大值是
的最大值是A. | B.1 |
| C.10 | D.12 |
4.祖暅是我国南北朝时代的伟大科学家,他提出的“幂势既同,则积不容异”称为祖暅原理,利用该原理可以得到柱体的体积公式 ,其中
,其中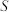 是柱体的底面积,
是柱体的底面积,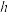 是柱体的高.若某柱体的三视图如图所示(单位:cm),则该柱体的体积(单位:cm3)是
是柱体的高.若某柱体的三视图如图所示(单位:cm),则该柱体的体积(单位:cm3)是

 ,其中
,其中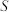 是柱体的底面积,
是柱体的底面积,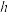 是柱体的高.若某柱体的三视图如图所示(单位:cm),则该柱体的体积(单位:cm3)是
是柱体的高.若某柱体的三视图如图所示(单位:cm),则该柱体的体积(单位:cm3)是
| A.158 | B.162 |
| C.182 | D.324 |
5.若 ,则“
,则“ ”是 “
”是 “ ”的
”的
 ,则“
,则“ ”是 “
”是 “ ”的
”的| A.充分不必要条件 | B.必要不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
6.在同一直角坐标系中,函数 且
且 的图象可能是
的图象可能是
 且
且 的图象可能是
的图象可能是A. | B. |
C. | D.  |
7.设0<a<1,则随机变量X的分布列是
则当a在(0,1)内增大时( )
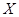 |  |  | 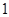 |
 |  |  |  |
则当a在(0,1)内增大时( )
A. 增大 增大 | B. 减小 减小 |
C. 先增大后减小 先增大后减小 | D. 先减小后增大 先减小后增大 |
8.设三棱锥 的底面是正三角形,侧棱长均相等,
的底面是正三角形,侧棱长均相等, 是棱
是棱 上的点(不含端点),记直线
上的点(不含端点),记直线 与直线
与直线 所成角为
所成角为 ,直线
,直线 与平面
与平面 所成角为
所成角为 ,二面角
,二面角 的平面角为
的平面角为 ,则
,则
 的底面是正三角形,侧棱长均相等,
的底面是正三角形,侧棱长均相等, 是棱
是棱 上的点(不含端点),记直线
上的点(不含端点),记直线 与直线
与直线 所成角为
所成角为 ,直线
,直线 与平面
与平面 所成角为
所成角为 ,二面角
,二面角 的平面角为
的平面角为 ,则
,则A. | B. |
C. | D. |
9.已知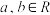 ,函数
,函数 ,若函数
,若函数 恰有三个零点,则
恰有三个零点,则
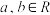 ,函数
,函数 ,若函数
,若函数 恰有三个零点,则
恰有三个零点,则A. | B. |
C. | D. |
10.设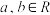 ,数列
,数列 中,
中, ,
,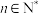 ,则
,则
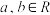 ,数列
,数列 中,
中, ,
,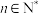 ,则
,则A.当 | B.当 |
C.当 | D.当 |
11.复数 (
(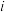 为虚数单位),则
为虚数单位),则
________ .
 (
(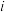 为虚数单位),则
为虚数单位),则
12.已知圆 的圆心坐标是
的圆心坐标是 ,半径长是
,半径长是 .若直线
.若直线 与圆相切于点
与圆相切于点 ,则
,则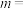
_____ ,
______ .
 的圆心坐标是
的圆心坐标是 ,半径长是
,半径长是 .若直线
.若直线 与圆相切于点
与圆相切于点 ,则
,则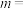

13.在二项式 的展开式中,常数项是
的展开式中,常数项是________ ;系数为有理数的项的个数是_______ .
 的展开式中,常数项是
的展开式中,常数项是14.在 中,
中, ,
, ,
, ,点
,点 在线段
在线段 上,若
上,若 ,则
,则
____ ;
________ .
 中,
中, ,
, ,
, ,点
,点 在线段
在线段 上,若
上,若 ,则
,则

15.已知椭圆 的左焦点为
的左焦点为 ,点
,点 在椭圆上且在
在椭圆上且在 轴的上方,若线段
轴的上方,若线段 的中点在以原点
的中点在以原点 为圆心,
为圆心, 为半径的圆上,则直线
为半径的圆上,则直线 的斜率是
的斜率是_______ .
 的左焦点为
的左焦点为 ,点
,点 在椭圆上且在
在椭圆上且在 轴的上方,若线段
轴的上方,若线段 的中点在以原点
的中点在以原点 为圆心,
为圆心, 为半径的圆上,则直线
为半径的圆上,则直线 的斜率是
的斜率是16.已知 ,函数
,函数 ,若存在
,若存在 ,使得
,使得 ,则实数
,则实数 的最大值是
的最大值是____ .
 ,函数
,函数 ,若存在
,若存在 ,使得
,使得 ,则实数
,则实数 的最大值是
的最大值是17.已知正方形 的边长为1,当每个
的边长为1,当每个 取遍
取遍 时,
时, 的最小值是
的最小值是________ ;最大值是_______ .
 的边长为1,当每个
的边长为1,当每个 取遍
取遍 时,
时, 的最小值是
的最小值是18.设函数 .
.
(1)已知 函数
函数 是偶函数,求
是偶函数,求 的值;
的值;
(2)求函数 的值域.
的值域.
 .
.(1)已知
 函数
函数 是偶函数,求
是偶函数,求 的值;
的值;(2)求函数
 的值域.
的值域.19.如图,已知三棱柱 ,平面
,平面 平面
平面 ,
, ,
, 分别是
分别是 的中点.
的中点.

(1)证明: ;
;
(2)求直线 与平面
与平面 所成角的余弦值.
所成角的余弦值.
 ,平面
,平面 平面
平面 ,
, ,
, 分别是
分别是 的中点.
的中点.
(1)证明:
 ;
;(2)求直线
 与平面
与平面 所成角的余弦值.
所成角的余弦值.20.设等差数列 的前
的前 项和为
项和为 ,
, ,
, ,数列
,数列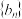 满足:对每
满足:对每 成等比数列.
成等比数列.
(1)求数列 的通项公式;
的通项公式;
(2)记 证明:
证明:
 的前
的前 项和为
项和为 ,
, ,
, ,数列
,数列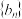 满足:对每
满足:对每 成等比数列.
成等比数列.(1)求数列
 的通项公式;
的通项公式;(2)记
 证明:
证明:
21.如图,已知点 为抛物线
为抛物线 的焦点,过点
的焦点,过点 的直线交抛物线于
的直线交抛物线于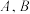 两点,点
两点,点 在抛物线上,使得
在抛物线上,使得 的重心
的重心 在
在 轴上,直线
轴上,直线 交
交 轴于点
轴于点 ,且
,且 在点
在点 右侧.记
右侧.记 的面积为
的面积为 .
.

(1)求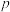 的值及抛物线的准线方程;
的值及抛物线的准线方程;
(2)求 的最小值及此时点
的最小值及此时点 的坐标.
的坐标.
 为抛物线
为抛物线 的焦点,过点
的焦点,过点 的直线交抛物线于
的直线交抛物线于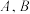 两点,点
两点,点 在抛物线上,使得
在抛物线上,使得 的重心
的重心 在
在 轴上,直线
轴上,直线 交
交 轴于点
轴于点 ,且
,且 在点
在点 右侧.记
右侧.记 的面积为
的面积为 .
.
(1)求
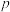 的值及抛物线的准线方程;
的值及抛物线的准线方程;(2)求
 的最小值及此时点
的最小值及此时点 的坐标.
的坐标.22.已知实数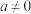 ,设函数
,设函数
(1)当 时,求函数
时,求函数 的单调区间;
的单调区间;
(2)对任意 均有
均有 求
求 的取值范围.
的取值范围.
注: 为自然对数的底数.
为自然对数的底数.
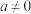 ,设函数
,设函数
(1)当
 时,求函数
时,求函数 的单调区间;
的单调区间;(2)对任意
 均有
均有 求
求 的取值范围.
的取值范围.注:
 为自然对数的底数.
为自然对数的底数. 搜索
搜索
 难度系数:0.85
难度系数:0.85  答案解析
答案解析
 有奖纠错
有奖纠错
