全一卷
1.已知实数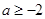 ,且
,且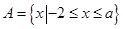 ,
,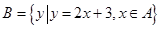 ,
,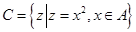 .若
.若 ,则
,则 的取值范围是______________。
的取值范围是______________。
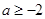 ,且
,且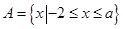 ,
,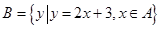 ,
,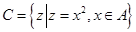 .若
.若 ,则
,则 的取值范围是______________。
的取值范围是______________。2.△ABC的三边分别为a、b、c,点O为△ABC的外心,已知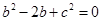 ,那么
,那么 的取值范围是____________ .
的取值范围是____________ .
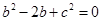 ,那么
,那么 的取值范围是____________ .
的取值范围是____________ .3.已知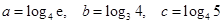 ,则a、b、c的大小关系是____________ .
,则a、b、c的大小关系是____________ .
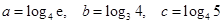 ,则a、b、c的大小关系是____________ .
,则a、b、c的大小关系是____________ .4.若方程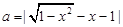 有实数解,则实数a的取值范围是____________ .
有实数解,则实数a的取值范围是____________ .
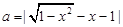 有实数解,则实数a的取值范围是____________ .
有实数解,则实数a的取值范围是____________ .5.在数列{an}中,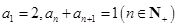 ,设Sn为数列{an}的前n项和,则
,设Sn为数列{an}的前n项和,则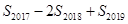 的值为____________ .
的值为____________ .
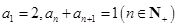 ,设Sn为数列{an}的前n项和,则
,设Sn为数列{an}的前n项和,则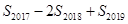 的值为____________ .
的值为____________ .6.在复平面内,复数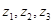 对应的点分别为
对应的点分别为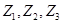 .若
.若 ,
,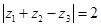 ,则
,则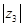 的取值范围是
的取值范围是______ .
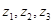 对应的点分别为
对应的点分别为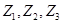 .若
.若 ,
,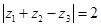 ,则
,则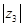 的取值范围是
的取值范围是7.已知函数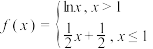 ,若
,若 ,且
,且 ,则
,则 的最小值是
的最小值是_____ .
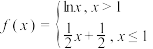 ,若
,若 ,且
,且 ,则
,则 的最小值是
的最小值是8.已知椭圆 的左、右焦点分别为
的左、右焦点分别为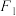 、
、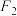 ,过椭圆的右焦点
,过椭圆的右焦点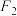 作一条直线
作一条直线 交椭圆于点
交椭圆于点 、
、 .则
.则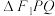 内切圆面积的最大值是
内切圆面积的最大值是_________ .
 的左、右焦点分别为
的左、右焦点分别为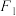 、
、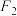 ,过椭圆的右焦点
,过椭圆的右焦点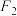 作一条直线
作一条直线 交椭圆于点
交椭圆于点 、
、 .则
.则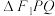 内切圆面积的最大值是
内切圆面积的最大值是9.已知x>0,y>0,且 ,则x+2y的最小值为____________ .
,则x+2y的最小值为____________ .
 ,则x+2y的最小值为____________ .
,则x+2y的最小值为____________ .10.在平面直角坐标系中定义点 之间的交通距离为
之间的交通距离为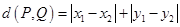 .
.
若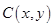 到点
到点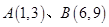 的交通距离相等,其中,实数
的交通距离相等,其中,实数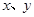 满足
满足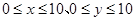 ,则所有满足条件的点
,则所有满足条件的点 的轨迹的长之和为____________.
的轨迹的长之和为____________.
 之间的交通距离为
之间的交通距离为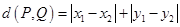 .
.若
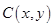 到点
到点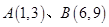 的交通距离相等,其中,实数
的交通距离相等,其中,实数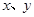 满足
满足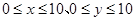 ,则所有满足条件的点
,则所有满足条件的点 的轨迹的长之和为____________.
的轨迹的长之和为____________.11.已知向量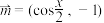 ,
,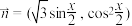 ,设函数
,设函数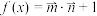 .
.
(1)若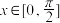 ,
,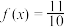 ,求
,求 的值;
的值;
(2)在△ 中,角
中,角 ,
, ,
, 的对边分别是
的对边分别是 且满足
且满足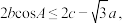 求
求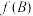 的取值范围.
的取值范围.
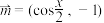 ,
,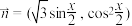 ,设函数
,设函数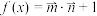 .
.(1)若
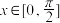 ,
,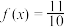 ,求
,求 的值;
的值;(2)在△
 中,角
中,角 ,
, ,
, 的对边分别是
的对边分别是 且满足
且满足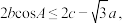 求
求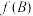 的取值范围.
的取值范围.12.2018年全国数学奥赛试行改革:在高二一年中举行5次全区竞赛,学生如果其中2次成绩达全区前20名即可进入省队培训,不用参加其余的竞赛,而每个学生最多也只能参加5次竞赛.规定:若前4次竞赛成绩都没有达全区前20名,则第5次不能参加竞赛.假设某学生每次成绩达全区前20名的概率都是 ,每次竞赛成绩达全区前20名与否互相独立.
,每次竞赛成绩达全区前20名与否互相独立.
(1)求该学生进入省队的概率.
(2)如果该学生进入省队或参加完5次竞赛就结束,记该学生参加竞赛的次数为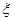 ,求
,求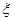 的分布列及
的分布列及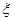 的数学期望.
的数学期望.
 ,每次竞赛成绩达全区前20名与否互相独立.
,每次竞赛成绩达全区前20名与否互相独立.(1)求该学生进入省队的概率.
(2)如果该学生进入省队或参加完5次竞赛就结束,记该学生参加竞赛的次数为
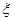 ,求
,求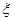 的分布列及
的分布列及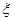 的数学期望.
的数学期望.13.已知数列 中,
中,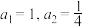 ,且
,且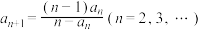
(1)求数列 的通项公式;
的通项公式;
(2)证明:对一切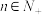 ,有
,有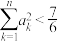
 中,
中,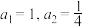 ,且
,且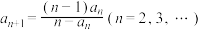
(1)求数列
 的通项公式;
的通项公式;(2)证明:对一切
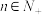 ,有
,有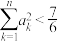
14.已知三棱锥P-ABC的平面展开图中,四边形ABCD为边长等于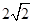 的正方形,△ABE和△BCF均为正三角形,在三棱锥P-ABC中:
的正方形,△ABE和△BCF均为正三角形,在三棱锥P-ABC中:

(1)证明:平面PAC⊥平面ABC;
(2)若点M为棱PA上一点且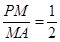 ,求二面角P-BC-M的余弦值.
,求二面角P-BC-M的余弦值.
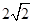 的正方形,△ABE和△BCF均为正三角形,在三棱锥P-ABC中:
的正方形,△ABE和△BCF均为正三角形,在三棱锥P-ABC中:
(1)证明:平面PAC⊥平面ABC;
(2)若点M为棱PA上一点且
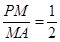 ,求二面角P-BC-M的余弦值.
,求二面角P-BC-M的余弦值.15.易知椭圆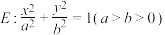 ,其短轴为4,离心率为e1.双曲线
,其短轴为4,离心率为e1.双曲线 的渐近线为
的渐近线为 ,离心率为e2,且
,离心率为e2,且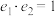 .
.
(1)求椭圆E的方程;
(2)设椭圆E的右焦点为F,过点G(4,0)斜率不为0的直线交椭圆E于M、N两点设直线FM和FN的斜率为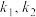 ,试判断
,试判断 是否为定值,若是定值,求出该定值;若不是定值,请说明理由.
是否为定值,若是定值,求出该定值;若不是定值,请说明理由.
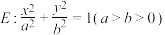 ,其短轴为4,离心率为e1.双曲线
,其短轴为4,离心率为e1.双曲线 的渐近线为
的渐近线为 ,离心率为e2,且
,离心率为e2,且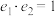 .
.(1)求椭圆E的方程;
(2)设椭圆E的右焦点为F,过点G(4,0)斜率不为0的直线交椭圆E于M、N两点设直线FM和FN的斜率为
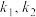 ,试判断
,试判断 是否为定值,若是定值,求出该定值;若不是定值,请说明理由.
是否为定值,若是定值,求出该定值;若不是定值,请说明理由.16.已知函数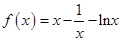 .
.
(1)若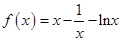 在
在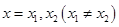 处导数相等,证明:
处导数相等,证明: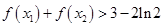 ;
;
(2)若对于任意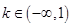 ,直线
,直线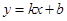 与曲线
与曲线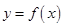 都有唯一公共点,求实数
都有唯一公共点,求实数 的取值范围.
的取值范围.
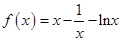 .
.(1)若
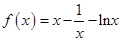 在
在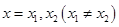 处导数相等,证明:
处导数相等,证明: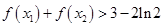 ;
;(2)若对于任意
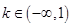 ,直线
,直线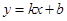 与曲线
与曲线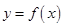 都有唯一公共点,求实数
都有唯一公共点,求实数 的取值范围.
的取值范围. 搜索
搜索
 难度系数:0.65
难度系数:0.65  答案解析
答案解析
 有奖纠错
有奖纠错
