全一卷
1.若 ,则
,则 ( ).
( ).
 ,则
,则 ( ).
( ).| A.既是奇函数又是增函数. |
| B.既是奇函数又是减函数. |
| C.既是偶函数又是增函数. |
| D.既是偶函数又是减函数. |
2.如图,设P、M、N分别是正方体的棱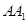 ,AD,AB上非顶点的任意点.
,AD,AB上非顶点的任意点.

① 的外心必在
的外心必在 的某一边上;
的某一边上;
② 的外心必在
的外心必在 的内部;
的内部;
③ 的垂心必是点A在平面PMN上的射影;
的垂心必是点A在平面PMN上的射影;
④若线段AP、AM、AN的长分别为a、b、c,则 .其中( ).
.其中( ).
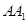 ,AD,AB上非顶点的任意点.
,AD,AB上非顶点的任意点.
①
 的外心必在
的外心必在 的某一边上;
的某一边上;②
 的外心必在
的外心必在 的内部;
的内部;③
 的垂心必是点A在平面PMN上的射影;
的垂心必是点A在平面PMN上的射影;④若线段AP、AM、AN的长分别为a、b、c,则
 .其中( ).
.其中( ).| A.只有①、④正确. |
| B.只有③、④正确. |
| C.只有②、③、④正确. |
| D.只有②、③正确. |
3.方程 与
与 的曲线在同一坐标系中的示意图应是( ).
的曲线在同一坐标系中的示意图应是( ).
 与
与 的曲线在同一坐标系中的示意图应是( ).
的曲线在同一坐标系中的示意图应是( ).A. | B. |
C. | D. |
4.设 是整数等差列,n为偶数.甲:它的各项之和
是整数等差列,n为偶数.甲:它的各项之和 是偶数.乙:它的公差d是偶数.那么甲是乙的( ).
是偶数.乙:它的公差d是偶数.那么甲是乙的( ).
 是整数等差列,n为偶数.甲:它的各项之和
是整数等差列,n为偶数.甲:它的各项之和 是偶数.乙:它的公差d是偶数.那么甲是乙的( ).
是偶数.乙:它的公差d是偶数.那么甲是乙的( ).| A.充分条件,也是必要条件. |
| B.充分条件,但非必要条件. |
| C.必要条件,但非充分条件. |
| D.既非充分条件,也非必要条件. |
5.下列四个命题
①若三个平面两两相交,则它们的交线只能平行或重合;
②若a、b是异面直线,则过不在a、b上的任一点一定可以作一条直线和a、b都相交;
③正三棱锥 的底面边长为a,侧棱长为b,若过SA、SB的中点作平行于侧棱SC的截面,则截面面积为
的底面边长为a,侧棱长为b,若过SA、SB的中点作平行于侧棱SC的截面,则截面面积为 ;
;
④过球面上任意给定两点的平面与球面相截时其截面面积最大,则这样的平面只有一个.
其中( ).
①若三个平面两两相交,则它们的交线只能平行或重合;
②若a、b是异面直线,则过不在a、b上的任一点一定可以作一条直线和a、b都相交;
③正三棱锥
 的底面边长为a,侧棱长为b,若过SA、SB的中点作平行于侧棱SC的截面,则截面面积为
的底面边长为a,侧棱长为b,若过SA、SB的中点作平行于侧棱SC的截面,则截面面积为 ;
;④过球面上任意给定两点的平面与球面相截时其截面面积最大,则这样的平面只有一个.
其中( ).
| A.只有①,②成立. |
| B.只有③成立. |
| C.只有④ 成立. |
| D.①、②、③、④都不成立. |
6. 的值等于________.
的值等于________.
 的值等于________.
的值等于________.7.设m、n、p都是正实数,且 ,则
,则 的最小值为________.
的最小值为________.
 ,则
,则 的最小值为________.
的最小值为________.8.设 则
则 的值为________.
的值为________.
 则
则 的值为________.
的值为________.9.若 ,则二元方程
,则二元方程 的解为________.
的解为________.
 ,则二元方程
,则二元方程 的解为________.
的解为________.10.在-1,0,1,2,3,4,5, 6,7,8,9中,若适当选择两个不同的数分别作为对数的底数和真数,则所有可能得到的不相等的对数值共________个.
11.如图,设正方形ABCD的边长为a,以点C为圆心、a为半径的圆与以AB为直径的圆相交于P.试用解析法求 的面积.
的面积.
 的面积.
的面积.
12.已知:实数 满足
满足 ,且
,且 .求证
.求证 .提示:先证
.提示:先证 ,再证
,再证 .
.
 满足
满足 ,且
,且 .求证
.求证 .提示:先证
.提示:先证 ,再证
,再证 .
.13.设 的三边a、b、c的长均为整数,且其内切圆半径为1.
的三边a、b、c的长均为整数,且其内切圆半径为1.
试证: 是直角三角形.
是直角三角形.
 的三边a、b、c的长均为整数,且其内切圆半径为1.
的三边a、b、c的长均为整数,且其内切圆半径为1.试证:
 是直角三角形.
是直角三角形.14.已知 为正整数数列,
为正整数数列, .求
.求 .
.
 为正整数数列,
为正整数数列, .求
.求 .
.15.给定一个由 个小正方形拼成的棋盘形方格,这些小正方形的颜色黑白相间(如图).
个小正方形拼成的棋盘形方格,这些小正方形的颜色黑白相间(如图).

现定义一种运算A:把位于第i行的所有小正方形和位于第j列的所有小正方形都换成相反的颜色,即黑色的小正方形换成白色的,白色的小正方形换成黑色的,这里 .我们把A称为在位于第i行第j列上的小正方形上的一次运算.试问:能否经过若干次上述运算把棋盘上的所有小正方形全部换成同一种颜色?证明你的结论.
.我们把A称为在位于第i行第j列上的小正方形上的一次运算.试问:能否经过若干次上述运算把棋盘上的所有小正方形全部换成同一种颜色?证明你的结论.
 个小正方形拼成的棋盘形方格,这些小正方形的颜色黑白相间(如图).
个小正方形拼成的棋盘形方格,这些小正方形的颜色黑白相间(如图).
现定义一种运算A:把位于第i行的所有小正方形和位于第j列的所有小正方形都换成相反的颜色,即黑色的小正方形换成白色的,白色的小正方形换成黑色的,这里
 .我们把A称为在位于第i行第j列上的小正方形上的一次运算.试问:能否经过若干次上述运算把棋盘上的所有小正方形全部换成同一种颜色?证明你的结论.
.我们把A称为在位于第i行第j列上的小正方形上的一次运算.试问:能否经过若干次上述运算把棋盘上的所有小正方形全部换成同一种颜色?证明你的结论. 搜索
搜索
 难度系数:0.94
难度系数:0.94  答案解析
答案解析
 有奖纠错
有奖纠错
