全一卷
1.已知等差数列{an}的公差d≠0,且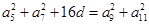 ,则{an}的前15项之和S15等于( )
,则{an}的前15项之和S15等于( )
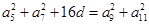 ,则{an}的前15项之和S15等于( )
,则{an}的前15项之和S15等于( )| A.15 | B.16 | C.30 | D.32 |
2.方程组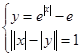 的解的组数是( )
的解的组数是( )
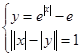 的解的组数是( )
的解的组数是( )| A.5 | B.6 | C.7 | D.8 |
3.在Rt△ABC中,∠B=90°,AB=15,BC=20.则顶点B与斜边各点的连线中(含边AB、BC)长度为整数的线段条数是( )
| A.9 | B.10 | C.11 | D.12 |
4.已知正三棱锥侧面与底面所成二面角的余弦值为 ,则此三棱锥的高h与其内切球半径r之比是( )
,则此三棱锥的高h与其内切球半径r之比是( )
 ,则此三棱锥的高h与其内切球半径r之比是( )
,则此三棱锥的高h与其内切球半径r之比是( )| A.5 | B.6 | C.7 | D.8 |
5.设椭圆C: 的左、右焦点分别为
的左、右焦点分别为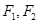 ,其焦距为2c.点
,其焦距为2c.点 在椭圆的内部,点M是椭圆C上的动点,且
在椭圆的内部,点M是椭圆C上的动点,且 恒成立,则椭圆C的离心率的取值范围是( )
恒成立,则椭圆C的离心率的取值范围是( )
 的左、右焦点分别为
的左、右焦点分别为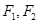 ,其焦距为2c.点
,其焦距为2c.点 在椭圆的内部,点M是椭圆C上的动点,且
在椭圆的内部,点M是椭圆C上的动点,且 恒成立,则椭圆C的离心率的取值范围是( )
恒成立,则椭圆C的离心率的取值范围是( )A. | B. | C. | D. |
6.如图,在△ABC中,AB=30,AC=20,S△ABC=210,D、E分别为边AB、AC的中点,∠BAC的平分线分别与DE、BC交于点F、G,则四边形BGFD的面积为________.

7.已知函数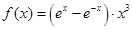 ,若m满足
,若m满足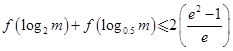 ,则实数m的取值范围是____________ .
,则实数m的取值范围是____________ .
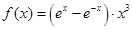 ,若m满足
,若m满足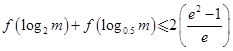 ,则实数m的取值范围是____________ .
,则实数m的取值范围是____________ .8.若半径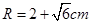 的空心球内部装有四个半径为r的实心球,则r所能取得的最大值为____________
的空心球内部装有四个半径为r的实心球,则r所能取得的最大值为____________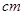 .
.
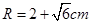 的空心球内部装有四个半径为r的实心球,则r所能取得的最大值为____________
的空心球内部装有四个半径为r的实心球,则r所能取得的最大值为____________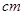 .
.9.在△ABC中, .则
.则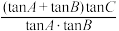

____________ .
 .则
.则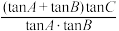

10.已知正项数列 的前n项和为
的前n项和为 .若
.若 ,
,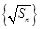 均为公差为d的等差数列,则
均为公差为d的等差数列,则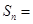 ________.
________.
 的前n项和为
的前n项和为 .若
.若 ,
,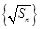 均为公差为d的等差数列,则
均为公差为d的等差数列,则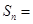 ________.
________.11.已知m∈{11,13,15,17,19},n∈{2000,2001,…,2019},则mn的个位数是1的概率为____________ .
12.已知方程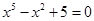 的五个根分别为
的五个根分别为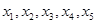 ,f(x)=x2+1,则
,f(x)=x2+1,则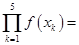 ____________ .
____________ .
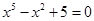 的五个根分别为
的五个根分别为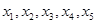 ,f(x)=x2+1,则
,f(x)=x2+1,则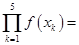 ____________ .
____________ .13.若(a+b)n的展开式中有连续三项的二项式系数成等差数列,则最大的三位正整数n=____________ .
14.求平面区域 的面积为____________ .
的面积为____________ .
 的面积为____________ .
的面积为____________ .15.已知集合A={1,2,3,…,2019},对于集合A的每一个非空子集的所有元素,计算它们乘积的倒数.则所有这些倒数的和为____________ .
16.我们知道,目前最常见的骰子是六面骰,它是一颗正立方体,上面分别有一到六个洞(或数字),其相对两面之数字和必为七.显然,掷一次六面骰,只能产生六个数之一(正上面).现欲要求你设计一个“十进制骰”,使其掷一次能产生0~9这十个数之一,而且每个数字产生的可能性一样.请问:你能设计出这样的骰子吗?若能,请写出你的设计方案;若不能,写出理由.
17.已知定长为4的线段AB的两端点,分别在两条相交直线x±2y=0上移动.
(1)设线段AB的中点为G,求点G的轨迹C的方程;
(2)若由点P向曲线C作出的两条切线互相垂直,求证:动点P在定圆上.
(1)设线段AB的中点为G,求点G的轨迹C的方程;
(2)若由点P向曲线C作出的两条切线互相垂直,求证:动点P在定圆上.
18.已知正项数列{an}的前n项和为Sn,且 .
.
(1)求数列{an}的通项公式;
(2)求证: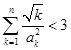 .
.
 .
.(1)求数列{an}的通项公式;
(2)求证:
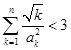 .
. 搜索
搜索
 难度系数:0.65
难度系数:0.65  答案解析
答案解析
 有奖纠错
有奖纠错
