全一卷
1.已知函数 在区间
在区间 内为减函数,在区间
内为减函数,在区间 内为增函数.则a=________.
内为增函数.则a=________.
 在区间
在区间 内为减函数,在区间
内为减函数,在区间 内为增函数.则a=________.
内为增函数.则a=________.2.设A 、B 是两个集合,称(A ,B) 为一个“对子”.当 时,将
时,将 与
与 视为不同的对子.则满足条件
视为不同的对子.则满足条件 的不同的对子
的不同的对子 的个数为________.
的个数为________.
 时,将
时,将 与
与 视为不同的对子.则满足条件
视为不同的对子.则满足条件 的不同的对子
的不同的对子 的个数为________.
的个数为________.3.设函数 .若
.若 ,则你对函数
,则你对函数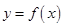 在区间
在区间 中零点存在情形的判断是________.
中零点存在情形的判断是________.
 .若
.若 ,则你对函数
,则你对函数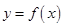 在区间
在区间 中零点存在情形的判断是________.
中零点存在情形的判断是________.4.已知椭圆 的两个焦点分别为
的两个焦点分别为 ,点
,点 满足
满足 .则
.则 的取值范围是________.
的取值范围是________.
 的两个焦点分别为
的两个焦点分别为 ,点
,点 满足
满足 .则
.则 的取值范围是________.
的取值范围是________.5.已知复数 满足
满足 (i为虚数单位),复数
(i为虚数单位),复数 的虚部为2.则
的虚部为2.则  为实数的条件是
为实数的条件是
________ .
 满足
满足 (i为虚数单位),复数
(i为虚数单位),复数 的虚部为2.则
的虚部为2.则  为实数的条件是
为实数的条件是
6.已知数列 满足递推关系式
满足递推关系式 且
且 为等差数列.则
为等差数列.则 的取值是________.
的取值是________.
 满足递推关系式
满足递推关系式 且
且 为等差数列.则
为等差数列.则 的取值是________.
的取值是________.7.过函数 的图像上一点的切线斜率为 k.则 k的取值范围是________.
的图像上一点的切线斜率为 k.则 k的取值范围是________.
 的图像上一点的切线斜率为 k.则 k的取值范围是________.
的图像上一点的切线斜率为 k.则 k的取值范围是________.8.已知平面内三点A、B、C满足 ,
, ,
, ,则
,则 的值为
的值为________ .
 ,
, ,
, ,则
,则 的值为
的值为9.若边长为4的正方形 沿
沿 折成
折成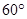 的二面角,则边
的二面角,则边 的中点与点
的中点与点 的距离为______.
的距离为______.
 沿
沿 折成
折成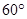 的二面角,则边
的二面角,则边 的中点与点
的中点与点 的距离为______.
的距离为______.10.有黑、自、黄筷子各 8 支,不用眼睛看任意地取出筷子,使得至少有两双筷子不同色.则至少要取出________ 支筷子才能做得到.
11.将抛物线的焦点所在的区域称为抛物线的内部.试问:在允许将抛物线平移或旋转的条件下,平面内2011 条抛物线的内部能否盖住整个平面? 请作出判断,并证明你的结论.
12.设 .证明:
.证明:
 .证明:
.证明:
13.(1)设实数 .证明:
.证明:
(2 )从编号为 的 l00张卡片中,每次随机地抽取一张,然后放回,用这种方式连续抽取 20 次,设抽得的20个号码互不相同的概率为 P .证明:
的 l00张卡片中,每次随机地抽取一张,然后放回,用这种方式连续抽取 20 次,设抽得的20个号码互不相同的概率为 P .证明: .
.
 .证明:
.证明:
(2 )从编号为
 的 l00张卡片中,每次随机地抽取一张,然后放回,用这种方式连续抽取 20 次,设抽得的20个号码互不相同的概率为 P .证明:
的 l00张卡片中,每次随机地抽取一张,然后放回,用这种方式连续抽取 20 次,设抽得的20个号码互不相同的概率为 P .证明: .
.14.已知由 的顶点A 引出的两条射线AX 、AY 分别与 BC 交于点 X、Y.证明:
的顶点A 引出的两条射线AX 、AY 分别与 BC 交于点 X、Y.证明: 成立的充要条件是
成立的充要条件是 .
.
 的顶点A 引出的两条射线AX 、AY 分别与 BC 交于点 X、Y.证明:
的顶点A 引出的两条射线AX 、AY 分别与 BC 交于点 X、Y.证明: 成立的充要条件是
成立的充要条件是 .
. 搜索
搜索
 难度系数:0.65
难度系数:0.65  答案解析
答案解析
 有奖纠错
有奖纠错
