全一卷
1.对任意实数 ,均有
,均有 .则实数
.则实数 的最小值为__________.
的最小值为__________.
 ,均有
,均有 .则实数
.则实数 的最小值为__________.
的最小值为__________.2.将五名大学生分配到某乡镇的三个村就职.若每个村至少一名,则不同的分配方案数为__________.
3.若 ,则
,则 __________.
__________.
 ,则
,则 __________.
__________.4.已知顶角为 的等腰三角形的底边长为
的等腰三角形的底边长为 ,腰长为
,腰长为 .则
.则 的值为__________.
的值为__________.
 的等腰三角形的底边长为
的等腰三角形的底边长为 ,腰长为
,腰长为 .则
.则 的值为__________.
的值为__________.5.设 ,
, ,
, 中的元素个数为_______
中的元素个数为_______
 ,
, ,
, 中的元素个数为_______
中的元素个数为_______6.已知点 在
在 所在的平面内,
所在的平面内, ,
, 为锐角,且
为锐角,且 ,
, ,
, .当
.当 取得最小值是,
取得最小值是,
__________ .
 在
在 所在的平面内,
所在的平面内, ,
, 为锐角,且
为锐角,且 ,
, ,
, .当
.当 取得最小值是,
取得最小值是,
7.已知正三棱锥 的底面的边长为6,侧棱长为
的底面的边长为6,侧棱长为 ,则该三棱锥的内切球的半径为__________.
,则该三棱锥的内切球的半径为__________.
 的底面的边长为6,侧棱长为
的底面的边长为6,侧棱长为 ,则该三棱锥的内切球的半径为__________.
,则该三棱锥的内切球的半径为__________.8.函数 的值域为__________.
的值域为__________.
 的值域为__________.
的值域为__________.9.已知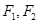 是椭圆
是椭圆 的两个焦点,A、B分别为该椭圆的左顶点、上顶点,点P在线段AB上,则
的两个焦点,A、B分别为该椭圆的左顶点、上顶点,点P在线段AB上,则 的取值范围是
的取值范围是________ .
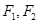 是椭圆
是椭圆 的两个焦点,A、B分别为该椭圆的左顶点、上顶点,点P在线段AB上,则
的两个焦点,A、B分别为该椭圆的左顶点、上顶点,点P在线段AB上,则 的取值范围是
的取值范围是10.使得 与
与 均是完全平方数的最大素数
均是完全平方数的最大素数 为__________.
为__________.
 与
与 均是完全平方数的最大素数
均是完全平方数的最大素数 为__________.
为__________.11.设平面点集 ,
, .若
.若 ,求
,求 的最小值.
的最小值.
 ,
, .若
.若 ,求
,求 的最小值.
的最小值.12.设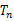 为数列
为数列 的前
的前 项之积,满足
项之积,满足
(1)求数列 的通项公式;
的通项公式;
(2)设 ,证明:
,证明: .
.
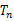 为数列
为数列 的前
的前 项之积,满足
项之积,满足
(1)求数列
 的通项公式;
的通项公式;(2)设
 ,证明:
,证明: .
.13.过直线 上一动点
上一动点 (
( 不在
不在 轴上)作抛物线
轴上)作抛物线 的两切线,
的两切线, 、
、 为切点,直线
为切点,直线 、
、 分别与
分别与 轴交于点
轴交于点 、
、 .证明:
.证明:
(1)直线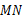 恒过一定点;
恒过一定点;
(2) 的外接圆恒过一定点,并求该圆半径的最小值.
的外接圆恒过一定点,并求该圆半径的最小值.
 上一动点
上一动点 (
( 不在
不在 轴上)作抛物线
轴上)作抛物线 的两切线,
的两切线, 、
、 为切点,直线
为切点,直线 、
、 分别与
分别与 轴交于点
轴交于点 、
、 .证明:
.证明:(1)直线
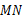 恒过一定点;
恒过一定点;(2)
 的外接圆恒过一定点,并求该圆半径的最小值.
的外接圆恒过一定点,并求该圆半径的最小值. 搜索
搜索
 难度系数:0.65
难度系数:0.65  答案解析
答案解析
 有奖纠错
有奖纠错
