全一卷
1.已知集合 ,
, .若集合
.若集合 ,则集合
,则集合 中元素的个数为______.
中元素的个数为______.
 ,
, .若集合
.若集合 ,则集合
,则集合 中元素的个数为______.
中元素的个数为______.2.已知函数 则
则 ______.
______.
 则
则 ______.
______.3.已知 ,
, .则
.则 的值为
的值为______ .
 ,
, .则
.则 的值为
的值为4.在三棱锥 中,已知
中,已知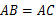 ,
, .则直线
.则直线 与
与 所成角的大小为______.
所成角的大小为______.
 中,已知
中,已知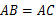 ,
, .则直线
.则直线 与
与 所成角的大小为______.
所成角的大小为______.5.如图,以双曲线 上一点
上一点 为圆心的圆与
为圆心的圆与 轴恰相切于双曲线的一个焦点
轴恰相切于双曲线的一个焦点 ,且与
,且与 轴交于
轴交于 、
、 两点.若
两点.若 为正三角形,则该双曲线的离心率为______.
为正三角形,则该双曲线的离心率为______.
 上一点
上一点 为圆心的圆与
为圆心的圆与 轴恰相切于双曲线的一个焦点
轴恰相切于双曲线的一个焦点 ,且与
,且与 轴交于
轴交于 、
、 两点.若
两点.若 为正三角形,则该双曲线的离心率为______.
为正三角形,则该双曲线的离心率为______.
6.设 为
为 的外心,且满足
的外心,且满足 .则
.则
______ .
 为
为 的外心,且满足
的外心,且满足 .则
.则
7.在 中,若
中,若 ,则
,则 的最小值为______.
的最小值为______.
 中,若
中,若 ,则
,则 的最小值为______.
的最小值为______.8.某人抛掷一枚硬币,出现正面向上和反面向上的概率均为 .构造数列
.构造数列 ,使
,使 记
记 .则
.则 ,且
,且 的概率为______(用最简分数作答).
的概率为______(用最简分数作答).
 .构造数列
.构造数列 ,使
,使 记
记 .则
.则 ,且
,且 的概率为______(用最简分数作答).
的概率为______(用最简分数作答).9.若正整数 、
、 满足
满足 ,则
,则 的值为______.
的值为______.
 、
、 满足
满足 ,则
,则 的值为______.
的值为______.10.设单调递增数列 的各项均为正整数,且
的各项均为正整数,且 ,
, .则
.则 ______。
______。
 的各项均为正整数,且
的各项均为正整数,且 ,
, .则
.则 ______。
______。11.设等比数列 的前
的前 项和为
项和为 ,且
,且 .
.
(1)求数列 的通项公式.
的通项公式.
(2)在 与
与 之间插入
之间插入 个实数,使这
个实数,使这 个数依次组成公差为
个数依次组成公差为 的等差数列.设数列
的等差数列.设数列 的前
的前 项和为
项和为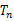 .证明:
.证明: .
.
 的前
的前 项和为
项和为 ,且
,且 .
.(1)求数列
 的通项公式.
的通项公式.(2)在
 与
与 之间插入
之间插入 个实数,使这
个实数,使这 个数依次组成公差为
个数依次组成公差为 的等差数列.设数列
的等差数列.设数列 的前
的前 项和为
项和为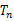 .证明:
.证明: .
.12.设 的内角
的内角 、
、 、
、 的对边分别为
的对边分别为 、
、 、
、 ,且满足
,且满足
 . ①
. ①
(1)证明: 为直角三角形;
为直角三角形;
(2)若 ,求
,求 面积的最大值.
面积的最大值.
 的内角
的内角 、
、 、
、 的对边分别为
的对边分别为 、
、 、
、 ,且满足
,且满足 . ①
. ①(1)证明:
 为直角三角形;
为直角三角形;(2)若
 ,求
,求 面积的最大值.
面积的最大值.13.如图,设 为锐角
为锐角 的垂心,过点
的垂心,过点 作
作 的垂线,与
的垂线,与 交于点
交于点 ,过点
,过点 作
作 的垂线,与
的垂线,与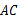 交于点
交于点 ,过点
,过点 作
作 的垂线,与直线
的垂线,与直线 交于点
交于点 .证明:
.证明: .
.
 为锐角
为锐角 的垂心,过点
的垂心,过点 作
作 的垂线,与
的垂线,与 交于点
交于点 ,过点
,过点 作
作 的垂线,与
的垂线,与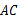 交于点
交于点 ,过点
,过点 作
作 的垂线,与直线
的垂线,与直线 交于点
交于点 .证明:
.证明: .
.
14.如图,在直角坐标系 中,
中, 与
与 轴的正半轴交于点
轴的正半轴交于点 ,
, 与
与 交于
交于 、
、 两点.
两点.

(1)求 的最小值;
的最小值;
(2)设 为
为 上异于
上异于 、
、 的任一点,直线
的任一点,直线 、
、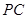 与
与 轴分别交于点
轴分别交于点 、
、 ,求
,求 的最大值.
的最大值.
 中,
中, 与
与 轴的正半轴交于点
轴的正半轴交于点 ,
, 与
与 交于
交于 、
、 两点.
两点.
(1)求
 的最小值;
的最小值;(2)设
 为
为 上异于
上异于 、
、 的任一点,直线
的任一点,直线 、
、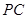 与
与 轴分别交于点
轴分别交于点 、
、 ,求
,求 的最大值.
的最大值.15.已知函数 ,
, .
.
(1)若对任意 ,恒有不等式
,恒有不等式 ,求
,求 的取值范围;
的取值范围;
(2)证明:对任意 ,有
,有 .
.
 ,
, .
.(1)若对任意
 ,恒有不等式
,恒有不等式 ,求
,求 的取值范围;
的取值范围;(2)证明:对任意
 ,有
,有 .
.16.设 表示不超过实数
表示不超过实数 的最大整数.已知
的最大整数.已知 .求
.求 .
.
 表示不超过实数
表示不超过实数 的最大整数.已知
的最大整数.已知 .求
.求 .
. 搜索
搜索
 难度系数:0.65
难度系数:0.65  答案解析
答案解析
 有奖纠错
有奖纠错
