搜索
全一卷
难度系数：0.65 
答案解析
有奖纠错
1．设
(
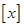表示不超过实数
的最大整数),集合
则集合A中元素的个数为
(
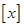表示不超过实数
的最大整数),集合
则集合A中元素的个数为| A．4 | B．6 | C．8 | D．12 |
2．已知
的三边长
成等比数列,边所对的角依次为
,且
.则
为
的三边长
成等比数列,边所对的角依次为
,且
.则
为A． | B． | C． | D． |
3．已知函数
.则
.则
| A．660 | B．664 | C．668 | D．672 |
4．已知数列
为由正整数组成的递增数列,且
若
,则
为由正整数组成的递增数列,且
若
,则
| A．102 | B．152 | C．212 | D．272 |
5．在长方体
中, 
.则异面直线
与
间的距离为
中, 
.则异面直线
与
间的距离为| A．1 | B． | C． | D． |
6．如图所示, 
分别为正六边形 
的对角线
的内分点,且
.若
三点共线,则
=
分别为正六边形 
的对角线
的内分点,且
.若
三点共线,则
=
A． | B． | C． | D． |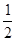
7．已知复数
在复平面内对应的点在第二象限,且
.则实数
的取值范围是______.
在复平面内对应的点在第二象限,且
.则实数
的取值范围是______.8．已知实数
满足
.则
______.
满足
.则
______.9．已知数列前
项和为
且对任意正整数
,均有
若
对任意的
恒成立,则实数
的最小值为______.
前
项和为
且对任意正整数
,均有
若
对任意的
恒成立,则实数
的最小值为______.10．在立方体中,点分别在线段
上(不包括线段的端点),且
.则
与
所成角的取值范围是______ .
中,点分别在线段
上(不包括线段的端点),且
.则
与
所成角的取值范围是11．一道数学竞赛题,甲、乙、丙三人单独解出此题的概率分别为
,其中, 
均为小于10的正整数.现甲、乙、丙同时独立解答此题若三人中恰有一人解出此题的概率为
,则三人均未解出此题的概率为______.
,其中, 
均为小于10的正整数.现甲、乙、丙同时独立解答此题若三人中恰有一人解出此题的概率为
,则三人均未解出此题的概率为______.12．设
为椭圆C的两个焦点,
为椭圆一条过点
的弦,且在
中,
.则
______.
为椭圆C的两个焦点,
为椭圆一条过点
的弦,且在
中,
.则
______.13．设实数
满足
,
.证明:
(1)
;
(2)
.
满足
,
.证明:(1)
;(2)
.14．如图, 
外接圆圆心为
,
,过点
作的垂线,垂足为
,作
分别与弧
、边
切于点
类似地,作
与弧
、边
相切.设
的半径分别为
、
,
的内切圆半径为
.证明: 
.
外接圆圆心为
,
,过点
作的垂线,垂足为
,作
分别与弧
、边
切于点
类似地,作
与弧
、边
相切.设
的半径分别为
、
,
的内切圆半径为
.证明: 
.
15．在数列
中,
,关于
的方程.
有唯一解.
(1)求数列的通项公式;
(2)设
,证明: 
(3)设
,求数列
的前n项和
中,
,关于
的方程.
有唯一解.(1)求数列
的通项公式;(2)设
,证明: 
(3)设
,求数列
的前n项和
16．在双曲线：
中，
、分别为双曲线的左、右两个焦点，
为双曲线上且在第一象限内的点，
的重心为
，内心为
.
（1）是否存在一点，使得
？
（2）设
为双曲线的左顶点，直线
过右焦点，与双曲线交于
、
两点.若
、
的斜率
、
满足
，求直线 的方程.
：
中，
、分别为双曲线的左、右两个焦点，
为双曲线上且在第一象限内的点，
的重心为
，内心为
.（1）是否存在一点
，使得
？（2）设
为双曲线的左顶点，直线
过右焦点，与双曲线交于
、
两点.若
、
的斜率
、
满足
，求直线 的方程.